Канонические уравнения в системе координат Оху
1. Эллипс задается уравнением:
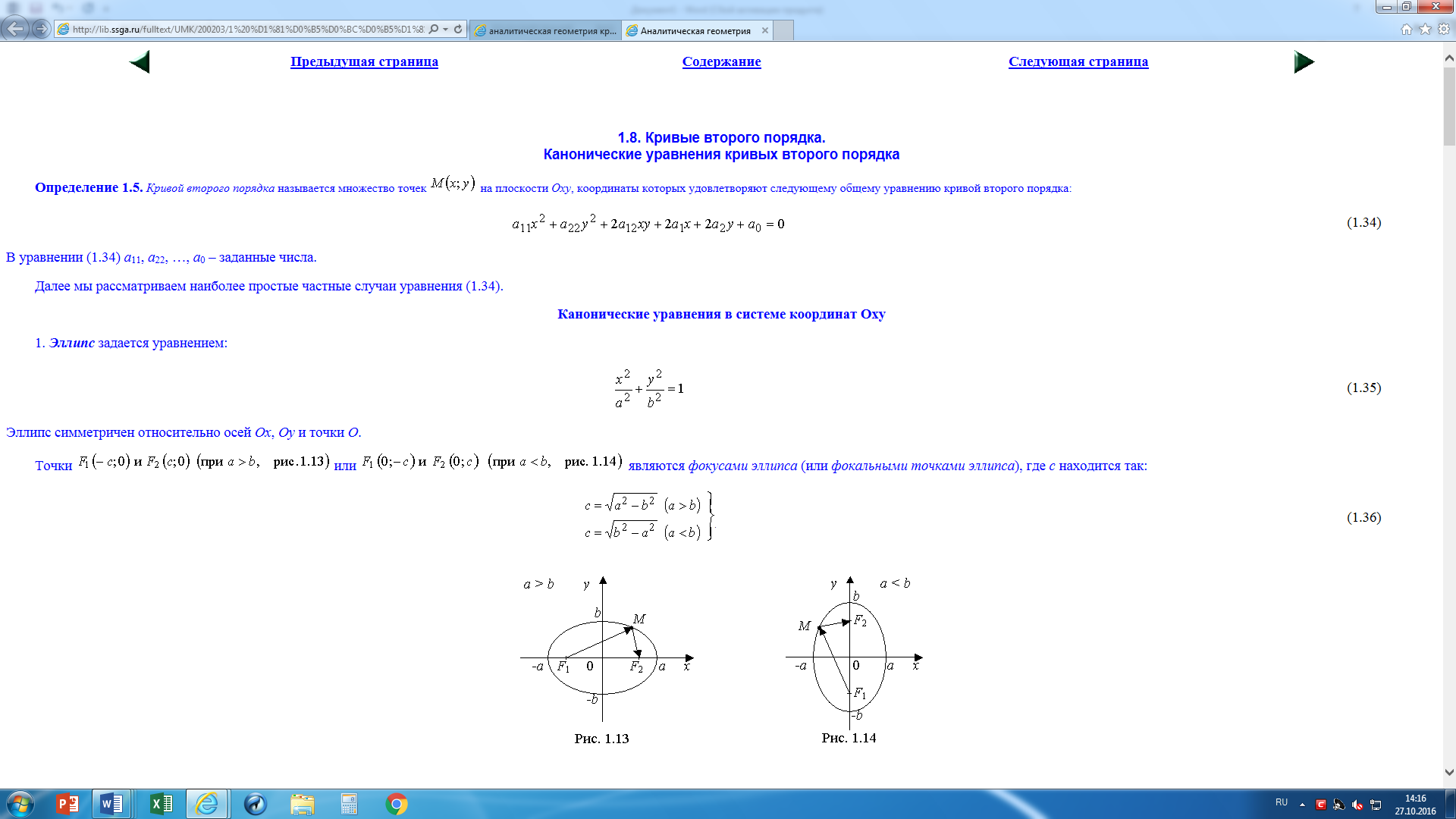
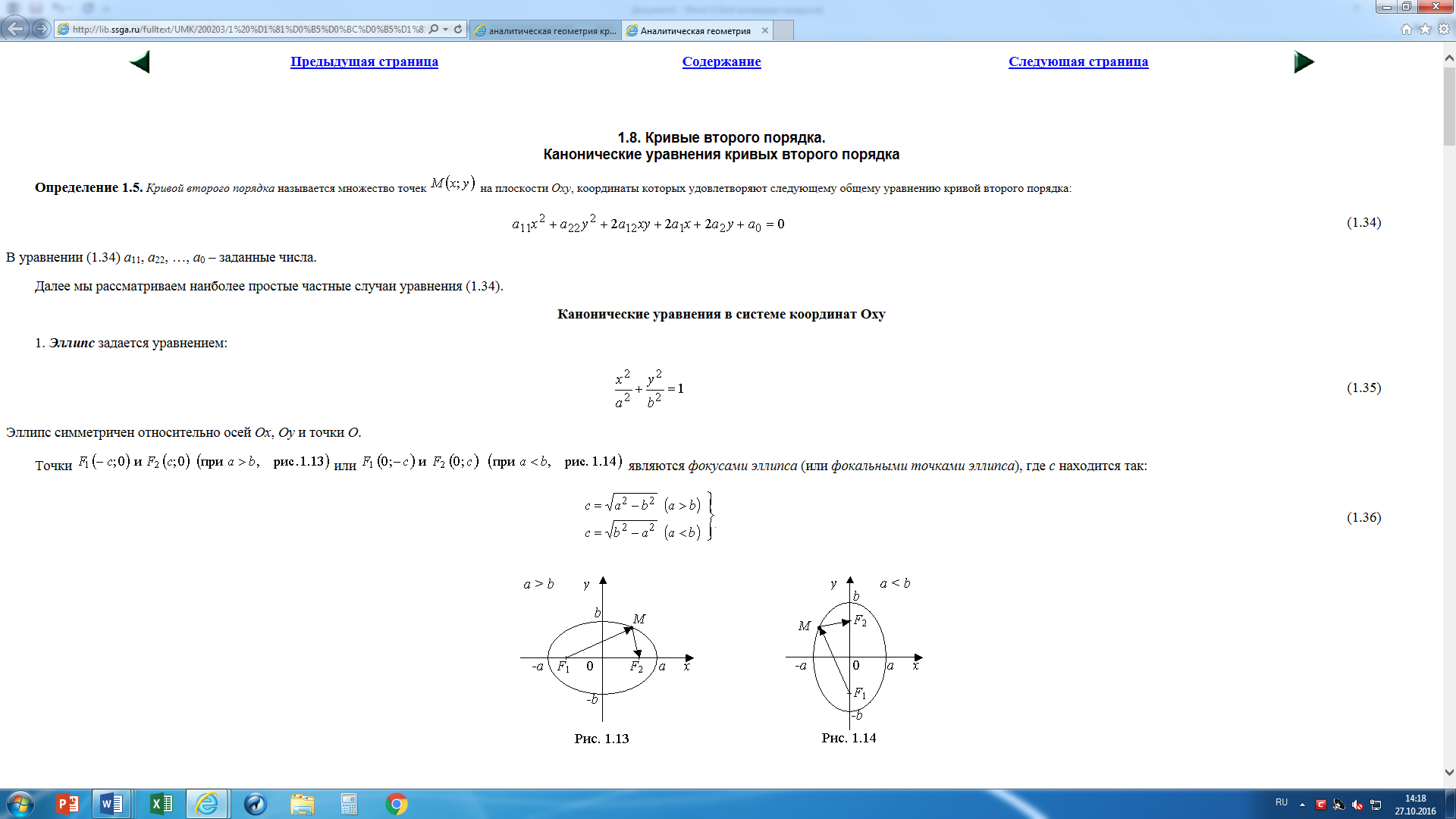
Эллипс симметричен относительно осей Ох, Оу и точки О.
Точки F1(-c;0) и F2 (с;0) при а>b (рис1) или F1(0;-c) и F2 (0;с) при а<b (рис 2) являются фокусами эллипса (или фокальными точками эллипса), где с находится так:
| . |
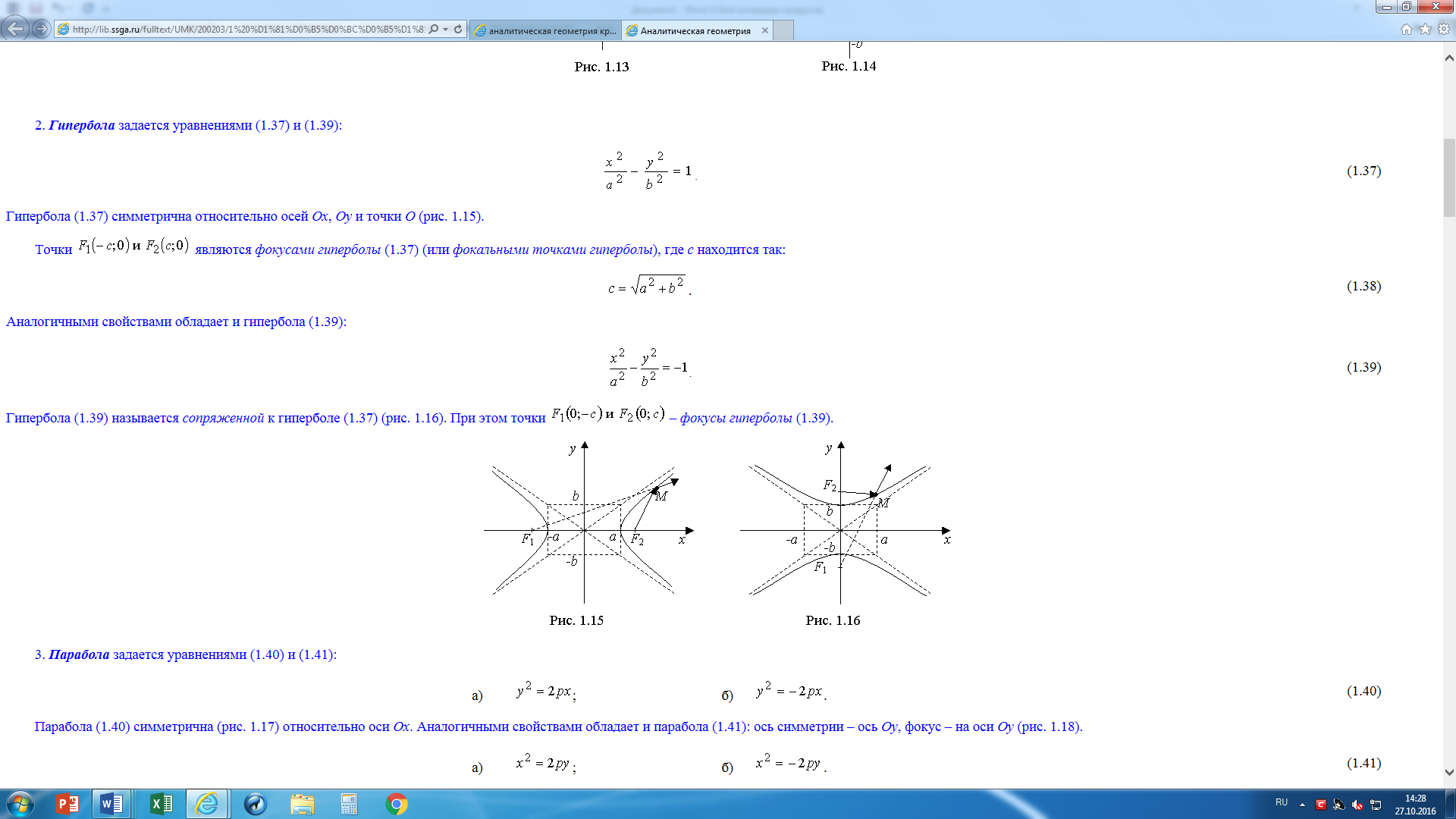
2. Гипербола задается уравнениями (4) и (6):
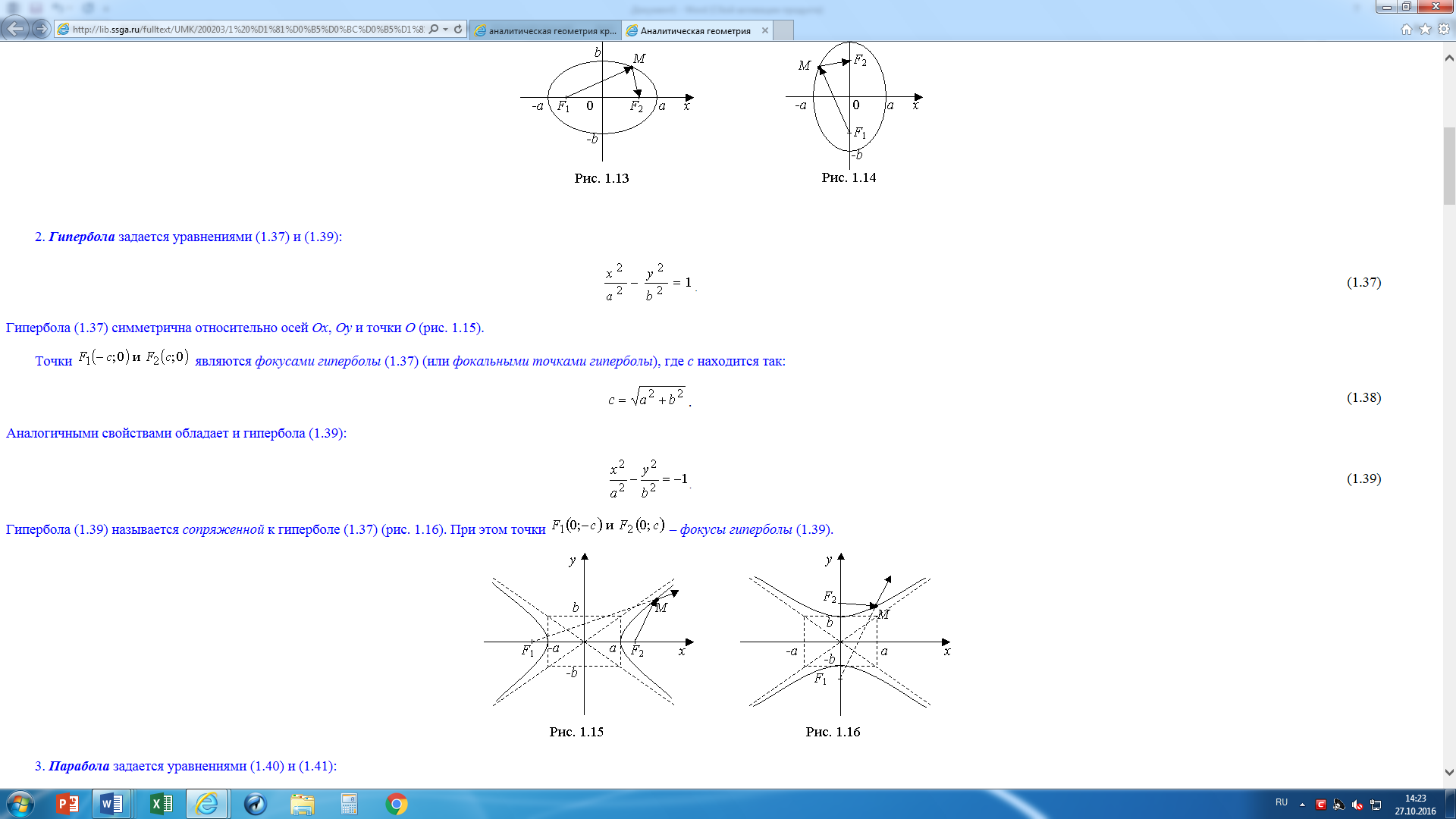
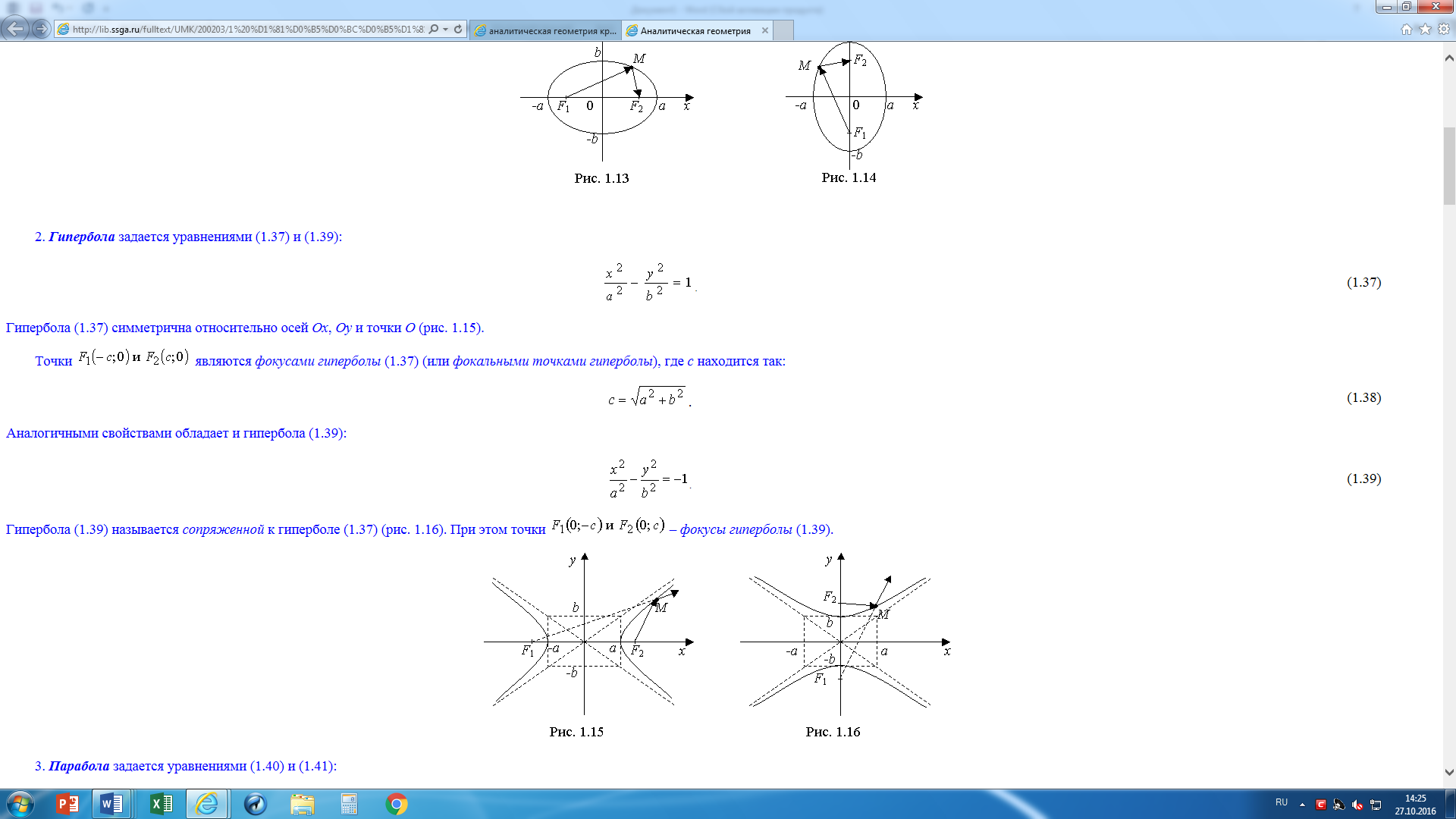
Гипербола (4) симметрична относительно осей Ох, Оу и точки О (рис. 3).
Точки F1(-c;0) и F2 (с;0) являются фокусами гиперболы (1.37) (или фокальными точками гиперболы), где с находится так:
Аналогичными свойствами обладает и гипербола (6):
 |
Гипербола (6) называется сопряженной к гиперболе (4) (4). При этом точки F1(0;-c) и F2 (0;с) – фокусы гиперболы (1.39).
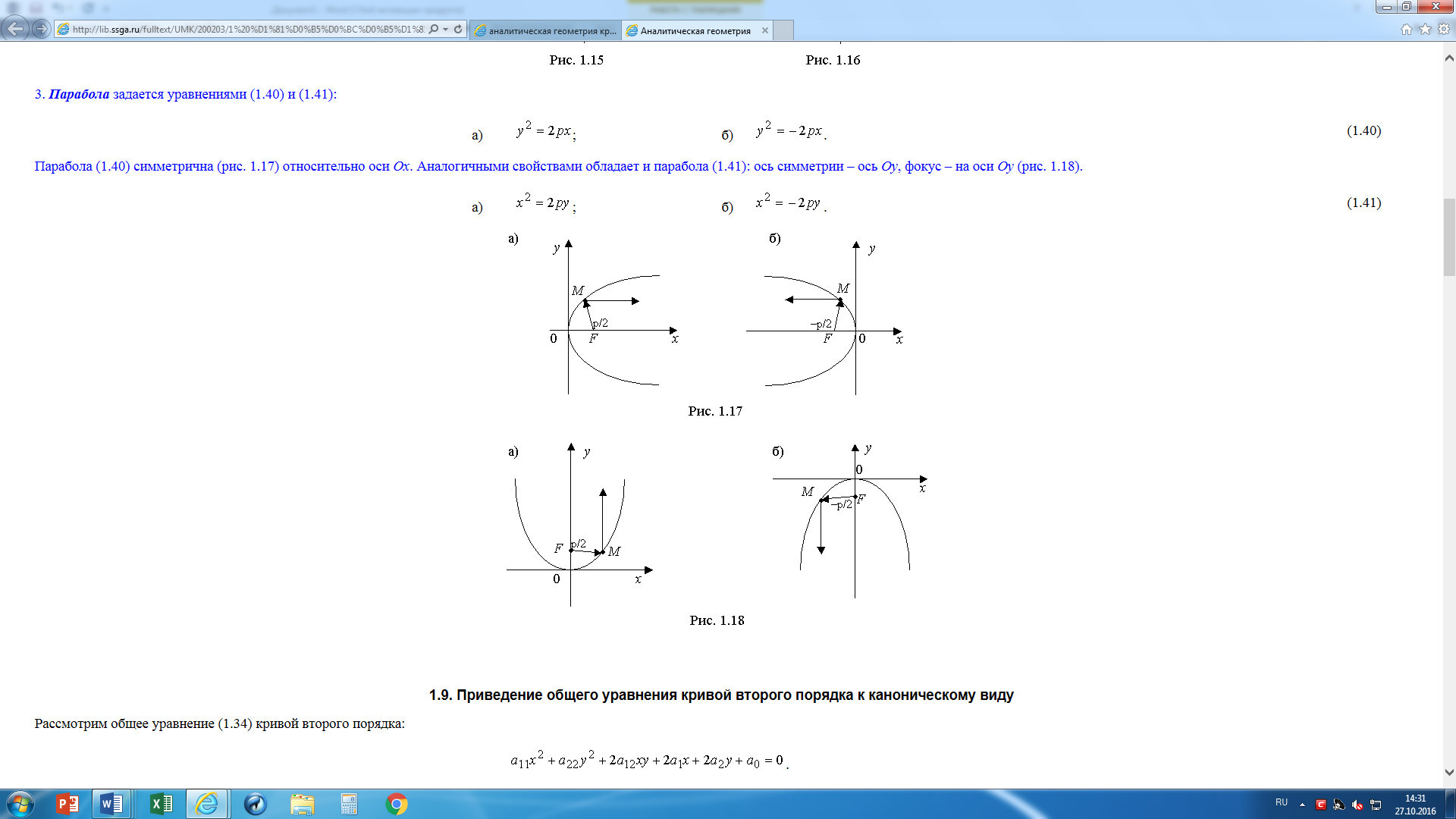
3. Парабола задается уравнениями (1.40) и (1.41):
| а)y2=2px; б) y2=-2px . | (7) |
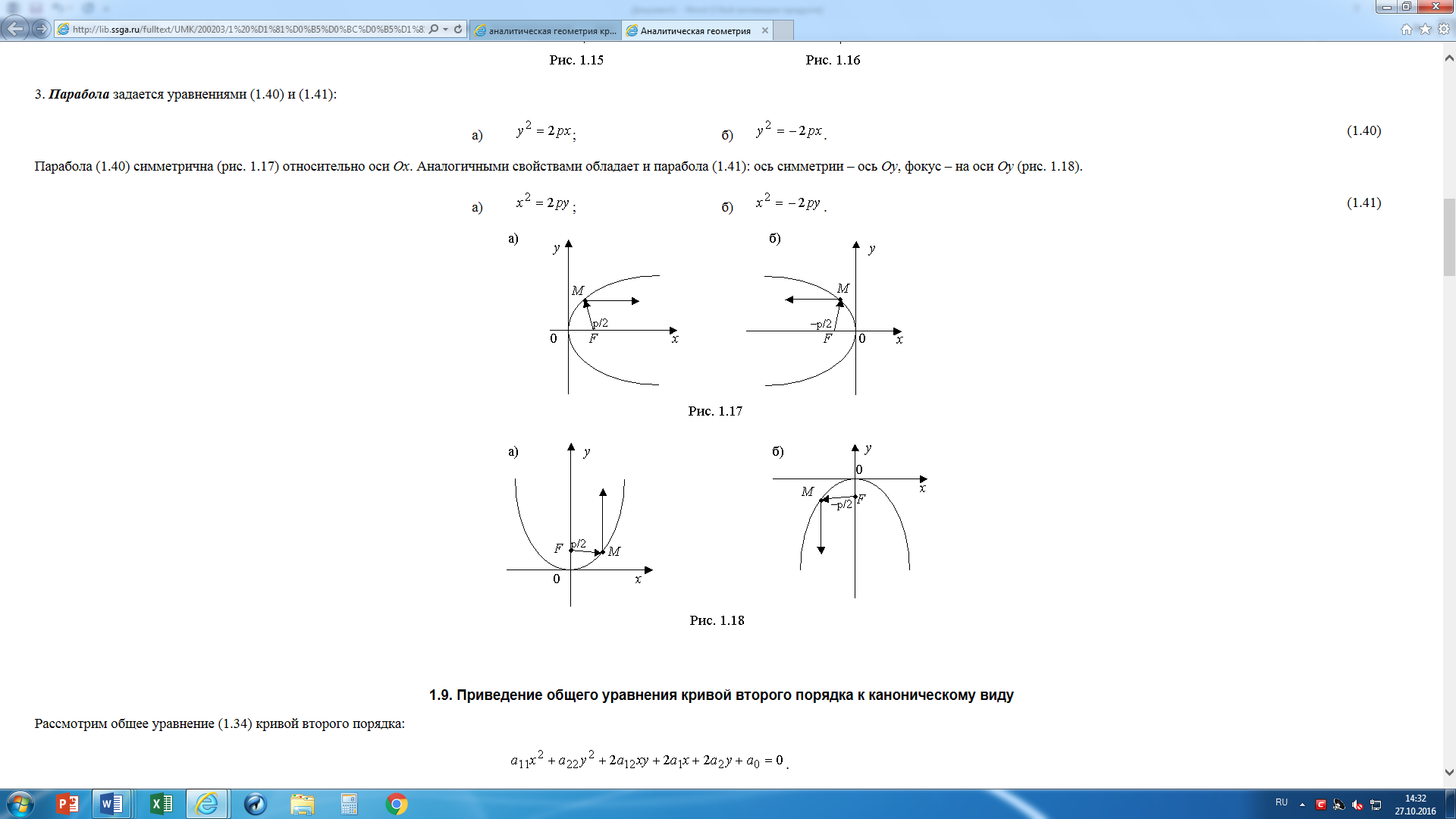
Парабола (7) симметрична (рис. 5) относительно оси Ох. Аналогичными свойствами обладает и парабола (8): ось симметрии – ось Оу, фокус – на оси Оу (рис. 6).
| а) x2=2py; б) x2=-2py . | (8) |
Методические указания
К выполнению контрольной работы
Контрольная работа должна быть выполнена в ученической тетради в клетку с полями. На обложке тетради указываются ФАМИЛИЯ, ИМЯ, ОТЧЕСТВО студента, КУРС, ФАКУЛЬТЕТ и СПЕЦИАЛЬНОСТЬ, по которой он обучается, НОМЕР и ВАРИАНТ контрольной работы.
Условия задач переписываются полностью, после чего приводится подробное решение со ссылками на использованные формулы, с аккуратными чертежами там, где они потребуются. В работе должны быть рассмотрены все задания. Работа, содержащая не все задания или задачи не своего варианта, не зачитывается.
Если работа содержит ошибки, она возвращается студенту с указанием допущенных ошибок. В этом случае студент должен сдать эту же работу повторно с исправлениями допущенных ошибок и дополнениями в конце ранее выполненной работы.
Контрольную работу следует сдать на заочное отделение не позже чем за неделю до начала экзаменационной сессии.
Задания контрольной работы
Задание 1:Решить систему линейных уравнений а)методом Гаусса, б) средствами матричного исчисления, в) по формулам Крамера
Вариант 1:
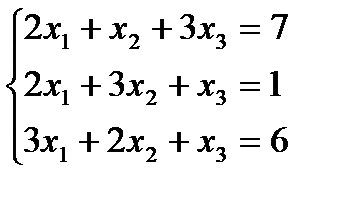
Вариант 2:
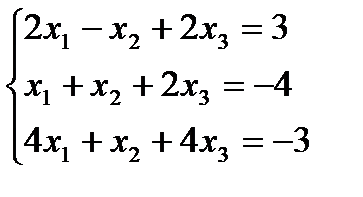
Вариант 3:
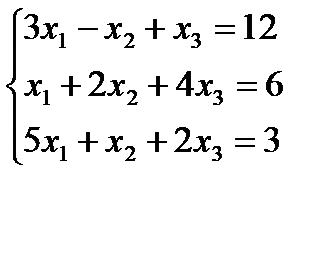
Вариант 4:
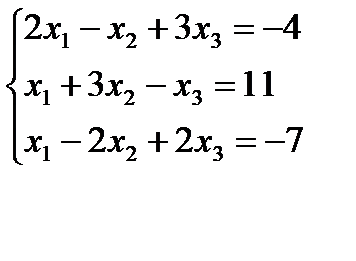
Вариант 5:
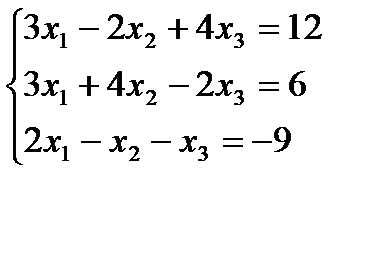
Вариант 6:
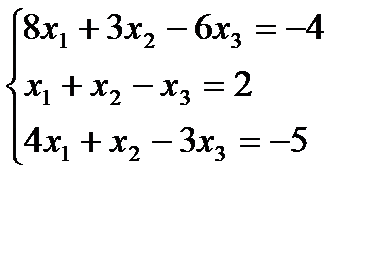
Вариант 7:
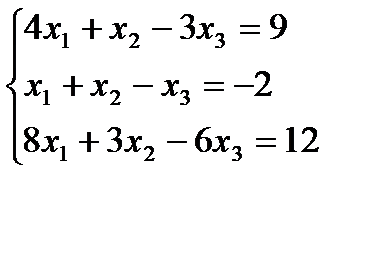
Вариант 8:
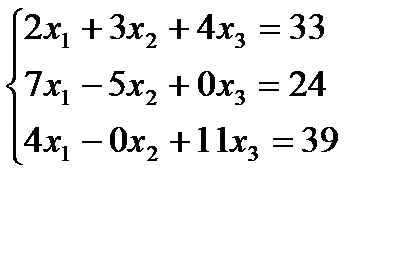
Вариант 9:
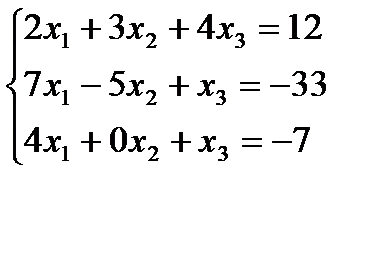
Вариант 10:
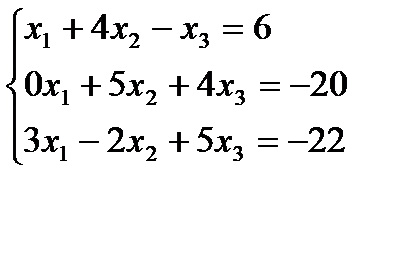
Вариант 11:
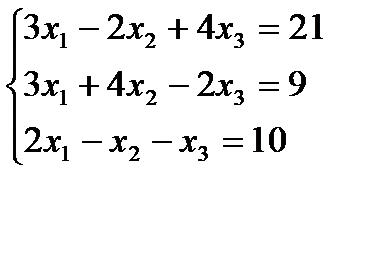
Вариант 12:
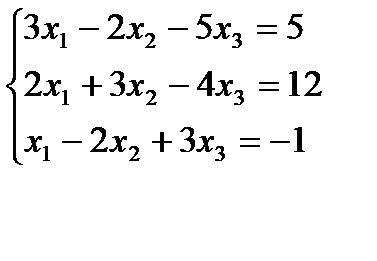
Вариант 13:
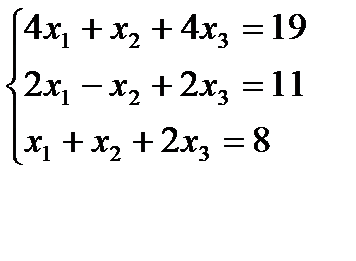
Вариант 14:
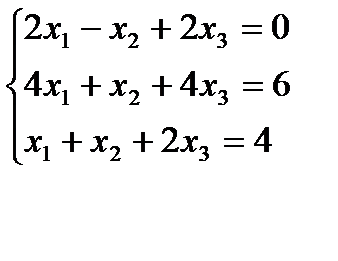
Вариант 15:
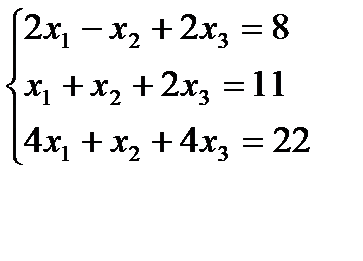
Вариант 16:
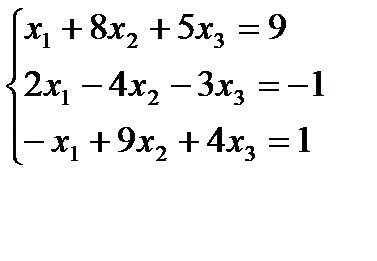
Вариант 17:
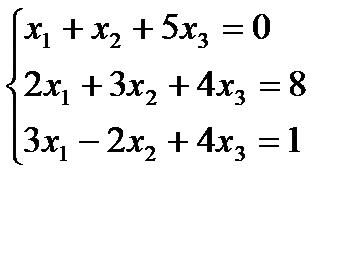
Вариант 18:
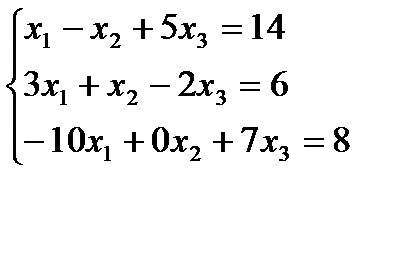
Вариант 19:
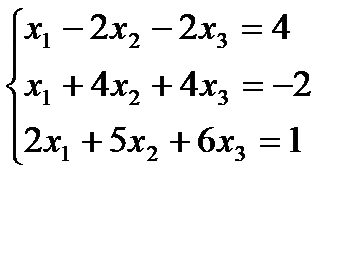
Вариант 20:
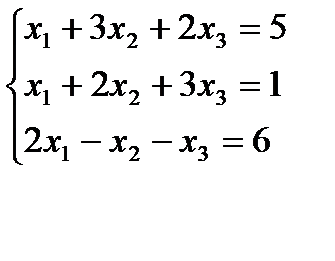
Задание 2:Вычислить пределы функций:
Вариант 1:
а) 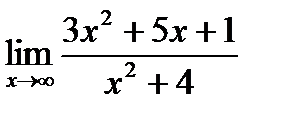 б)
б) 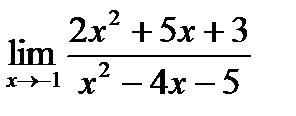 в)
в) 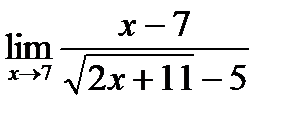
Вариант 2:
а) 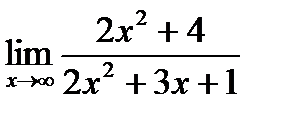 б)
б) 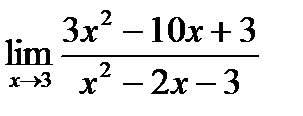 в)
в) 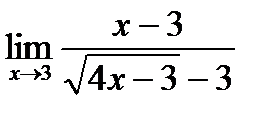
Вариант 3:
а) 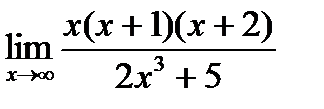 б)
б) 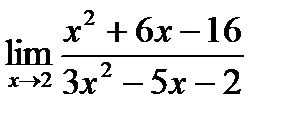 в)
в) 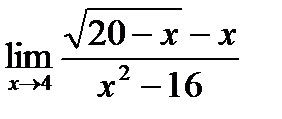
Вариант 4:
а) 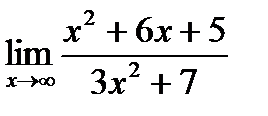 б)
б) 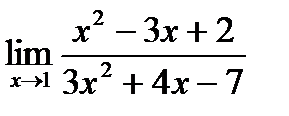 в)
в) 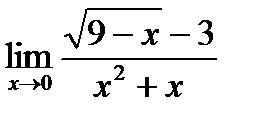
Вариант 5:
а) 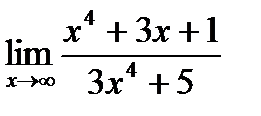 б)
б) 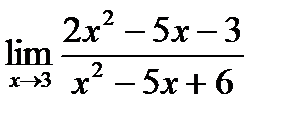 в)
в) 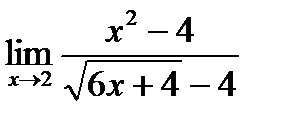
Вариант 6:
а) 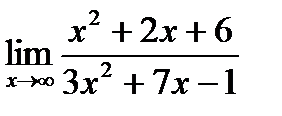 б)
б) 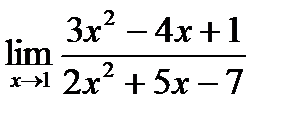 в)
в) 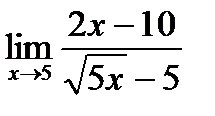
Вариант 7:
а) 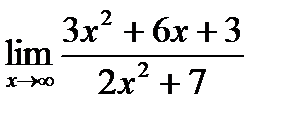 б)
б) 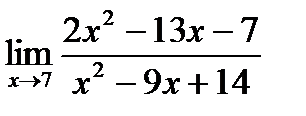 в)
в) 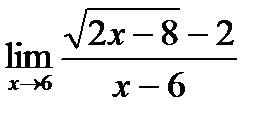
Вариант 8:
а) 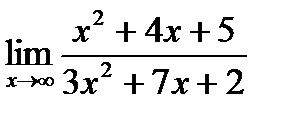 б)
б) 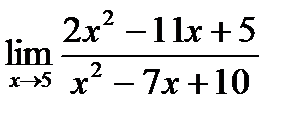 в)
в) 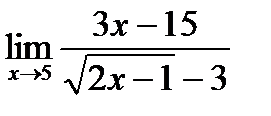
Вариант 9:
а) 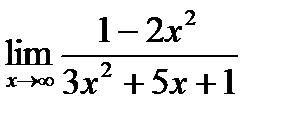 б)
б) 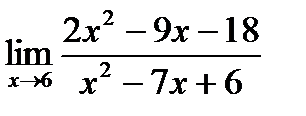 в)
в) 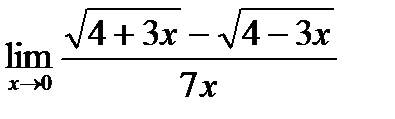
Вариант 10:
а) 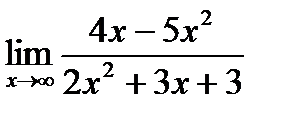 б)
б) 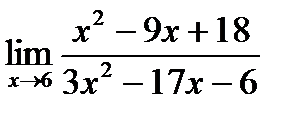 в)
в) 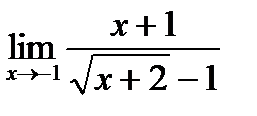
Вариант 11:
а) 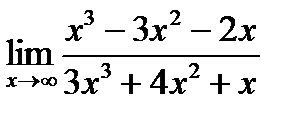 б)
б) 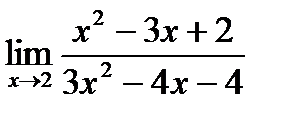 в)
в) 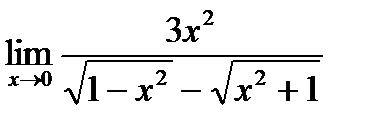
Вариант 12:
а) 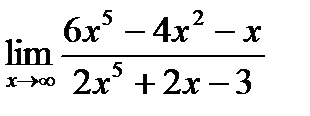 б)
б) 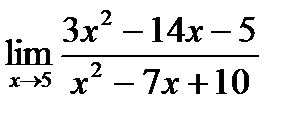 в)
в) 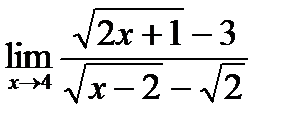
Вариант 13:
а) 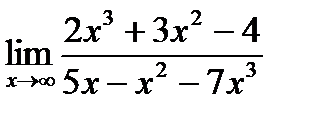 б)
б) 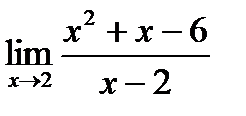 в)
в) 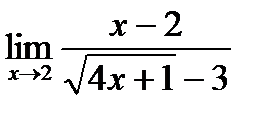
Вариант 14:
а) 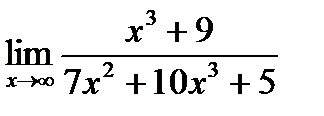 б)
б) 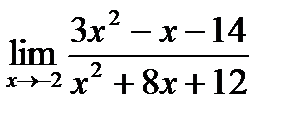 в)
в) 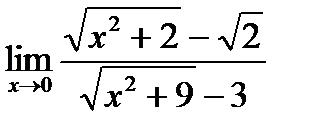
Вариант 15:
а) 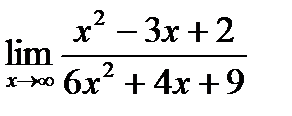 б)
б) 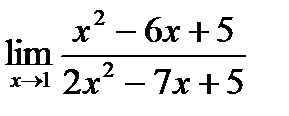 в)
в) 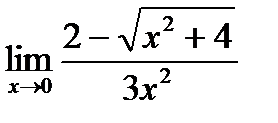
Вариант 16:
а) 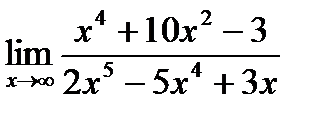 б)
б) 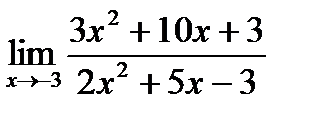 в)
в) 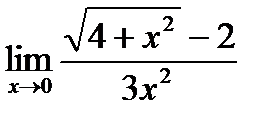
Вариант 17:
а) 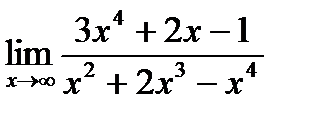 б)
б) 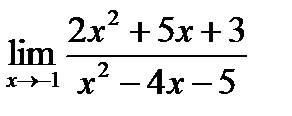 в)
в) 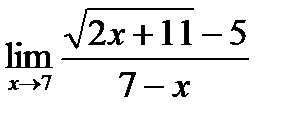
Вариант 18:
а) 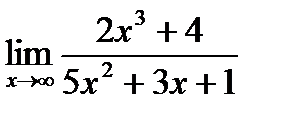 б)
б) 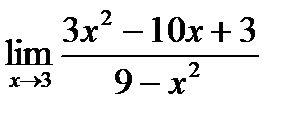 в)
в) 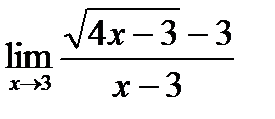
Вариант 19:
а) 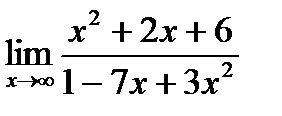 б)
б) 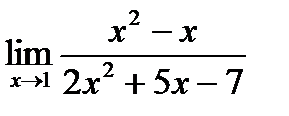 в)
в) 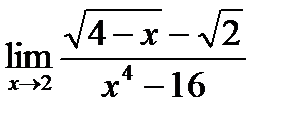
Вариант 20:
а) 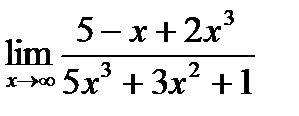 б)
б) 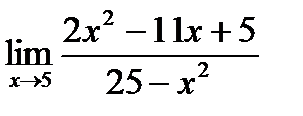 в)
в) 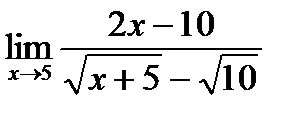
Задание 3.Найти производные функций.
В пункте в) найти вторую производную:
Вариант 1:
а) 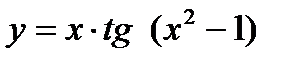 б)
б) 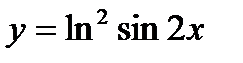 в)
в) 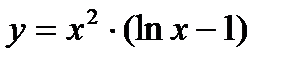
Вариант 2:
а) 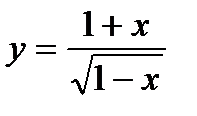 б)
б) 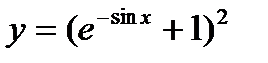 в)
в) 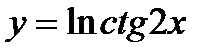
Вариант 3:
а) 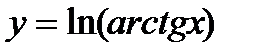 б)
б) 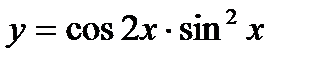 в)
в) 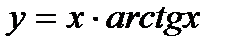
Вариант 4:
а) 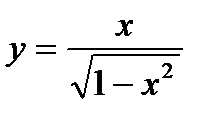 б)
б) 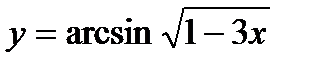 в)
в) 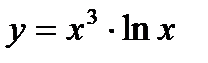
Вариант 5:
а) 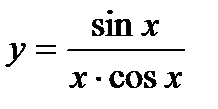 б)
б) 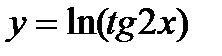 в)
в) 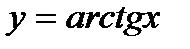
Вариант 6:
а) 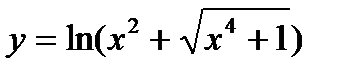 б)
б) 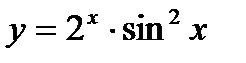 в)
в) 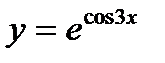
Вариант 7:
а) 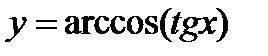 б)
б) 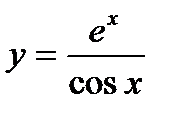 в)
в) 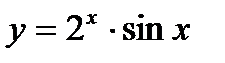
Вариант 8:
а) 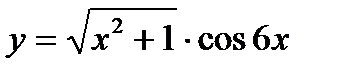 б)
б) 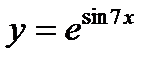 в)
в) 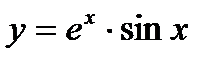
Вариант 9:
а) 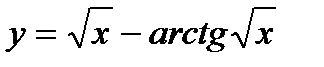 б)
б) 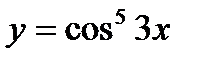 в)
в) 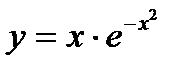
Вариант 10:
а) 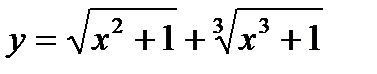 б)
б) 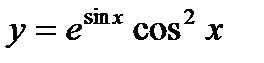 в)
в) 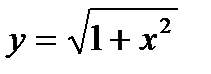
Вариант 11:
а) 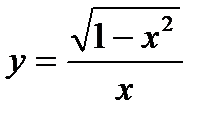 б)
б) 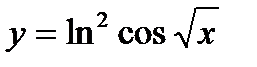 в)
в) 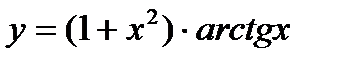
Вариант 12:
а) 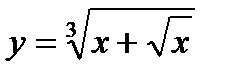 б)
б) 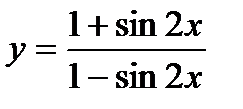 в)
в) 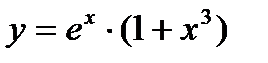
Вариант 13:
а) 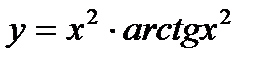 б)
б) 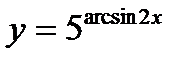 в)
в) 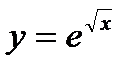
Вариант 14:
а) 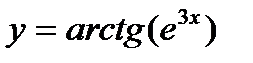 б)
б) 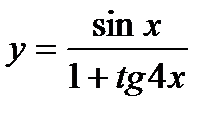 в)
в) 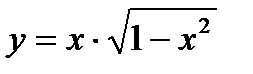
Вариант 15:
а) 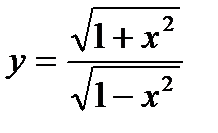 б)
б) 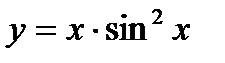 в)
в) 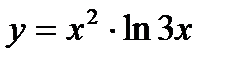
Вариант 16:
а) 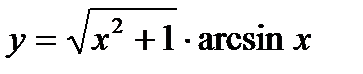 б)
б) 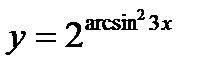 в)
в) 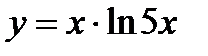
Вариант 17:
а) 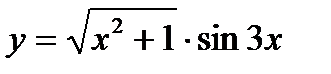 б)
б) 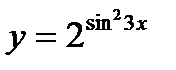 в)
в) 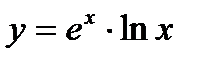
Вариант 18:
а) 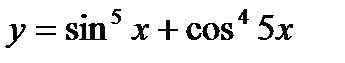 б)
б) 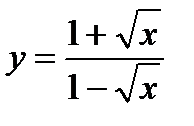 в)
в) 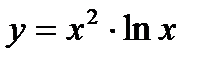
Вариант 19:
а) 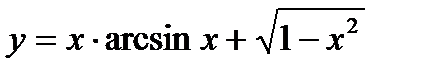 б)
б) 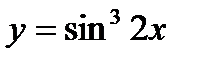 в)
в) 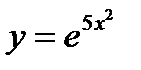
Вариант 20:
а) 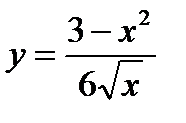 б)
б) 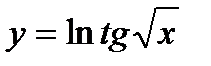 в)
в) 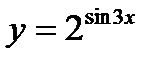
Задание 4: Исследовать функцию и построить ее график:
Вариант 1: 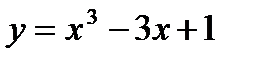 Вариант 2:
Вариант 2: 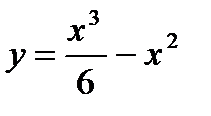
Вариант 3: 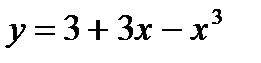 Вариант 4:
Вариант 4: 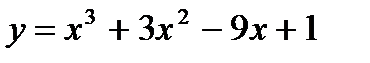
Вариант 5: 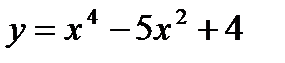 Вариант 6:
Вариант 6: 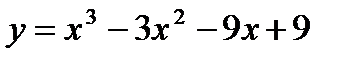
Вариант 7: 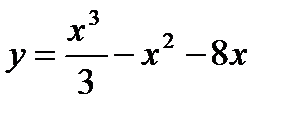 Вариант 8:
Вариант 8: 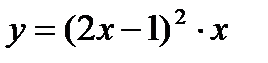
Вариант 9: 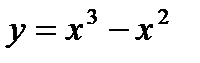 Вариант 10:
Вариант 10: 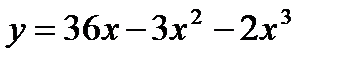
Вариант 11: 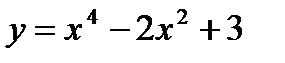 Вариант 12:
Вариант 12: 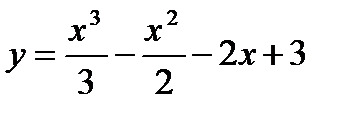
Вариант 13: 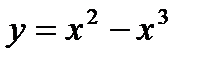 Вариант 14:
Вариант 14: 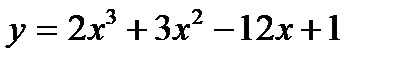
Вариант 15: 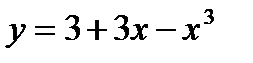 Вариант 16:
Вариант 16: 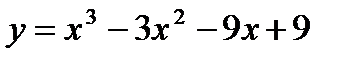
Вариант 17: 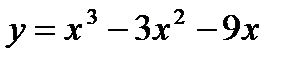 Вариант 18:
Вариант 18: 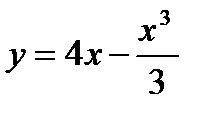
Вариант 19: 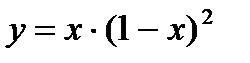 Вариант 20:
Вариант 20: 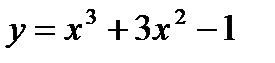
Задание 5: Найти неопределенные интегралы:
Вариант 1:
а) 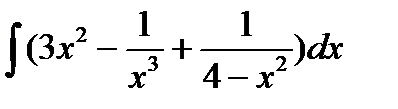 б)
б) 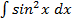
Вариант 2:
а) 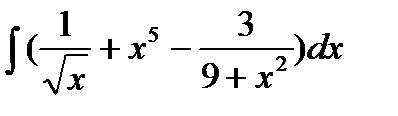 б)
б) 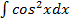
Вариант 3:
а) 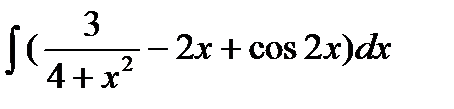 б)
б) 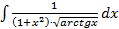
Вариант 4:
а) 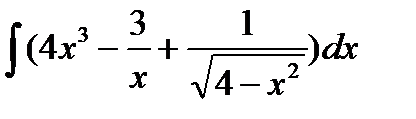 б)
б) 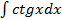
Вариант 5:
а) 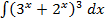 б)
б) 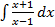
Вариант 6:
а) 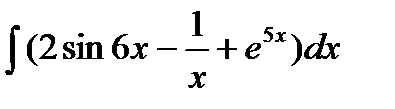 б)
б) 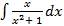
Вариант 7:
а) 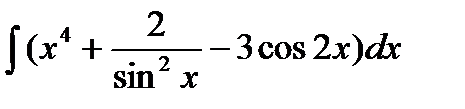 б)
б) 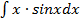
Вариант 8:
а) 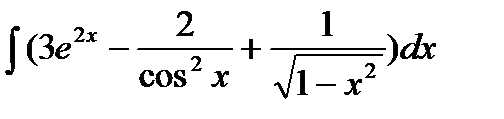 б)
б) 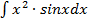
Вариант 9:
а) 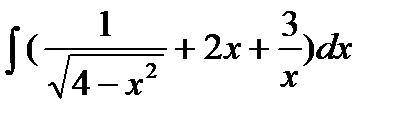 б)
б) 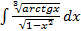
Вариант 10:
а) 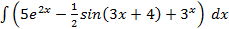 б)
б) 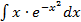
Вариант 11:
а) 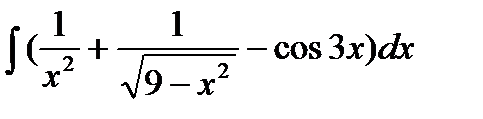 б)
б) 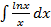
Вариант 12:
а) 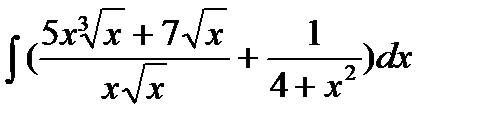 б)
б) 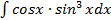
Вариант 13:
а) 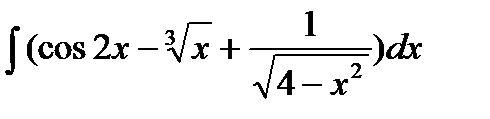 б)
б) 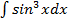
Вариант 14:
а) 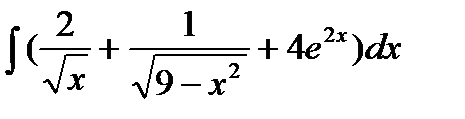 б)
б) 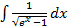
Вариант 15:
а) 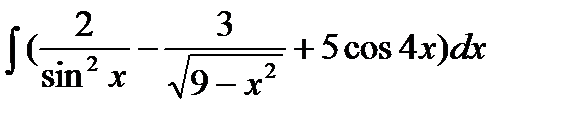 б)
б) 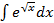
Вариант 16:
а) 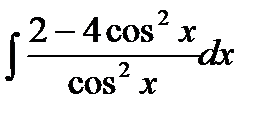 б)
б) 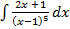
Вариант 17:
а) 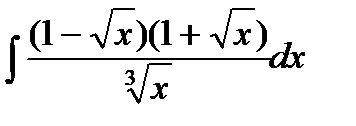 б)
б) 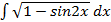
Вариант 18:
а) 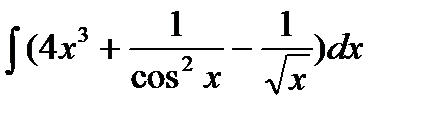 б)
б) 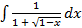
Вариант 19:
а) 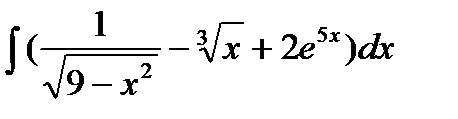 б)
б) 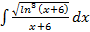
Вариант 20:
а) 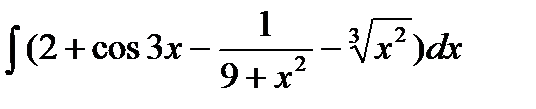 б)
б) 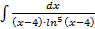
Задание 6: Найти площадь фигуры, ограниченной линиями. Сделать рисунок:
Вариант 1: 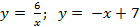
Вариант 2: 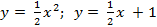
Вариант 3: 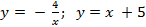
Вариант 4: 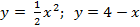
Вариант 5: 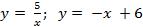
Вариант 6: 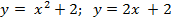
Вариант 7: 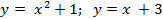
Вариант 8: 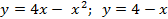
Вариант 9: 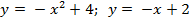
Вариант 10: 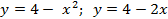
Вариант 11: 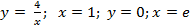
Вариант 12: 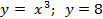
Вариант 13: 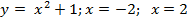
Вариант 14: 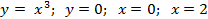
Вариант 15: 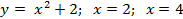
Вариант 16: 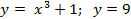
Вариант 17: 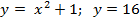
Вариант 18: 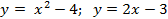
Вариант 19: 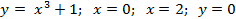
Вариант 20: 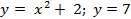
Задание 7: Найти частное решение дифференциального уравненияпервого порядка:
Вариант 1: 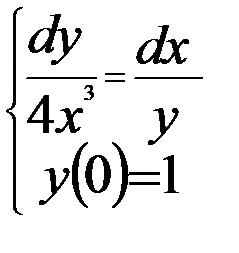 | Вариант 11: 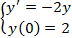 |
Вариант 2: 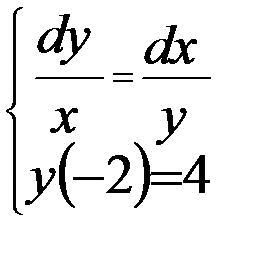 Вариант 3: Вариант 3: 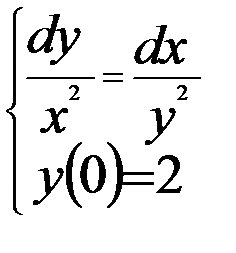 | Вариант 12: 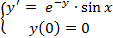 Вариант 13: Вариант 13: 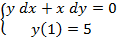 |
Вариант 4: 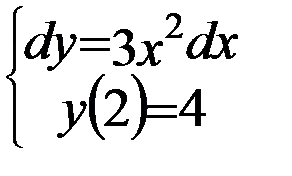 | Вариант 14: 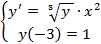 |
Вариант 5: 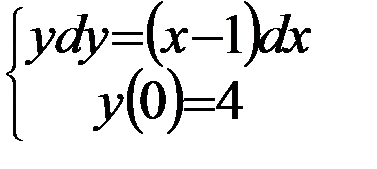 | Вариант 15: 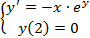 |
Вариант 6: 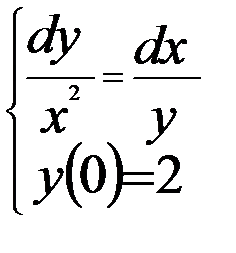 | Вариант 16: 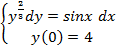 |
Вариант 7: 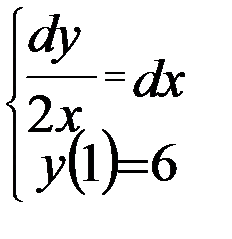 | Вариант 17: 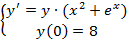 |
Вариант 8: 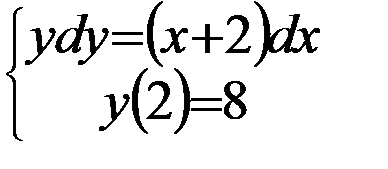 | Вариант 18: 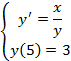 |
Вариант 9: 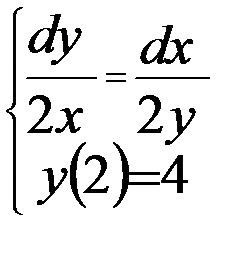 | Вариант 19: 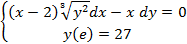 |
Вариант 10: 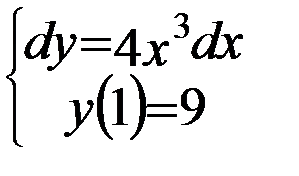 | Вариант 20: 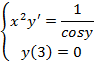 |
Задание 8:Вычислить приблизительно с точностью 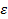 :
:
Вариант 1: 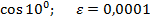
Вариант 2: 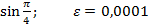
Вариант 3: 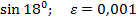
Вариант 4: 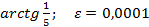
Вариант 5: 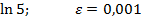
Вариант 6: 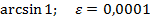
Вариант 7: 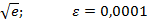
Вариант 8: 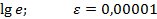
Вариант 9: 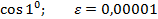
Вариант 10: 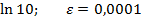
Вариант 11: 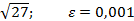
Вариант 12: 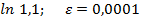
Вариант 13: 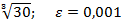
Вариант 14: 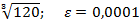
Вариант 15: 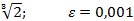
Вариант 16: 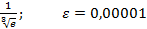
Вариант 17: 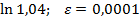
Вариант 18: 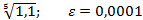
Вариант 19: 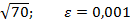
Вариант 20: 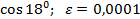
Задание 9:Дискретная случайная величина задана по закону. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Вариант 1:
| X | -1 | ||
| p | 0,2 | 0,1 | 0,15 |
Вариант 2:
| X | |||
| p | 0,3 | 0,1 | 0,15 |
Вариант 3:
| X | -1 | ||
| p | 0,4 | 0,2 | 0,12 |
Вариант 4:
| X | |||
| p | 0,2 | 0,5 | 0,15 |
Вариант 5:
| X | |||
| p | 0,2 | 0,6 | 0,14 |
Вариант 6:
| X | -1 | ||
| p | 0,3 | 0,6 | 0,15 |
Вариант 7:
| X | -1 | ||
| p | 0,7 | 0,1 | 0,12 |
Вариант 8:
| X | |||
| p | 0,7 | 0,4 | 0,11 |
Вариант 9:
| X | |||
| p | 0,7 | 0,3 | 0,14 |
Вариант 10:
| X | -1 | ||
| p | 0,8 | 0,5 | 0,15 |
Вариант 11:
| X | -1 | ||
| p | 0,3 | 0,2 | 0,17 |
Вариант 12:
| X | |||
| p | 0,2 | 0,6 | 0,14 |
Вариант 13:
| X | -1 | ||
| p | 0,3 | 0,5 | 0,15 |
Вариант 14:
| X | -2 | -1 | |
| p | 0,2 | 0,7 | 0,13 |
Вариант 15:
| X | |||
| p | 0,6 | 0,4 | 0,14 |
Вариант 16:
| X | -2 | -1 | |
| p | 0,2 | 0,14 | 0,15 |
Вариант 17:
| X | |||
| p | 0,1 | 0,9 | 0,8 |
Вариант 18:
| X | -1 | ||
| p | 0,3 | 0,5 | 0,9 |
Вариант 19:
| X | -1 | ||
| p | 0,2 | 0,11 | 0,25 |
Вариант 20:
| X | |||
| p | 0,3 | 0,21 | 0,4 |
Задание 10.
Вариант 1. Построить эллипс 9х2+25у2=225 Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис
Вариант 2. Установить, что уравнение
5х2+9у2-30х+18у+9=0 определяет эллипс, найти его центр C, полуоси, эксцентриситет и уравнения директрис.
Вариант 3. Построить гиперболу 16х2-9у2=144 Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Вариант 4.Установить, что уравнение 16х2-9у2-64х-54у-161=0 определяет гиперболу, найти ее центр C, полуоси, эксцентриситет, уравнения асимптот и директрис.
Вариант 5. Построить параболу у2=6х и найти ее параметры.
Вариант 6. Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси Ox и p=1/2.
Вариант 7. Установить, что уравнение y2 =4x−8 определяет параболу, найти координаты ее вершины A и величину параметра p.
Вариант 8.Вычислить фокальный параметр точки M параболы y2 =12x, если y(M)=6.
Вариант 9. Составить каноническое уравнение гиперболы, если расстояние между ее вершинами равно 8, а между фокусами -10. Сделать чертеж.
Вариант10.Найти уравнение параболы, которая симметрична относительно оси Ох, проходит через начало координат и точку М (1; -4)
Вариант 11. Построить эллипс 9х2+25у2=225 Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис
Вариант 12. Установить, что уравнение
5х2+9у2-30х+18у+9=0 определяет эллипс, найти его центр C, полуоси, эксцентриситет и уравнения директрис.
Вариант 13. Построить гиперболу 16х2-9у2=144 Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Вариант 14.Установить, что уравнение 16х2-9у2-64х-54у-161=0 определяет гиперболу, найти ее центр C, полуоси, эксцентриситет, уравнения асимптот и директрис.
Вариант 15. Построить параболу у2=6х и найти ее параметры.
Вариант 16. Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси Ox и p=1/2.
Вариант 17. Установить, что уравнение y2 =4x−8 определяет параболу, найти координаты ее вершины A и величину параметра p.
Вариант 18.Вычислить фокальный параметр точки M параболы y2 =12x, если y(M)=6.
Вариант 19. Составить каноническое уравнение гиперболы, если расстояние между ее вершинами равно 8, а между фокусами -10. Сделать чертеж.
Вариант 20. Найти уравнение параболы, которая симметрична относительно оси Ох, проходит через начало координат и точку М (1; -4)
