Минор. Алгебраическое дополнение.

Минором элемента a_ij матрицы n-го порядка называется определитель матрицы (n-1) - го порядка, полученный из матрицы A вычёркиванием i-й строки и j-го столбца, на пересечении которых находится выбранный элемент. ОбозначаетсяM_ij.
Так, если 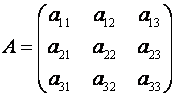, то M₁₁= 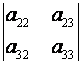, M₃₂= .

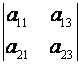Алгебраическим дополнением элемента a_ij матрицы n-го порядка называется его минор, взятый со знаком
(-1)^i+j:

A_ij=(-1)^i+j M_ij ,

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца

(i+j)−четное число, и отличается от минора знаком, когда (i+j)−нечетное число.

Например,A₂₃=(-1)²⁺³M₂₃=-M₂₃

Пример. Найти алгебраические дополнения всех элементов матрицы

Решение.

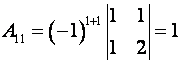
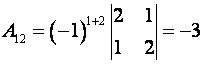
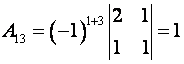
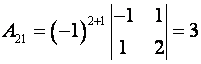
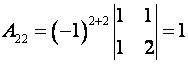
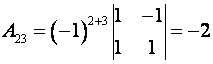
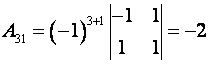
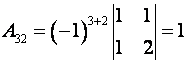
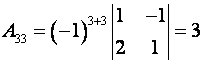
Свойства определителей

1. Если какой-либо ряд матрицы состоит из одних нулей, то ее определитель равен 0.

2. Если все элементы какого-либо ряда матрицы умножить на число, отличное от нуля, то ее определитель умножится на это число.

3. При транспонировании матрицы ее определитель не изменяется.

4.При перестановке двух параллельных рядов матрицы ее определитель меняет знак на противоположный.

5.Если квадратная матрица содержит два одинаковых ряда, то ее определитель равен 0.

6. Если все элементы некоторого ряда матрицы пропорциональны соответствующим элементам параллельного ряда, то ее определитель равен 0.

7. Сумма произведений элементов какого-либо ряда матрицы на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

8. Определитель матрицы не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, предварительно умноженные на одно и то же число.

9. Если элементы какого-либо ряда матрицы представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму соответствующих определителей.

10. Определитель произведения двух квадратных матриц равен произведению их определителей: |C|=|A|·|B|, где C=A·B, А и В − матрицы n-го порядка.

Системы линейных уравнений

Основные понятия и определения

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

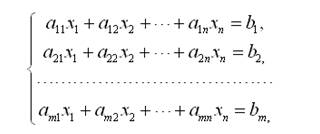
где числа a_ij, 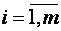, 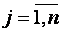называются коэффициентами системы, числа b_i– свободными членами. Подлежат нахождению числа x_n.

Такую систему удобно записывать в компактной матричной форме А·X=B.

Здесь А – матрица коэффициентов системы, называемая основной матрицей:

,

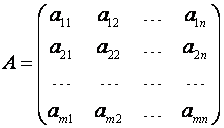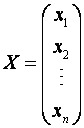– вектор–столбец из неизвестных x_j,

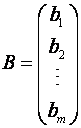– вектор–столбец из свободных членов b_i.

Если к основной матрице A добавить столбец свободных членов, получим расширенную матрицу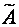

.

Решением системы называется п значений неизвестных x₁=c₁, x₂=c₂, …, x_n=c_n, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы – столбца .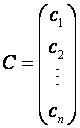

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти её общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.

Системой m линейных уравнений с n неизвестными называется система вида

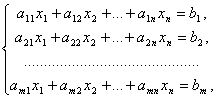
где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 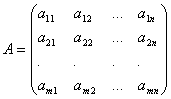, которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел с₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, 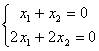. Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, 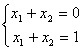, если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.