Задачи линейного программирования.
Графический метод.
Несмотря на то, что графический метод решения задач линейного программирования применяется только для задач с двумя искомыми переменными (или в случае трехмерного пространства с тремя), этот метод позволяет понять основную суть линейного программирования.
Задача 1.
Рассмотрим систему неравенств
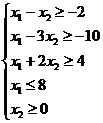 (1)
(1)
и линейную форму
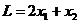 (2)
(2)
Найти минимум и максимум линейной формы (2) из области решений системы (1).
Решение.
Построим выпуклый многоугольник, заданный системой неравенств (1). Для этого построим прямоугольную систему координат х1ох2. Если в этой системе координат построить прямую ах1+bх2=с, то эта прямая разбивает плоскость х1ох2 на две полуплоскости, каждая из которых лежит по одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости удовлетворяют неравенству ах1+вх2≤с, а координаты точек, лежащих в другой полуплоскости, удовлетворяют неравенству ах1+вх2≥с. Построим в плоскости х1ох2 граничные прямые:
1) 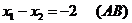 4)
4) 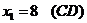
2) 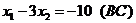 5)
5) 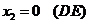
3) 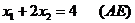
В результате получим пятиугольник АВСDЕ (рис. 2)
Значения х1 и х2 , удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника. Теперь задача сводится к тому, чтобы найти те значения х1 и х2 при которых линейная форма L (2) имеет минимум, и те значения х1 и х2 при которых линейная форма L достигает максимума. Из рис. 2 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т.е. все значения х1 и х2 больше или равны нулю.
|

Для каждой точки плоскости х1ох2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает фиксированное значение L1 , есть прямая 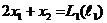 , которая перпендикулярна вектору
, которая перпендикулярна вектору 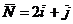 . Если прямую
. Если прямую 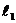 передвигать параллельно самой себе в положительном направлении вектора
передвигать параллельно самой себе в положительном направлении вектора 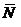 , то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую
, то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую 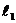 для того случая, когда L = 0, т.е. построим прямую
для того случая, когда L = 0, т.е. построим прямую 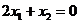 . Как видно из рис. 2, при передвижении прямой
. Как видно из рис. 2, при передвижении прямой 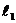 в положительном направлении вектора
в положительном направлении вектора 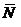 она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
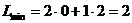 .
.
При дальнейшем передвижении прямой 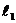 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 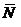 значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
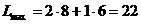 .
.
Задача 2.
Туристской фирме требуется не более 10 автобусов грузоподъёмностью 3 тонны и не более 8 автобусов грузоподъёмностью 5 тонн. Цена автобуса первой марки 20000 у.е., цена автобуса второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более 400000 у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной.
Решение.
Пусть приобретено х1 трёхтонных, х2 пятитонных автобусов, тогда заданные условия задачи можно записать так:
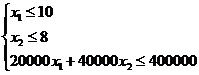 или
или 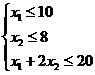 (1)
(1)
Линейная форма L (часто её называют целевой функцией) применительно к условиям нашей задачи имеет вид:
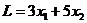 (2)
(2)
Требуется найти те значения х1 и х2, при которых L достигает максимального значения. По условию задачи 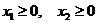 . Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
. Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
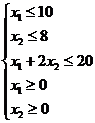 (3)
(3)
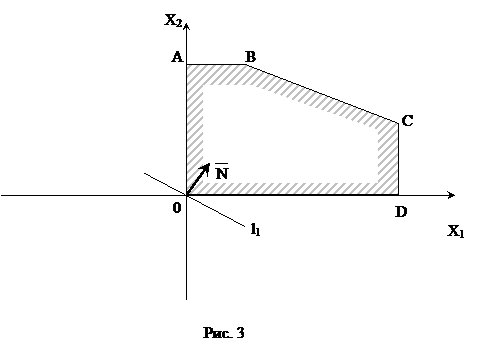

Затем построим вектор 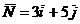 и прямую
и прямую 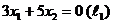 . Перемещая прямую
. Перемещая прямую 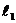 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 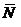 , установим, что L достигает максимального значения в точке С, для которой х1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. (
, установим, что L достигает максимального значения в точке С, для которой х1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. ( 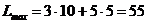 )
)
