Приведение масс и сил. Звено приведения

В динамике механизмов изучается их движение с учетом действующих сил.

Если все приложенные к звеньям силы известны, то можно определить закон движения какого-либо звена и механизма. Однако практическое

решение этой задачи оказывается весьма сложным. Поэтому, как правило, прибегают к отдельным частным решениям, применяя способы приближенного определения движения механизма. Для этого сложный многозвенный механизм заменяют его динамической моделью. Если механизм имеет только одну степень свободы, то в качестве модели механизма принимают одно условное звено. Так, для системы «электродвигатель - исполнительный механизм» выбирают в качестве начального звена вал электродвигателя. Закон движения условного звена должен полностью совпадать с законом движения начального звена. При этом угловые скорости начального и условного звеньев должны быть равны.

При решении задач кинематики и силового расчета механизмов с одной степенью свободы угловую скорость ω₁ ведущего кривошипа принимают постоянной. В действительности ω₁ даже при установившемся движении только в редких случаях остается постоянной. Обычно угловая скорость ω₁ периодически изменяется в зависимости от соотношения заданных сил, которые сами являются функциями различных параметров. Действительный закон движения ведущего звена определяют по методу Лагранжа с помощью звена приведения (динамической модели механизма), в качестве которого чаще всего выбирают ведущее звено - кривошип (или ползун). Если, например, задан шарнирный четырехзвенник с одной степенью свободы (рисунок 1.22, а), то его ведущий криво­шип 1 становится динамической моделью механизма (рисунок 1.22, б) после приведения к нему всех движущихся масс и всех заданных сил: движущих и сопротивления. Иначе говоря, для обращения кри­вошипа в звено приведения его момент инерции J_l должен быть за­менен приведенным моментом инерции J_п так, чтобы кинетическая энергия звена приведения Т_п стала равной кинетической энергии все­го механизма (Σ Т_i), т. е.

Т_п = J_пω₁² / 2 = Σ [J_Si ω_i² / 2 + m_iυ²_Si / 2]. (1.20)

Кроме того, мощности приведенных моментов сил сопротивлений Р_п.с и движущих сил Р_п.д должны быть равны сумме мощностей всех сил и моментов сил сопротивлений (F_сi, M_ci) и движущих (F_дi, М_дi), действующих на звенья механизма, т. е.

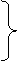Р_п.с= M_п.сω₁ = Σ N_ci = Σ [ M_ci ω_i + F_ci υ_ci cos α _ci ]; (1.21)

Р_п.д = M_п.дω₁ = Σ N_д.i= Σ [ М_д.iω_i + F_д.iυ_д..icos α _д._i ].

Рисунок 1.22

В выражениях (1.20) и (1.21) для i-го звена: υ_Si и ω_i - скорость центра масс и угловая скорость; m_i и J_Si - масса и момент инерции звена относительно оси, перпендикулярной плоскости вращения и проходящей через центр масс; M_ci и М_дi - моменты пар сил сопротив­лений и движущих; F_ci и υ_ci - сила сопротивлений и скорость точки C_i ее приложения; a_ci - угол, образуемый векторами F_ci и υ_ci (аналогично, α_дi – угол, образуемый векторами F_дi и υ_дi).

Приведение масс и сил может производиться не только к звену, но и к его произвольно взятой точке А (рисунок 1.22, в) - точке приве­дения. В этом случае в качестве обобщенной координаты выбирают перемещение S_a точки А по окружности. Массы всех подвижных звеньев заменяют приведенной массой т_п, сосредоточенной в точке А, а все заданные силы и моменты сил - приведенной силой F_п, при­ложенной к той же точке. Изложение материала данной главы про­изводится для случая, когда звеном приведения является ведущий кривошип. Если приведение масс и сил производится к точке, то формулы приведения и другие закономерности определяются ана­логично.

Из уравнения (1.20) находим приведенный момент инерции звена приведения:

J_п = 2Т_п/ ω²₁ = Σ [ J_Si (ω_i /ω₁)² + m_i (υ_Si /ω₁)² ]; (1.22)

он является функцией квадратов передаточных отношений. Послед­ние зависят от φ, поэтому и приведенный момент инерции является функцией обобщенной координаты J_п = J_п(φ).

Если ведущий кривошип 1 статически уравновешен (рисунок 1.22, б), то

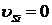и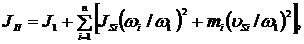

где J₁ = const - момент инер­ции кривошипа относительно оси его вращения.

Если в механизме имеются еще k звеньев, связанных с ве­дущим кривошипом постоянны­ми передаточными отношениями (ω_j/ω_ı = const)

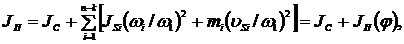, (1.23)

где 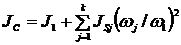− постоянная часть приведенного момента инерции, а J_п (φ) - переменная (рисунок 1.23).

Если все звенья механизма (например, зубчатого) вращаются вокруг своих центральных осей, то υ_S = 0, ω_j /ω_{1 =} const, J_п(φ) = 0 и J_п = J _c = const.

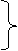Решением уравнений (1.21) относительно приведенных моментов сил сопротивлений и сил движущих находим следующие зависимости, выражающие закон передачи сил и моментов (без учета сил трения):

М_п.с = Σ[М_c.i(ω_i /ω₁) + F_c.i(V_ci /ω₁)cosα_ci]; (1.24)

М_п.д = Σ[М_д.i(ω_i /ω₁) + F_д.i(V_дi /ω₁)cosα_дi].

Рисунок 1.23