Ц)-перестановка из n-символов
Перестановкой из n-символов называется расположение этих символов в определённом порядке.
Говорят, что числа …i…..j…..образуют инверсию, если большее стоит левее меньшего (i>j).
Транспозиция – перемена местами 2х символов.
После транспозиции чётность меняется на нечётность и наоборот
Все n! перестановок из n символов можно расположить в таком порядке, что каждая последующая будет получаться из предыдущей 1 транспозицией.
Биективное соответствие множества, состоящего из n-символов, называется подстановкой.
Любая подстановка в записи может быть представлена 2мя перестановками, записанными друг под другом.
Каждая подстановка может быть записана n! способами.
ч)-четность\нечетность
Четностью перестановки называют общее число инверсий.
Если число инверсий четное, то перестановка четная, если это число нечетное, то перестановка нечетная.
Щ)-общее определение детерминанта.
Определителем (детерминантом) порядка n (квадратная матрица порядка n) называется число, равное алгебраической сумме n! слагаемых, каждое из которых представляет из себя произведения n-членов определителя, взятой по 1 и только по 1, взятое из каждой его строки и каждого столбца. При этом слагаемое берётся со знаком +, если подстановка, составленная из номеров строк и столбцов, входящих в данное произведение членов, чётная и со знаком -, если подстановка нечётная.
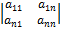 =
= 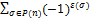
Ы)-свойства определителей
1- Определитель не меняется при транспозиции.
Замечание: Любое свойство для строк справедливо и для столбцов
2- Определитель содержащий строку из одних нулей, сам равен нулю
3- Если какую-либо строку определителя умножить на некоторое число, то и сам определитель умножается на это число.
4- Если поменять местами 2-ую строку, то определитель изменит знак на противоположный.
5- Если в определителе изменяются 2-е одинаковые строки, то он равен нулю.
6- Если в определителе имеются пропорциональные строки, то он равен нулю.
7- Если в определителе какая-либо строка представляет из себя сумму некоторых 2х пропорциональных матриц строк, тогда определитель равен сумме 2х определителей, у каждого из которых все строки кроме упомянутой те же самые, что и в исходном определителе.
8- Если к какой-либо строке определит любую другую его строку, предварительно умноженное на любое число, то определитель не изменится.
2.Геометрические векторы:
а)-свойства
1)  +
+  +
+ 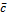 =
=  + (
+ (  +
+ 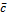 )- Ассоциативность сложения
)- Ассоциативность сложения
2) 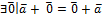 =
= 
3) 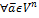 (n=0,1,2,3)
(n=0,1,2,3) 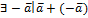 =
= 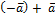 =0
=0
1-4 это абилева группа или коммутативная
4)  +
+  =
=  +
+  - Коммутативность сложения
- Коммутативность сложения
5) 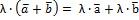 - Дистрибутивность умножения на число относительно сложения векторов
- Дистрибутивность умножения на число относительно сложения векторов
6) 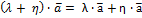 - Дистрибутивность умножения на число относительно сложения чисел
- Дистрибутивность умножения на число относительно сложения чисел
7) 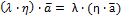 - Ассоциативность умножения на число
- Ассоциативность умножения на число
8) 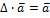
1-8 имеют место для любых  ,
,  ,
, 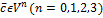
б)-линейные комбинации
Линейная комбинация – вектор  равен сумме произведений
равен сумме произведений 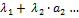
Вектор b = ∑mi=1λiai = λ1a1 + … + λmamназыв. линейной комбинацией векторов системы Am, а числа λ1, …, λmназыв. коэффиц. данной линейной комбинации.
Линейные комбинации называется тривиальной, если все ее коэффициенты = 0
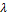 1 =
1 = 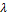 2 = ... +
2 = ... + 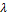 m = 0
m = 0
в)-зависимость(независимость)
Системы векторов Ам называется линейно зависимой, если сущ-ет нетривиальная линейная комбинация ее векторов = 0. В противном случае система Ам называется линейно-независимой.
Система Ам называется линейно независимой, если равенство 0 ее линейной комбинации возможно, только в тривиальном варианте.
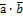 , b = -
, b = - 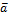 ,
, 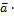 (-
(- 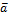 ) = 0 (комбинация не тривиальна, но она равна 0)
) = 0 (комбинация не тривиальна, но она равна 0)
Система Аm линейно зависима тогда и только тогда, когда один из векторов этой системы линейно выражается через остальные векторы этой же системы.
Система Am линейно независима тогда и только тогда, когда всякий вектор линейно выражающийся через нее единственен.
г)-критерии линейной независимости(док-во)
1) необходимость лин. зав. Пусть Am – лин-зав, т. е. $лин. нетрив. комб. ∑mi=1λiai=Ō λioaio + ∑mi=1(i≠io)λiai=Ō=>aio=∑mi=1(i≠io)μiai μi=–λi/λio 2) достаточность. Пусть вектор aioÎAm ∑mi=1λiai–1*aio= Ō Критерий лин. незав.: система векторов Amлин-незав. óякий вектор, линейно через нее выражающийся выражается через нее единственным способом. Док-во: 1) необходимость. Пусть Amлин-незав. a=∑mi=1λiai Пусть a=∑mi=1μiaia=∑mi=1(λi– μi)ai (λi– μi = γi) ∑mi=1 γiai= Ō => γi=0, т.е. λi= μi 2) достаточность. Пусть любой вектор, линейно-выражающийся через Am, т.е. такой, что a=∑mi=1λiai единств.образом. Ō=∑mi=1ηiai при ηi = 0 ∑mi=1λiai=Ō =>λi= μi =0
д)-базисы
Система векторов AmÌV называется полной, если всякий aÎV линейно выражается через векторы этой системы a=∑mi=1λiai.
Упорядоченная система векторов An=(a1, …,an) называется базисом векторного пространства V, если An – лин. незав. и полная.
1) Тривиальное пространство, сост. из Ō не имеет базиса.
2) Базис векторов на прямой – это любая система, сост. из одного ненулевого вектора.
3) Любая пара неколлинеарных векторов на плоскости образует базис.
4) Любая тройка некомпланарных векторов образует базис в пространстве.
Теорема. Если сущ. конечный базис An, n≠0 в векторном пространстве V, то любые два базиса состоят из одного и того же числа векторов.
Е)-размерности
Размерностью векторного пространства называется число векторов его базиса. (это опр. и теория формируются при условии. что выполняется аксиома размерности).
Аналитическая геометрия
а)-ориентация базиса
Пnn=0, 1, 2, 3
П0 – точка
П1 – прямая
П2 – плоскость
П3 – пространство
Vn – множество векторов на Пn
Vn – векторное пространство
(Пn,Vn) – аффинное пространство
dimVn=n
V1 – прямая линия
Говорят, что 2 базиса на прямой ( 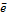 и
и 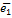 ) имеют одинаковую ориентацию, если коэффициент пропорциональности (
) имеют одинаковую ориентацию, если коэффициент пропорциональности ( 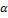 ) между ними больше нуля, в противном случае они имеют противоположную ориентацию.
) между ними больше нуля, в противном случае они имеют противоположную ориентацию.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Упорядоченная тройка некомпланарных векторов называется правой, если ее векторы расположены в том же порядке что и 3 пальца правой руки.
б)-декартовые координаты
в)-аффинные системы координат
Аффинная система координат (АСК) в Пn называется пара, состоящая из точки О и базиса 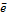 (О,
(О, 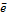 ) векторного пространства Vn.
) векторного пространства Vn.
Любой вектор в аффинном пространстве называется радиус-вектором (аффинной прямой).
Векторное или аффинное пространство, в котором введено скалярное произведение, является Евклидовым пространством.
г)-координаты точки
д)-прямоугольная Декарта
