Метод прогонки для решения систем линейных алгебраических уравнений.

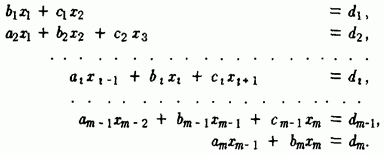
Преобразуем первое уравнение системы к виду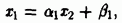

Подставим полученное выражение во второе уравнение системы:

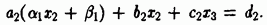
Преобразуем это уравнение к виду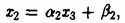

Выражение подставляем в третье уравнение системы и т. д. Далее уравнение системы преобразуется к виду 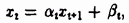. На следующем шаге подстановка в последнее уравнение выражения дает

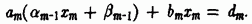
Отсюда можно определить значение

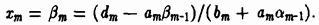
Уточнение решения системы линейных алгебраических уравнений.

Определение возможной ошибки решения системы линейных алгебраических уравнений.

Системы однородных линейных уравнений. Методы их решения.

Собственные значения и собственные векторы матриц.

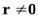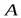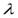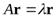Вектор , называетсясобственным вектором квадратной матрицы , если существует такое число , что . При этом число 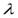называетсясобственным значением матрицы 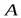, соответствующим собственному вектору 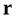. 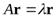может быть записано в виде 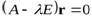.Если 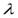- собственное значение матрицы 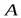, а 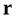соответствующий ему собственный вектор, то 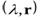называютсобственной парой матрицы .

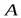Методы развёртывания векового уравнения.

1. метод Данилевского

Сущность метода заключается в приведении векового определителя к нормальному виду Фробениуса:

|p₁-λ p₂ p₃ … p_n|

|1 -λ 0 … 0|

|0 1 -λ … 0| = 0

|… … … … …|

|0 0 0 … -λ|

Метод Данилевского позволяет определить и собственные векторы с точностью до постоянного множителя.

2. метод Крылова

Характеристический полином вектора А:

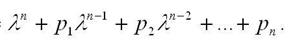= 0

Коэффициенты p_j где j=1,2,3,…n характеристического полинома определяются из системы уравнений вида:

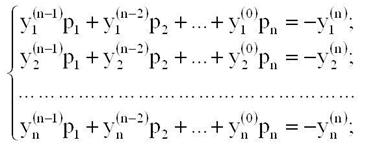
Коэффициенты вычисляются по формулам:

………

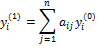
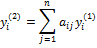
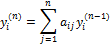
3. метод Леверрье

Основан на формулах Ньютона для сумм степеней корней алгебраического уравнения. Алгоритм метода:

1) вычисляются степени данной матрицы А

2) вычисляются суммы элементов главных диагоналей матриц

3) вычисляются коэффициенты характеристического полинома матрица А

Приближение функций. Понятие обобщённого полинома.

Данную функцию f(x) требуется заменить обобщенный полиномом Q_m(x) заданного порядка «m» так, чтобы отклонение функции f(x) от обобщенного полинома Q_m(x) на указанном множестве X={x₀, x₁,…, x_n} было наименьшим.

Обобщенный полином Q_m(x) имеет вид:

Q_m(x)=с₀*φ₀(х)+с₁*φ₁(х)+…+с_m*φ_m(x)

Интерполирование функций.

Точечное квадратичное аппроксимирование функций.

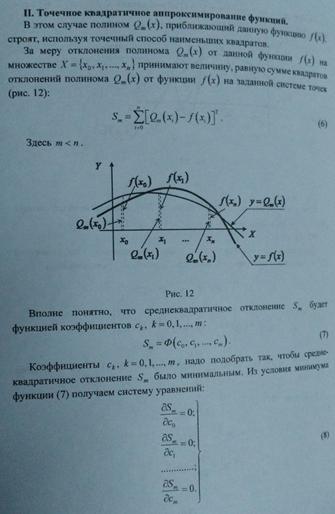
Понятие о равномерном приближении функций.

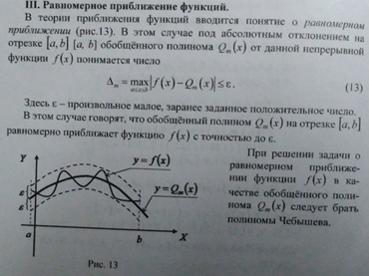
Понятие о среднеквадратичном отклонении функций на множестве параметрических точек.

Введем соответствующее расстояние 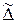между данной непрерывной функцией f(х) и непрерывным аппроксимирующим обобщенным полиномом Q(x), так называемое среднее квадратичное отклонение.Абсолютным отклонением на [а, b] обобщенного полинома Q_m (x) от данной непрерывной функции f(х) называется число

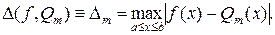
Если 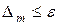, то из формулы следует 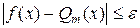для всех точек х на отрезке [а, b].

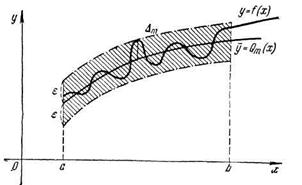
Приближённое вычисление интегралов. Формула прямоугольников.

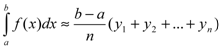приближенное значение интеграла с избытком

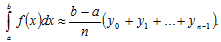приближенное значение интеграла с недостатком