Правила округления приближённых чисел.
При округлении до z значащих цифр ошибка округления  ок не должна превышать точности вычислений и максимальной ошибки округления:
ок не должна превышать точности вычислений и максимальной ошибки округления:
 ок ≤ε
ок ≤ε 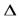 ок ≤max
ок ≤max 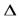 ок
ок
Правила вычисления погрешностей.
1)  А+В ≤
А+В ≤  А +
А +  В
В
2)  А+В <
А+В <  А-В
А-В
.  А+В =
А+В = 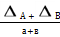
 А-В =
А-В = 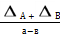
3) 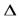 А-В ≤
А-В ≤  А +
А +  В
В
4) 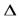 АВ ≤в*
АВ ≤в*  А +а*
А +а*  В
В  АВ ≤
АВ ≤  А+
А+  В
В
5)  А/В ≤
А/В ≤ 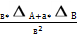
 А/В <
А/В <  А+
А+  В
В
Правила вычисления погрешностей функций и выражений.
1) метод прямых вычислений
2) метод среднего
Y=f(x);  y+=|f(x+
y+=|f(x+  x)-f(x)|;
x)-f(x)|;
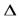 y-=|f(x-
y-=|f(x-  x)-f(x)|;
x)-f(x)|;  y=1/2(
y=1/2(  y+ +
y+ +  y-)
y-)
3) метод дифференциала
Y=f(x); dy≈Δy=|f ‘(x)|dx≈|f ‘(x)|Δx
Понятие о накоплении погрешностей при численном решении задач.
Общая погрешность: ε=εм+εок
Понятие устойчивости алгоритма вычислений.
Устойчивыми являются такие алгоритмы вычисления, для которых возникающие в процессе счета погрешности убывают или не возрастают в процессе получения решения. Для неустойчивых алгоритмов погрешности могут нарастать настолько быстро, что даже за небольшое количество шагов будет получаться совершенно неверный результат.
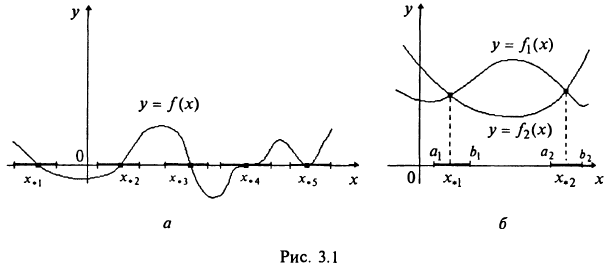
Отделение корня нелинейного уравнения, методы отделения корней.
1) средствами машинной графики: функция представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки (3.1а);
2) средствами математического анализа с помощью исследования функций и построения графиков;
3) формированием простых функций f1(x) f2(x) таких, что получается равносильное уравнение и дальнейшим построением графиков этих функций (3.1б).
Метод Крамера для решения систем линейных алгебраических уравнений.
Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.
- Для каждой переменной xi(i=1,2,…,n) необходимо составить определитель Δxi, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной систем линейных алгебраических уравнений.
3. Найти значения неизвестных по формуле xi=ΔxiΔ (i=1,2,…,n).
Метод Гаусса для решения систем линейных алгебраических уравнений.
Метод Гаусса состоит в том, что система путем эквивалентных преобразований приводят к системе с верней матрицей коэффициентов. Преобразования, допустимые в методе Гаусса:
1. Смена мест двух строк;
2. Умножение всех элементов строки на некоторое число, не равное нулю.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
4. Вычеркивание строки, все элементы которой равны нулю.
Метод простой итерации для решения систем линейных алгебраических уравнений.
Рассматривается система линейных алгебраических уравнений
Ax = b
Для применения итерационных методов система должна быть приведена к эквивалентному виду
x=Bx+d.
Затем выбирается начальное приближение к решению системы уравнений  и находится последовательность приближений к корню.
и находится последовательность приближений к корню.
Условие окончание итерации: | 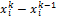 |≤ε.
|≤ε.
