Эмпирическая функция распределения и гистограмма

Эмпирической функцией распределения (функцией распределения выборки) называют функцию 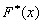, определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению 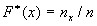, где 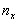– число вариант, меньших x, n – объем выборки.

В отличие от эмпирической функции распределения выборки, функцию распределения 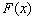генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция 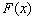определяет вероятность события X<x, тогда как эмпирическая – относительную частоту этого же события.

При росте n относительная частота события X<x, т.е. 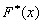стремится по вероятности к вероятности 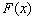этого события. Иными словами:

.

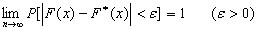Гистограмма помимо эмпирических функций распределения, наглядное (но, вместе с тем, довольно приближенное) представление о неизвестном распределении можно получить при помощи гистограмм. Для построения гистограммы относительных частот на ось абсцисс наносим интервалы

[x_k-1 , x_k] и, используя каждый из них как основание, строим прямоугольник с соответствующей высотой H_k. Получаем гистограмму.

2.Статическое оценивание и проверка гипетез. Статические методы обработки эксперементальных данных.

2.2.1 Статистические оценки параметров распределения: генеральная средняя, выборочная средняя, генеральная дисперсия, выборочная дисперсия, исправленная дисперсия.

Основные требования к точечным оценкам параметров распределения.Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности.

Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупностиЭффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной

Выборочная средняя дисперсия

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

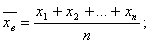
если же все значения имеют частоты n₁, n₂,…,n_k, то

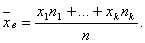
Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

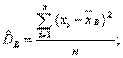
если же все значения имеют частоты n₁, n₂,…,n_k, то

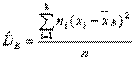
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

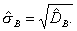
Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

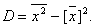
Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

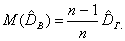
Для исправления выборочной дисперсии достаточно умножить ее на дробь

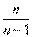
получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

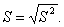
Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

2.2.2. Интервальные оценки параметров нормального распредления

Интервальной называют оценку, которая определяется двумя числами—концами интервала, покрывающего оцениваемый параметр.