Выявление согласованности мнений экспертов

После того, как цели экспертизы определены, выбран метод опроса, отобраны эксперты, начинается групповая экспертиза. И тогда возникает задача согласования оценок, полученных от экспертов.

Согласованность мнений экспертов оценивается при помощи коэффициента конкордации (согласия):

,

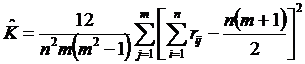где

n	- число экспертов, участвующих в опросе;
m	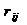- число признаков (объектов, факторов), подлежащих оценке; - ранг, приписанный i -м экспертом j-му признаку (i = 1, 2, …, n; j = 1, 2, …, m);

Чем больше 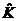, тем более согласованы мнения.

Тема 4. ИСПОЛЬЗОВАНИЕ ЭКОНОМЕТРИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ ПРИ ПРИНЯТИИ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

Эконометрические исследования, начало которым было положено в конце 20-х гг. прошлого столетия, образовали мощное самостоятельное научное направление в мировой экономической науке.

Область применения методов эконометрического моделирования и прогнозирования охватывает как макроэкономические процессы, так и уровень микроэкономики. Использование эконометрических моделей и методов, так или иначе, основано на предположении о сохранении в будущем основных причинно-следственных отношений между характеристиками исследуемого процесса и влияющими на них факторами, которые имели место на протяжении некоторого периода времени в прошлом и настоящем. Эти отношения обычно формулируются в виде уравнения, которое в самом общем случае имеют вид:

y(t) = f (x₁ (t), x₂ (t), …, x_n (t), e (t)), где (1)

y(t) – зависимая переменная, показывающая состояние исследуемого процесса в момент времени t;

x_j(t) – независимая переменная, отражающая значение j-го фактора, воздействующего на процесс y(t);

t – фактор времени;

f – функция связи между переменными модели;

e (t) – ошибка модели (отклонение фактических значений зависимой переменной от ее расчетных значений), имеющая случайный характер.

Функциональные зависимости между переменными

· Линейная функция:

y(t) = а₀ + а₁x₁ (t) + а₂x₂ (t) + …+ а_nx_n (t) + е (t), (2)

· Степенная функция:

y(t) = e ^а0 . x₁ ^а1 (t) . x₂ ^а2 (t) . … . x_n ^аn (t) . е (t), (3)

· Гиперболическая функция:

y(t) = а₀ + а₁ / x₁ (t) + а₂ / x₂ (t) + …+ а_n / x_n (t) + е (t), (4)

где а_j, j=0,1,…,n – коэффициенты (параметры) моделей, характеризующие степень влияния соответствующих факторов на зависимую переменную y;

Корреляция (лат. сorrelatio – соотношение, взаимосвязь) - это зависимость между случайными величинами.

Регрессия (лат. reqressio – движение назад) – это зависимость среднего значения какой-либо случайной величины от некоторой другой величины (парная регрессия) или нескольких величин (множественная регрессия).

Простейшим видом регрессионной модели является трендовая модель, отражающая зависимость от фактора времени. Под трендом понимается характеристика основной закономерности движения во времени.

Линейный тренд:

y(t) = а + в . t

Этапы разработки эконометрических моделей

(процесса корреляционно-регрессионного анализа)

1. Отбор факторов.

1.1. Содержательный анализ факторов, предварительный отбор.

1.2. Проверка факторов на мультиколлинеарность

Мультиколлинеарность - тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров.

На данном этапе состав предварительно отобранных факторов уточняется непосредственно по результатам статистического анализа путем построения Матрицы парных корреляций rx_ix_j..

Если коэффициент парной корреляции |rx_ix_j| близок по абсолютной величине к 1, то между двумя факторами x_i и x_j наблюдается сильная взаимосвязь и один из этих факторов должен быть исключен из дальнейшего рассмотрения.

2. Расчет параметров моделей.

На основании статистической информации, в качестве которой используются динамические ряды y(t), x_j(t), j=1,2,…,n, характеризующие известные состояния переменных в прошедшие периоды времени t=1,2,…,Т, определяется конкретный вид функциональной зависимости(1), т.е. форма модели и значения ее коэффициентов (параметров) а_j.

3. Оценка качества эконометрической модели с помощью статистических характеристик.

3.1. Коэффициент множественной корреляции R.

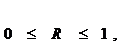
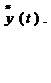R – мера тесноты связи между исходными данными y(t) и расчетными по модели данными

если R =1, то модель подобрана качественно.

3.2. Коэффициент множественной детерминации D.

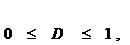D=R² – отражает изменчивость зависимой переменной y(t) от выбранных факторов.

если D =1, то модель полностью объясняет развитие исследуемого процесса в интервале t=1,2,…,Т.

D =0,88 означает, что входящие в модель факторы x_j(t) объясняют на 88% изменчивость зависимой переменной y(t) в анализируемом периоде.

3.3. Критерий Фишера (F-критерий).

F используется для оценки надежности всей модели в целом на основе определения совокупной достоверности всех ее коэффициентов.

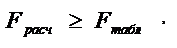Если

то можно считать, что построенная модель в целом имеет расчетные значения более близкие к истинным, чем средние значения.

3.4. Критерий Стьюдента (t).

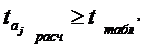С помощью критерия Стьюдента решается вопрос о значимости каждого из параметров а_j и коэффициентов x_j(t) модели.

Если

то параметр а_j значим (имеет экономическое обоснование), а фактор x_j оказывает существенное значение на зависимую переменную y(t).

Незначимые факторы удаляются из модели. Удаление производится постепенно, начиная с наименьшего значения t_aj/

Процесс построения модели можно считать завершенным, когда все факторы будут значимы и модель является надежной по всем статистическим характеристикам.

При построении удовлетворительной модели параметры а_j модели имеют экономический смысл.

Линейная модель: параметр а_j показывает, на сколько изменится зависимая переменная y(t) при изменении соответствующего фактора x_j(t) на 1.

Степенная модель: параметр а_j показывает, во сколько изменится зависимая переменная y(t) при изменении соответствующего фактора x_j(t) на 1%.

Статистические программные продукты производят оценку параметров модели с помощью метода наименьших квадратов (МНК) отклонений фактических отклонений от расчетных.

Тема 5. ИСПОЛЬЗОВАНИЕ АНАЛИТИЧЕСКИХ МОДЕЛЕЙ ВУПРАВЛЕНЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

Модели аналитического типа используются в случае, когда истиной информацией о будущем состоянии процесса является сама модель.

На основе аналитической модели исследуются, как правило, общие тенденции развития анализируемых процессов. С помощью аналитических моделей обычно даются предварительные оценки границ и пропорций развития исследуемых процессов. Обрабатывается концептуальное предположение.

Оптимизационные модели

При планировании и прогнозировании часто используются оптимизационные модели, что обусловлено наличием общих черт в прогнозных и оптимальных разработках.

1. При планировании и прогнозировании учитываются цели развития процесса. К достижению своей цели процесс, как правило, стремится оптимальным путем.

2. В прогнозных и плановых разработках есть необходимость сравнивать различные варианты путем развития процессов и выбирать из них более рациональный.

3. В прогнозах и планах необходимо учитывать ограниченность ресурсов и возможности управления.

Таким образом, в плановых и прогнозных разработках на базе оптимизационных моделей принимается во внимание принцип альтернативности, в основе которого лежит необходимость сопоставления различных вариантов развития процесса.

В целом, разработка оптимизационных моделей заключается в следующих этапах:

1. Построение формализованной модели процесса.

2. Распределение показателей модели по ее составляющим.

3. Формирование ограничений.

4. Формирование критерия эффективности развития явления.

Разработка собственного варианта развития процесса осуществляется путем решения оптимизационной задачи при тех или иных заданных значениях ограничений и выбранных вариантов критериев эффективности его развития.