Алгебра событий. Классификация событий
Операции над событиями
2.1. Записать определение. Привести свой пример. Пример: 1) Два стрелка стреляют в мишень одновременно, событие 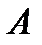 состоит в том, что в мишень попадает 1-й стрелок, а событие состоит в том, что в мишень попадает 1-й стрелок, а событие 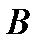 - в том, что в мишень попадает 2-й. 2) … - в том, что в мишень попадает 2-й. 2) … | ||||||||||||||||||||||||||||||||
| Операция | Определение | Смысл операции для данного примера | ||||||||||||||||||||||||||||||
Событие 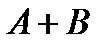 или или 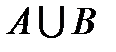
Рис.2 | 1) событие означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков. | |||||||||||||||||||||||||||||||
Событие 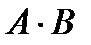 или или 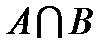
Рис.3 | 1) событие заключается в том, что в мишень попали оба стрелка. | |||||||||||||||||||||||||||||||
Событие 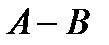 или или 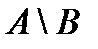
Рис.4 | 1) событие заключается в том, что первый стрелок попал в мишень, а второй промахнулся. | |||||||||||||||||||||||||||||||
Замечание. В примере 1 рассмотрены совместные события. Чему равно 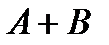 и и 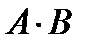 , если , если 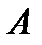 и и 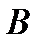 несовместные события? Дайте иллюстрацию. несовместные события? Дайте иллюстрацию. | ||||||||||||||||||||||||||||||||
2.2. Если 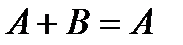 , , 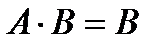 , то каковы выводы относительно событий , то каковы выводы относительно событий 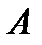 и и 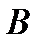 ? Дайте иллюстрацию. ? Дайте иллюстрацию. | ||||||||||||||||||||||||||||||||
2.3. Представить событие 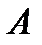 с помощью операций через с помощью операций через 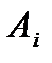 и и 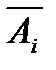 | ||||||||||||||||||||||||||||||||
1) 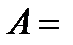 | Событие 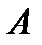 - извлечен одноцветный шар. Событие - извлечен одноцветный шар. Событие 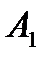 - извлечен белый шар. Событие - извлечен белый шар. Событие 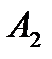 - извлечен черный шар. - извлечен черный шар. | |||||||||||||||||||||||||||||||
2) Решение. Схема в течение времени t будет работать безотказно только тогда, когда оба элемента не откажут, т.е. одновременно будут работать в течение времени t: 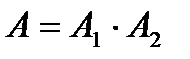 . . | 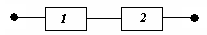 Рис.5 Релейная схема (рис.5) состоит из двух элементов. Событие Рис.5 Релейная схема (рис.5) состоит из двух элементов. Событие 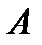 - схема в течение времени t работает безотказно. Событие - схема в течение времени t работает безотказно. Событие 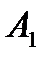 - 1-ый элемент работает безотказно в течение времени t. Событие - 1-ый элемент работает безотказно в течение времени t. Событие 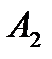 - 1-ый элемент работает безотказно в течение времени t. - 1-ый элемент работает безотказно в течение времени t. | |||||||||||||||||||||||||||||||
3) 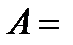 | Рис.6 Событие События | |||||||||||||||||||||||||||||||
4) а) 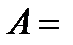 б) б) 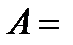 в) в) 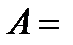 | Акционер имеет четыре акции. Пусть событие 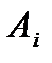 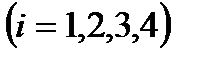 состоит в том, что состоит в том, что 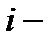 я приобретенная им акция обесценилась. Описать события я приобретенная им акция обесценилась. Описать события 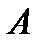 , заключающиеся в том, что: а) ни одна из акций не обесценилась; б) только одна акция упала в цене; в) не более двух акций обесценились; , заключающиеся в том, что: а) ни одна из акций не обесценилась; б) только одна акция упала в цене; в) не более двух акций обесценились; | |||||||||||||||||||||||||||||||
2.4.При проверке документа можно обнаружить четыре нарушения в его оформлении. Рассматриваются события: 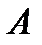 - обнаружено ровно одно нарушение; - обнаружено ровно одно нарушение; 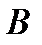 - обнаружено хотя бы одно нарушение; - обнаружено хотя бы одно нарушение; 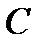 - обнаружено не менее двух нарушений; - обнаружено не менее двух нарушений; 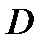 - обнаружено ровно два нарушения; - обнаружено ровно два нарушения; 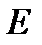 - обнаружено ровно 3 нарушения; - обнаружено ровно 3 нарушения; 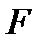 - обнаружены все нарушения. Указать в чем состоят события: а) - обнаружены все нарушения. Указать в чем состоят события: а) 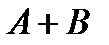 ; б) ; б) 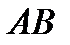 ; в) ; в) 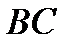 ; г) ; г) 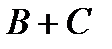 ; д) ; д) 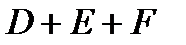 ; e) ; e) 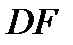 . Решение. а) . Решение. а) 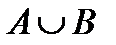 , поэтому , поэтому 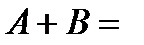 б) б) 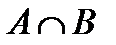 , поэтому , поэтому 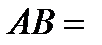 в) в) 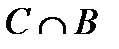 , поэтому , поэтому 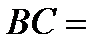 г) г) 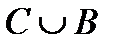 , поэтому , поэтому 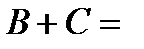 д) д) 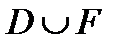 , , 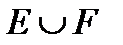 , поэтому , поэтому 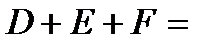 е) е) 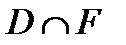 , поэтому , поэтому 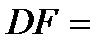 | ||||||||||||||||||||||||||||||||
2.5. Среди студентов, собравшихся на лекцию по теории вероятностей, выбирают наудачу одного. Пусть событие 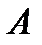 заключается в том, что он — юноша. Событие заключается в том, что он — юноша. Событие 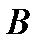 в том, что он не курит, а событие в том, что он не курит, а событие 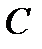 в том, что он живет в общежитии. а) Описать событие в том, что он живет в общежитии. а) Описать событие 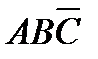 . б) При каком условии будет иметь место тождество . б) При каком условии будет иметь место тождество 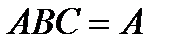 ? в) Когда будет справедливо соотношение ? в) Когда будет справедливо соотношение 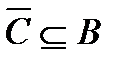 ? г) Когда будет верно равенство ? г) Когда будет верно равенство 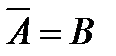 , будет ли оно иметь место, если все юноши курят? Решение. , будет ли оно иметь место, если все юноши курят? Решение. | ||||||||||||||||||||||||||||||||
2.6. Имеется 4 изделия, каждое из которых может быть либо бракованным, либо хорошим. Введем события: 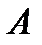 - хотя бы одно изделие бракованное; - хотя бы одно изделие бракованное; 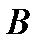 - бракованных не менее двух изделий. Описать события: - бракованных не менее двух изделий. Описать события: 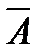 , , 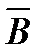 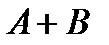 , , 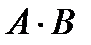 , , 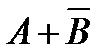 , , 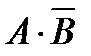 , , 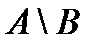 . Решение. . Решение. | ||||||||||||||||||||||||||||||||
Определение вероятности
Основные теоремы
Решение.
Повторение испытаний
| 5.1. Заполнить пропуски и записать соответствующие формулы. |
Формула Бернулли. Вероятность того, что в 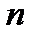 независимых испытаниях, в каждом из которых вероятность появления события равна независимых испытаниях, в каждом из которых вероятность появления события равна 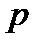 , событие наступит ровно , событие наступит ровно 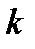 раз (безразлично, в какой последовательности), равна: раз (безразлично, в какой последовательности), равна: 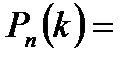 Вероятность того, что в Вероятность того, что в 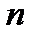 независимых испытаниях, в каждом из которых вероятность появления события равна независимых испытаниях, в каждом из которых вероятность появления события равна 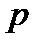 , событие наступит не менее , событие наступит не менее 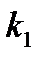 и не более и не более 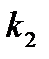 раз, равна: раз, равна: 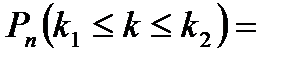 Вероятность того, что в Вероятность того, что в 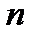 независимых испытаниях, в каждом из которых вероятность появления события равна независимых испытаниях, в каждом из которых вероятность появления события равна 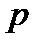 , событие наступит хотя бы один раз, равна: , событие наступит хотя бы один раз, равна: 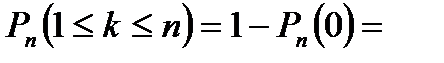 |
Теорема Пуассона. Если существует 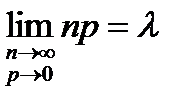 , то справедливо приближение Пуассона , то справедливо приближение Пуассона 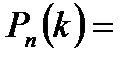 где где 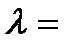 Практическое использование формулы допустимо при Практическое использование формулы допустимо при 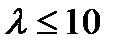 , , 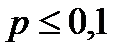 . . |
Локальная теорема Лапласа. Вероятность того, что в 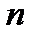 независимых испытаниях, в каждом из которых вероятность появления события равна независимых испытаниях, в каждом из которых вероятность появления события равна
|

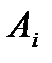 -
- 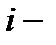 ый блок пропускают ток.
ый блок пропускают ток.