Сравнение двух математических ожиданий.
Пусть имеются две выборки х1, х2,..., xn и y1, y2,..., ym, полученные в результате независимых испытаний. По этим данным рассчитаны оценки 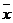 и
и 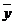 , а так же
, а так же 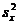 и
и 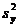 . В предположении, что случайные величины X и Y распределены по нормальному закону
. В предположении, что случайные величины X и Y распределены по нормальному закону 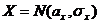 и
и 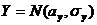 , требуется проверить на основании выборочных данных гипотезу
, требуется проверить на основании выборочных данных гипотезу 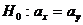 при условии, что гипотеза о равенстве дисперсий не отвергается.
при условии, что гипотеза о равенстве дисперсий не отвергается.
Задача 3. Средний ежедневный объем продаж за I квартал текущего года для 17 торговцев района А составляет 15 тыс. руб. при «исправленном» среднем квадратичном отклонении 2,5 тыс. руб., а для 10 торговцев района В – 13 тыс. руб. при «исправленном» среднем квадратичном отклонении 3 тыс. руб. Каждую группу можно считать случайной независимой выборкой из большой совокупности. Существенно ли различие объемов продаж в районах А и В при 5%-м уровне значимости?
Решение. Предположим, что ежедневный объем продаж подчинен нормальному закону распределения. Математическое ожидание и среднее квадратичное отклонение законов распределения для районов А и В неизвестны. Предположим, что дисперсии объемов продаж одинаковы. В этих условиях возникает задача оценки статистической гипотезы 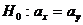 при альтернативной
при альтернативной 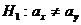 , если принять за ax математическое ожидание объема продаж для района А, за ay – для района В.
, если принять за ax математическое ожидание объема продаж для района А, за ay – для района В.
Выборочные средние 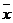 и
и 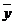 являются независимыми нормально распределенными случайными величинами. В этом случае в качестве критерия используют функцию
являются независимыми нормально распределенными случайными величинами. В этом случае в качестве критерия используют функцию
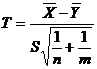 , где
, где 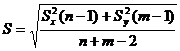 .
.
Функция Т подчинена t-распределению для 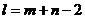 степеней свободы.
степеней свободы.
По таблице t-распределения для 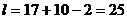 и 5%-го уровня значимости (для двусторонней критической области) находим tкр=2,06. Это значит, что критическая область есть интервал
и 5%-го уровня значимости (для двусторонней критической области) находим tкр=2,06. Это значит, что критическая область есть интервал 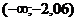 и
и 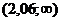 .
.
Вычислим tr:
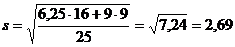 ,
,
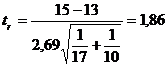 .
.
Полученное значение критерия tr не принадлежит критической области, следовательно, разность несущественна и гипотеза 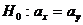 принимается. В качестве общей средней выборочной принимают величину
принимается. В качестве общей средней выборочной принимают величину
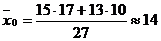 .
.
Задача 4. В условиях задачи 3 выяснить, существенно ли при 5%-ном уровне значимости превышение обхема продаж в районе А по сравнению с объемом в районе В.
Решение. Вопрос в данной задаче отличается от вопроса в задаче 3 тем, что альтернативной к гипотезе 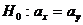 становится не гипотеза
становится не гипотеза 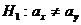 , а гипотеза
, а гипотеза 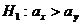 . В этом случае критическая область односторонняя (в частности, правосторонняя), для l=25 и α=0,05 имеем критическую область
. В этом случае критическая область односторонняя (в частности, правосторонняя), для l=25 и α=0,05 имеем критическую область 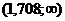 . Так как tr=1,86>1,708, то величина tr входит в критическую область, поэтому превышение объема продаж в районе А по сравнению с объемом в районе В существенно и гипотеза
. Так как tr=1,86>1,708, то величина tr входит в критическую область, поэтому превышение объема продаж в районе А по сравнению с объемом в районе В существенно и гипотеза 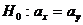 отвергается.
отвергается.
Задача 5. Фирма предлагает автоматы по розливу напитков. При выборке n=16 найдена средняя величина 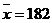 г дозы, наливаемой в стакан автоматом №1. По выборке m=9 найдена средняя величина
г дозы, наливаемой в стакан автоматом №1. По выборке m=9 найдена средняя величина 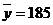 г дозы, наливаемой в стакан автоматом №2. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсией, равной
г дозы, наливаемой в стакан автоматом №2. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсией, равной 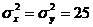 г2. Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости α=0,01?
г2. Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости α=0,01?
Решение. Пусть ax и ay – математические ожидания доз, наливаемых автоматом №1 и автоматом №2. Нулевая гипотеза в данном случае 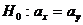 при альтернативных
при альтернативных 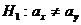 и
и 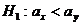 . Дисперсия известна: σ2=25. В качестве критерия справедливости статистической гипотезы выбирается функция
. Дисперсия известна: σ2=25. В качестве критерия справедливости статистической гипотезы выбирается функция
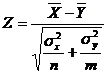 ,
,
рапределенная по нормальному закону с параметрами (0, 1).
1. Рассмотрим вначале гипотезу 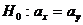 для альткрнативной
для альткрнативной 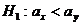 . В этом случае критическая область имеет вид
. В этом случае критическая область имеет вид 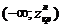 , где
, где 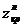 определяется из условия
определяется из условия 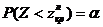 .
.
Так как функция Лапласа – нечетная функция, т.е. 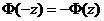 , а таблица этой функции содержит только положительные значения, то найдем вначале
, а таблица этой функции содержит только положительные значения, то найдем вначале 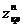 .
.
Для этого вычислим значение функции Лапласа в критической точке: 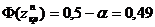 . Откуда
. Откуда 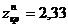 . Значит, левосторонняя критическая область будет
. Значит, левосторонняя критическая область будет 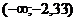 .
.
Рассчитаем zr:
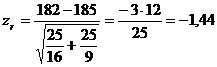 .
.
Полученное значение zr= –1,44 не входит в критическую область 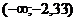 , поэтому нулевая гипотеза принимается.
, поэтому нулевая гипотеза принимается.
2. Рассмотрим гипотезу 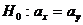 при альтернативной
при альтернативной 
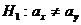 . В этом случае критическая область двусторонняя и имеет вид
. В этом случае критическая область двусторонняя и имеет вид 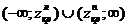 . Величины
. Величины 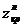 и
и 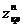 рассчитываются из условий
рассчитываются из условий
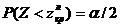 и
и 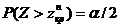 .
.
Воспользовавшись таблицей функции Лапласа, имеем
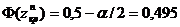 ,
,
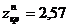 .
.
Критическая область имеет вид 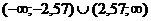 . Значение zr= –1,44 не попадает в критическую область, поэтому нулевая гипотеза принимается.
. Значение zr= –1,44 не попадает в критическую область, поэтому нулевая гипотеза принимается.
