Основные распределения и их числовые характеристики.
1) Биноминальное:


2) Пуассона:


3) Равномерное:



4) Нормальное:
Вероятность попадания случайной величины в интервал (a, b) находится по формуле

где  - функция Лапласа.
- функция Лапласа.

5) Логнормальное:


6) Хи-квадрат:


7) Стьюдента:


8) Фишера-Снедекора:


Цель занятий: 1. Добиться усвоения свойств функции распределения и функции плотности вероятности.
2. Изучение некоторых стандартных распределений (показательного, нормального и т.д.). При этом полезно назвать возможные приложения этих законов распределения.
3. Выработать навыки вычисления числовых характеристик случайных величин и вероятности попадания в интервал.
4.Желательно научить студентов считывать информацию о случайной величине с графика функции распределения и функции плотности вероятности. Рекомендуется случайные величины обозначить большими буквами X,Y,Z и т. д., а возможные значения - соответственно малыми буквами x, y, z и т.д.
Студенты должны быть готовы ответить на следующие вопросы:
1. Каким образом могут быть заданы дискретные, непрерывные и смешанные случайные величины?
2. Что является полной статистической характеристикой случайной величины?
3. Какие размерности имеют функция распределения и плотность вероятности?
4. Каким образом функция распределения связана с вероятностью?
5. Может ли при каком-либо значении аргумента быть
– функция распределения больше единицы?
– плотность распределения больше единицы?
–функция распределения отрицательной?
– плотность распределения отрицательной?
6. С какой целью вводятся числовые характеристики случайных величин?
7.Какова размерность математического ожидания, дисперсии, среднего квадратического отклонения, третьего, четвертого начальных и центральных моментов?
Задача 1. Монета подбрасывается 5 раз. Написать закон распределения случайной величины, равной числу выпавших гербов минус число выпавших цифр. Построить многоугольник распределения, функцию распределения.
Решение. Случайная величина X – число выпавших гербов минус число выпавших цифр – имеет следующие возможные значения:
х 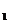 = -5, х
= -5, х 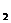 = -3, х
= -3, х 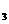 = -1, х
= -1, х 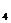 =1, х
=1, х  =3, х
=3, х  =5.
=5.
Подбрасывания монеты можно рассматривать как независимые испытания, вероятность выпадения герба в каждом из которых равна р =  . Поэтому применима формула Бернулли:
. Поэтому применима формула Бернулли:
Р(Х=5)=Р(Х= -5)=Р  (0)=С
(0)=С 

 =
=  ,
,
Р(Х=3)=Р(Х= -3)=Р  (1)= С
(1)= С 

 =
=  ,
,
Р(Х=1)=Р(Х= -1)=Р  (2)= С
(2)= С 

 =
=  .
.
Напишем закон распределения:
| X | -5 | -3 | -1 | |||
| P | 1/32 | 5/32 | 10/32 | 10/32 | 5/32 | 1/32 |
 Построим многоугольник распределения (рис. 2).
Построим многоугольник распределения (рис. 2).
Рис. 2.
Построим функцию распределения (рис. 3)

 |
Рис. 3.
Задача 2. Некто имеет на связке 5 ключей. При отмыкании замка последовательно один за другим испытывает ключи, пока не подберет нужный ключ. Написать закон распределения числа испытанных ключей. Подсчитать математическое ожидание этой случайной величины. Построить многоугольник распределения и функцию распределения.
Решение. Возможные значения числа попыток 1, 2, 3, 4, 5. Найдем вероятности этих значений. Случайная величина Х примет значение х 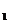 =1, если мы попадем с первой попытки, вероятность чего р
=1, если мы попадем с первой попытки, вероятность чего р 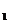 =
=  . Случайная величина Х примет значение х
. Случайная величина Х примет значение х  = 2, если при первой попытке мы не попадем (вероятность чего
= 2, если при первой попытке мы не попадем (вероятность чего  ) и попадем при второй попытке (вероятность чего
) и попадем при второй попытке (вероятность чего 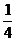 , в силу зависимости событий), т. е. Р( Х=2)=
, в силу зависимости событий), т. е. Р( Х=2)=  ×
× 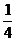 =
=  ;
;
Аналогично: Р( Х=3)=  ×
× 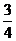 ×
×  =
=  ,
,
Р(Х = 4) =  ×
× 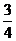 ×
×  ×
×  =
=  , P (Х =5) =
, P (Х =5) =  ×
× 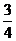 ×
×  ×
×  ×1=
×1=  .
.
В итоге:
| X | 1 | 2 | 3 | 4 | 5 |
| P | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
М (Х) = 1×  + 2×
+ 2×  + 3×
+ 3×  + 4×
+ 4×  + 5×
+ 5×  =3.
=3.
Рекомендуется построить многоугольник распределения и функцию распределений по аналогии с 1-й задачей.
Задача 3. Вероятность попадания в цель при одном выстреле равна р. Написать закон распределения числа выстрелов до первого попадания в цель. Подсчитать математическое ожидание этой случайной величины.
Решение. Величина Х примет значения  , если будет попадание при первом же выстреле, вероятность чего равна p. Понадобится два выстрела (величина Х примет значение х
, если будет попадание при первом же выстреле, вероятность чего равна p. Понадобится два выстрела (величина Х примет значение х 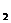 =2), если при первом выстреле не попадем (вероятность чего q=1-p) и при втором попадем с вероятностью р (в силу независимости испытаний), т.е. Р(Х=2)= q× р.
=2), если при первом выстреле не попадем (вероятность чего q=1-p) и при втором попадем с вероятностью р (в силу независимости испытаний), т.е. Р(Х=2)= q× р.
Аналогично
 Р( Х=3) = q × q × р = q
Р( Х=3) = q × q × р = q 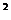 × р,…, Р(Х=
× р,…, Р(Х= 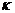 ) = q × q× …. ×q × р = qk–1×р.
) = q × q× …. ×q × р = qk–1×р.
k–1 раз
В результате закон распределения случайной величины имеет вид
| X | 1 | 2 | 3 | … | k | … |
| P | p | Qp | q 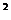 p p | … | q  p p | … |
Это геометрический закон распределения.

(получаем сходящийся ряд, так как  ).
).
Задача 4. В партии из 10 деталей содержится три нестандартных. Наудачу отобрали две детали. Написать закон распределения числа нестандартных деталей среди двух отобранных. Подсчитать математическое ожидание этой случайной величины.
Решение. Случайная величина X – число нестандартных деталей среди двух отобранных имеет следующие возможные значения: 

 Найдем их вероятности
Найдем их вероятности



Составим искомый закон распределения случайной величины
| X | 0 | 1 | 2 |
| P | 7/15 | 7/15 | 1/15 |
Находим математическое ожидание
 .
.
Задача 5.Вероятный прогноз для величины Х – процентного изменения стоимости акций по отношению к их текущему курсу в течении шести месяцев – дан в виде закона распределения:
| X | ||||||
| P | 0,1 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 |
Найти вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 36% годовых.
Решение. Прирост суммы на банковском депозите при условии 3% в месяц составит через 6 месяцев  Вероятность того, что покупка акций выгоднее банковского депозита, определяется суммой вероятностей, соответствующих более высокому росту курса акций:
Вероятность того, что покупка акций выгоднее банковского депозита, определяется суммой вероятностей, соответствующих более высокому росту курса акций:

Задача 6. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в некотором автосалоне составляют в среднем 100 тыс. р., а число продаж Х автомашин в течение дня подчиняется следующему закону распределения:
| Х | ||||||||||
| Р | 0,25 | 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 | 0,025 | 0,025 |
а)Найти математическое ожидание ежедневной прибыли при цене на машину 150 тыс. р.. б) Дисперсию ежедневной продажи числа автомашин.
Решение. а)Ежедневная прибыль подсчитывается по формуле
П = (150Х – 100)тыс. р.
Искомая характеристика М(П) находится с использованием указанных выше свойств математического ожидания (в тыс. р.):
М(П)=М(150Х–100)=50М(Х)–100=150∙2,675–100 = 301,25.
б) Закон распределения случайной величины Х2 имеет вид:
| Х2 | ||||||||||
| Р | 0,25 | 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | 0,05 | 0,05 | 0,025 | 0,025 |
Математическое ожидание М(Х2) подсчитывается из этой таблицы:
М(Х2) = 0 ∙ 0,25 + 1 ∙ 0,2 + 9 ∙ 0,1 + 16 ∙ 0,1 + 25 ∙ 0,1 + 36 ∙ ∙0,05 + 49 ∙ 0,05 + 64 ∙ 0,025 + 81 ∙ 0,025 = 13,475.
Математическое ожидание М(Х) = 2,675. Следовательно, получаем искомую величину дисперсии:

Задача 7. Случайная величина X задана на всей оси функцией распределения  . Найти функцию плотности вероятности и вероятность того, что X примет значение, заключенное в интервале (0,1).
. Найти функцию плотности вероятности и вероятность того, что X примет значение, заключенное в интервале (0,1).
Решение. По определению 

Полезно сопроводить решение задачи рис.4.

 Задача 8. Функции распределения случайной величины имеет вид, изображенный на рис.5.
Задача 8. Функции распределения случайной величины имеет вид, изображенный на рис.5.

Найти: a)функцию плотности вероятности; б) глядя на график F(x), указать основные особенности случайной величины, например, интервал возможных значений, наиболее вероятные значения и т.д.; в) M(X), D(X); г) P(X<1), P(1<X<2).
Решение. a) 
б)  ,
,  ;
;
в)  ,
,
 .
.
Задача 9. Функция распределения времени имеет вид 
 где
где  - некоторый параметр. Найти функцию плотности вероятности. Найти математическое ожидание этой случайной величины. Если
- некоторый параметр. Найти функцию плотности вероятности. Найти математическое ожидание этой случайной величины. Если  то вычислить вероятность
то вычислить вероятность 
Решение. По определению 



Задача 10. Поезда метро следуют с интервалом 2 минуты. Пассажир в случайный момент времени приходит на платформу. Указать функцию распределения времени ожидания пассажира. Найти и построить функцию плотности вероятности времени ожидания. Найти математическое ожидание и дисперсию времени ожидания.
Решение. Естественно предположить, что равновозможно прибытие пассажира в любой момент времени между прибытиями поездов. Формально это означает, что время ожидания X имеет равномерный закон распределения, с плотностью вероятности

Тогда  см. рис. 6.
см. рис. 6.



Задача 11. Систематическая ошибка высотометра равна+20 м, а случайная ошибка распределена по нормальному закону со средним квадратичным отклонением 60 м. Какова вероятность того, что ошибка измерения не превысит по абсолютной величине 100 м?
Решение. Случайная величина  .
.

Из рис. 7 видно, что нужно вычислить вероятность равную заштрихованной площади, т. е.

Задача 12.Магазин производит продажу мужских костюмов. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равными 48 и 2. Определить процент спроса на 50-й размер при условии разброса значений этой величины в интервале (49, 51).
Решение. По условию задачи 
Вероятность спроса на 50-й размер в заданном интервале равна

Следовательно, спрос на 50-й размер костюмов составит около 24%, и магазину нужно предусмотреть это в общем объёме закупки.
Задача 13. Для годной детали допустимо отклонение от номинала не более чем два микрона. Случайное отклонение размера детали от номинала при изготовлении её на данном станке имеет нулевое математическое ожидание и среднее квадратическое отклонение 5мк. Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная? 
Решение. Отклонение от номинала X имеет закон распределения N(0,52). Тогда вероятность того, что деталь годная, равна

Изготовление детали рассматриваем как независимый опыт с вероятностью “успеха” p=0,31. Тогда необходимое число деталей определяется из соотношения

Дополнительные задачи.
Задача 1.В лотерее разыгрывается: автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью 250 ден. ед., 5 видеомагнитофонов стоимостью 200 ден. ед. Всего продаётся 1000 билетов по 7 ден. ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет.
Решение. Возможные значения случайной величины Х – чистого выигрыша на один билет – равны 0 – 7 = -7 ден. ед. (если билет не выиграл), 200 – 7 =193, 250 – 7 =243, 5000 – 7 = =4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и 1, и используя классическое определение вероятности, получим:


т.е. ряд распределения
| Х | -7 | |||
| Р | 0,990 | 0,005 | 0,004 | 0,001 |
Задача 2.Вероятность того, что студент сдаст семестровый экзамен в сессию по дисциплинам А и Б, равны соответственно 0,7 и 0,9. Составить закон распределения числа семестровых экзаменов, которые сдаст студент.
Решение. Возможные значения случайной величины Х - числа сданных экзаменов – 0, 1, 2.
Пусть Ai – событие, состоящее в том, что студент сдаст i-й экзамен (i=1,2). Тогда вероятность того, что студент сдаст в сессию 0,1,2 экзамена, будут соответственно равны (считаем события А1и А2 независимыми):



Итак ряд распределения случайной величины
| Х | |||
| Р | 0,03 | 0,34 | 0,63 |
Задача 3.Вычислить М(Х) для случайной величины Х - чистого выигрыша по данным задачи 1.
Решение.
 т.е. средний выигрыш равен нулю. Полученный результат означает, что вся выручка от продажи билетов идёт на выигрыши.
т.е. средний выигрыш равен нулю. Полученный результат означает, что вся выручка от продажи билетов идёт на выигрыши.
Задача 4. Известны законы распределения случайных величин X и Y – числа очков, выбиваемых 1-м и 2-м стрелками.
| X | |||||||||||
| P | 0,15 | 0,11 | 0,04 | 0,05 | 0,04 | 0,1 | 0,1 | 0,04 | 0,05 | 0,12 | 0,2 |
| Y | |||||||||||
| P | 0,01 | 0,03 | 0,05 | 0,09 | 0,11 | 0,24 | 0,21 | 0,1 | 0,1 | 0,04 | 0,02 |
Необходимо выяснить, какой из двух стрелков стреляет лучше.
Рассматривая ряды распределения случайных величин X и Y, ответить на этот вопрос далеко не просто из-за обилия числовых значений, К тому же у первого стрелка достаточно большие вероятности (например, больше 0,1) имеют крайние значения числа выбиваемых очков (X = 0; 1 и X = 9; 10), а у второго стрелка – промежуточные значения (Y = 4; 5; 6).
Очевидно, что из двух стрелков лучше стреляет тот, кто в среднем выбивает большее количество очков.
Вычислим M(X) и M(Y)

 т.е среднее число выбиваемых очков у двух стрелков одинаковое.
т.е среднее число выбиваемых очков у двух стрелков одинаковое.
Задача 5.В задаче 4 вычислить дисперсию и среднее квадратическое отклонение числа выбитых очков для каждого стрелка.




Итак, при равенстве средних значений числа выбиваемых очков (M(X)=M(Y)) его дисперсия, т.е. характеристика рассеяния относительно среднего значения, меньше у второго стрелка (D(X)<D(Y)) и, очевидно, ему для получения более высоких результатов стрельбы по сравнению с первым стрелком нужно сместить «центр» распределения числа выбиваемых очков, т.е. увеличить M(Y), научившись лучше целиться в мишень.
Задача 6.По многолетним статистическим данным известно, что вероятность рождения мальчика равна 0,515. Составить закон распределения случайной величины Х – числа мальчиков в семье из 4 детей. Найти математическое ожидание и дисперсию этой случайной величины.
Решение.Число мальчиков в семье из n = 4 представляет случайную величину Х с множеством значений Х = m =0, 1, 2, 3, 4, вероятности которых определяются по формуле Бернулли:
 где q = 1 – p.
где q = 1 – p.
В нашем случае n = 4, p = 0,515, q = 1 – p = 0,485.
Вычислим





Ряд распределения имеет вид
| Х | |||||
| Р | 0,055 | 0,235 | 0,375 | 0,265 | 0,070 |
Убеждаемся, что 
Учитывая, что закон распределения случайной величины X биномиальный имеем


Задача 7. Ряд распределения дискретной случайной величины состоит из двух неизвестных значений. Вероятность того, что случайная величина примет одно из этих значений равна 0,8. Найти функцию распределения случайной величины, если её математическое ожидание равно 3,2, а дисперсия 0,16.
Решение.Ряд распределения имеет вид
| Х | Х1 | Х2 |
| Р | 0,8 | 0,2 |
где pi = 0,8, а p2 = 1 – p1 = 1 – 0,8 = 0,2.
По условию

или 
Решая полученную систему, находим два решения:
 и
и 
Записываем выражение функции распределения:

или 
Задача 8.Дана функция распределения случайной величины X:

а) Найти плотность вероятности f(x); б) построить графики f(x) и F(x); в) убедиться в том, что X – непрерывеая случайная величина; г) найти вероятности P(X=1), P(X<1), P(1≤X<2) (две последние вероятности показать на графиках f(x) и F(x)); д) вычислить математическое ожидание M(X), дисперсию D(X), моду Мо(Х), и медиану Ме(Х).
Решение. а) Плотность вероятности

б) Графики f(x) и F(x) изображены на рис. 8 а и б.
в) Случайная величина Х – непрерывная, так как функция распределения F(x) непрерывна, а её производная – плотность вероятности f(x) – непрерывна во всех точках, кроме одной (x = = 2);
г) P(X=1) = 0 как вероятность отдельно взятого значения непрерывной случайной величины.
P(X<1) можно найти либо по определению функции распределения, либо по формуле через плотность вероятности f(x):
 (ордината графика F(1) – см. рис. 8б – или
(ордината графика F(1) – см. рис. 8б – или

(площадь под кривой распределения f(x) на отрезке [0;1] – см. рис. 8а).
P(1≤X≤2) можно найти либо как приращение функции распределения, либо через плотность вероятности f(x):

(приращение ординаты графика F(X) на отрезке [1;2] – рис. 8б) – или 
(площадь под кривой распределения f(x) на отрезке [1;2] – рис. 8а).
д)



Плотность вероятности f(x) максимальна при x=2, следовательно, Мо(Х)=2.
Медиану Ме(X)=b найдём из условия  т.е.
т.е.  откуда
откуда  или через плотность вероятности
или через плотность вероятности
 т.е.
т.е. 
откуда 
Задача 9. Банк выдаёт 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждого из заёмщиков. Составить таблицу закона распределения количества заёмщиков, не вернувших кредит по окончанию срока кредитования. Найти математическое ожидание числа невозврата кредитов.
Решение.Примем за А событие невозврата кредита. Так как заёмщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невозврата k кредитов из 5 описывается биномиальным распределением, где p = 0,2, q = 0,8, m принимает значения от нуля до 5. Таблица закона распределения имеет вид:
| X | |||
| P | (0,2)5 | 5(0,2)4(0,8) | 10(0,2)3(0,8)2 |
| X | |||
| P | 10(0,2)2(0,8)3 | 5(0,2)(0,8)4 | (0,8)5, |
или окончательно:
| X | ||||||
| P | 0,00032 | 0,0064 | 0,0512 | 0,2048 | 0,4096 | 0,32768. |

Задача 10. Банк выдал ссуды n разным заёмщикам в размере S р. каждому под ставку ссудного процента r. Найти а) математическое ожидание и дисперсию прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата ссуды заёмщиком равна p; б) математическое ожидание и среднее квадратическое отклонение прибыли при n =1000, p =0,8, S = 100 тыс. р. и r = 30%.
Решение. а) Поскольку заёмщики между собой не связаны, то можно полагать, что мы имеем n независимых испытаний. Вероятность утери ссуды для банка в каждом испытании равна q = = 1 – p. Пусть X – число заёмщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формулой
П = (1+r/100)SX – nS,
где X является случайной величиной с биномиальным законом распределения.
М(П) = (1 + r/100)SM(X) – nS =
= (1 + r/100)Snp – Sn = Sn(rp/100 – q).
Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная средняя величина прибыли), то из условия М(П) > 0 вытекает условие на ставку ссудного процента:
r > 100q/p, или r > 100(1 – p)/p.
D(П) = D((1 + r/100)SX – nS) = (1 + r/100)2S2npq.
б) Ставка ссудного процента удовлетворяет условию, чтобы математическое ожидание прибыли было положительным: 30 >100(1 – 0,8)/0,8. Математическое ожидание прибыли:
М(П) = Sn(rp/100 – q) =
= 100 ∙ 1000(30 ∙ 0,8/100 – 0,2) = 4 млн. р.
Среднее квадратическое отклонение прибыли:

Домашнее задание.
Задача 1. В партии из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон распределения числа дефектных курток среди купленных. Построить многоугольник распределения.
Задача 2. Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3. Аудитору на заключение представлено 3 баланса предприятия. Составить закон распределения числа положительных заключений на проверяемые балансы.
Задача 3. Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель равна 0,8, а вероятность того, что второй – 0,6. Случайная величина Х – число покупок, сделанных покупателями. Описать закон распределения случайной величины Х.
Задача 4. Два консервных завода поставляют продукцию в магазин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90%, а на втором – 80%. В магазине куплено 3 банки консервов. Найти математическое ожидание и среднее квадратическое отклонение числа банок с продукцией высшего качества.
Задача 5. Плотность вероятности непрерывной случайной величины Х задана в интервале (–π/2; π/2) функцией  Вне этого интервала
Вне этого интервала  Найти параметр С и определить вероятность попадания случайной величины Х в интервал (0; π/4).
Найти параметр С и определить вероятность попадания случайной величины Х в интервал (0; π/4).
Задача 6. Случайная величина Х задана плотностью вероятности  при – ∞ < x < ∞. Определить параметр
при – ∞ < x < ∞. Определить параметр  и математическое ожидание.
и математическое ожидание.
Задача 7.Паром для перевозки автомашин через залив подходит к причалу через каждые два часа. Считая, что время прибытия автомашин – случайная величина Х – распределено равномерно, определить среднее время ожидания автомашиной прихода парома и дисперсию времени ожидания.
Задача 8. Математическое ожидание нормально распределённой случайной величины – количества сыра, используемого для изготовления 100 бутербродов, – равно 1 кг. Известно, что с вероятностью 0,96 расход сыра на изготовление 100 бутербродов составляет от 900 до 1100г. Определить среднее квадратичное отклонение расхода сыра на 100 бутербродов.
Ответы:
| X | ||||
| P | 114/230 | 95/230 | 20/230 | 1/230, |
1)
| X | ||||
| P | 0,027 | 0,189 | 0,441 | 0,343, |
2)
| X | |||
| P | 0,48 | 0,44 | 0,08, |
3)
4)M(X) = 2,519, σ(X) ≈ 0,64; 5)C = 1/2; 6)  7)Mx = =1ч., Dx = 1/3 ч2; 8)σx = 48,8 г.
7)Mx = =1ч., Dx = 1/3 ч2; 8)σx = 48,8 г.
СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Г. С. ЕВДОКИМОВА
ПРАКТИКУМ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
МОДУЛЬ 6
Предельные теоремы теории вероятностей.
Смоленск 2009
Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:
P(|X-a|> ε)≤  (1)
(1)
или
P(|X-a|≤ ε)≥ 1- 
где a=M(X), ε >0.
Теорема Чебышева: Если дисперсии n независимых случайных величин X1, X2 ,... Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайная величина сходится по вероятности к средней арифметической их математических ожиданий, т.е.

Следствие: Если независимые случайные величины X1,X2,...,Xn имеют одинаковые математические ожидания, равные a, а их дисперсии ограничены одной и той же постоянной, то неравенство Чебышева и теорема Чебышева примут вид:


Теорема Бернулли: Относительная частота событий в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности p этого события в отдельном испытании:

Центральная предельная теорема для одинаково распределенных величин: Если X1,X2 ,...,Xn – независимые случайные величины, у которых существуют равные математические ожидания M[Xi]=a, дисперсии D[Xi]=a2 и абсолютные центральные моменты третьего порядка M(|Xi-ai|3)=mi, (  ), то закон распределения суммы Yn=X1+X2+...+Xn при
), то закон распределения суммы Yn=X1+X2+...+Xn при 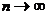 неограниченно приближается к нормальному. В частности, если все случайные величины Xi одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при
неограниченно приближается к нормальному. В частности, если все случайные величины Xi одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при 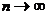 .
.
Локальная теорема Муавра-Лапласа: Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность Pm,n того, что событие A произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна
 ,
,
где

и
 .
.
Pmin=Pn(m).
Интегральная теорема Муавра-Лапласа: Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события A в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n приближенно равна
 ,
,
где
 –
–
функция (или интеграл вероятностей) Лапласа;
 ,
,  .
.
Цель занятия: 1. Добиться усвоения условий применения центральной предельной теоремы.
2. Закрепить навыки вычисления вероятностей, связанных с нормальным законом распределения.
3. Научит
