Формула бернулли и ее асимптотические приближения

Если вероятность наступления события A в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события A. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления событияAв каждом испытании одна и та же. Описанная последовательность независимых испытаний называется схемой Бернулли.

Пусть производится nнезависимых опытов, в каждом из которых с одной и той же вероятностью pможет наступить некоторое событие A. Требуется для заданного числа kнайти вероятность следующего события: в nопытах событие A наступит ровно k раз.

Чтобы подчеркнуть зависимость полученного выражения от nи k, обозначим его через 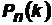. Вероятность появления события Aв nнезависимых испытаниях ровно k раз равна:

.

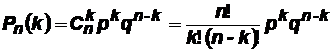Полученная формула называется формулой Бернулли.

В ряде случаев требуется определить вероятности появления событияА менее kраз (X<k), более kраз (X>k), не менее kраз (X≥k), не более kраз (X≤k). В этих случаях могут быть использованы формулы:

,

,

,

.

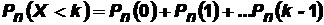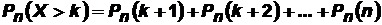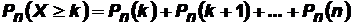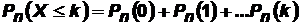Наивероятнейшее число появлений события в n независимых испытаниях определяют по формуле:

.

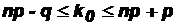Количество n опытов, которые нужно произвести для того, чтобы с вероятностью не меньше P можно было утверждать, что данное событие произойдёт по крайней мере один раз, находится по формуле:

,

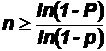где p– вероятность появления этого события в каждом опыте.

Теорема.Если вероятность события p наступления события Ав каждом испытании очень мала: 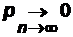при неограниченном увеличении числа испытаний (такие события называются редкими), причем произведение npстремится к постоянному числу λ, то вероятность 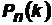того, что событие А появится k раз в nнезависимых испытаниях, удовлетворяет предельному равенству:

.

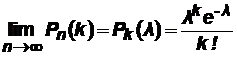Эта формула называется формулой Пуассона (должны выполняться следующие условия: ; ; ).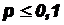

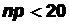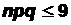Значения функции Пуассона 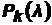приведены в Приложении №3.Приведём значения функции Пуассона для небольших значений λ:

λ k	0,1	0,2	0,3	0,4	0,6	0,7	0,8	0,9
	0,904	0,818	0,740	0,670	0,548	0,496	0,449	0,406
	0,090	0,163	0,222	0,268	0,329	0,347	0,359	0,365
	0,004	0,016	0,033	0,053	0,098	0,121	0,143	0,164
	0,0002	0,0011	0,0033	0,0072	0,0198	0,0284	0,0383	0,0494
		0,0001	0,0003	0,0007	0,0030	0,0050	0,0077	0,0111
				0,0001	0,0004	0,0007	0,0012	0,0020
						0,0001	0,0002	0,0003

Локальная теорема Муавра-Лапласа. Если вероятность p наступления событияАв каждом испытании постоянна и отлична от 0 и 1, то вероятность 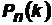того, что событие Апроизойдет kраз в nнезависимых испытаниях при достаточно большом числе n, приближенно равна:

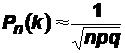φ(x), где φ 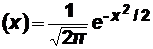и .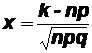

Чем больше n, тем точнее указанная приближенная формула, называемая локальной формулой Муавра-Лапласа.

Обычно этой формулой пользуются тогда, когда 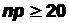. Значения функции φ(x) приведены в Приложении №1. Отметим

свойства функцииφ(x):

1) φ(-x)=φ(x), т.е. функция является четной;

2) функция φ(x) является монотонно убывающей при положительных значениях x, причем 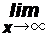φ(x)=0.

Задачи для самостоятельного решения:

6.1Найти вероятности числа выпадений гербов при бросаниитрёх монет.

6.2Найти вероятность числа появлений «шестерки» при бросании трёх костей.

6.3В ящике находятся 6белых и 9красных шаров. Из ящика извлекают шар, фиксируют его цвет, после чего возвращают шар обратно в ящик. Указанный опыт повторяют трижды. Какова вероятность того, что из трех извлеченных при этом шаров ровно два окажутся белыми?

6.4В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене: 1) не будут проданы 5 пакетов; 2) будет продано:

а) менее 2 пакетов; б) не более 2; в) хотя бы 2; г) наивероятнейшее число пакетов.

6.5Отрезок разделен на 4равные части. На отрезок брошено

наудачу8точек. Найти вероятность того, что на каждую из четырех частей отрезка попадет по две точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

6.6Проблема Джона Смита. Одинаковы ли шансы на успех у трех человек: для первого – получить хотя бы одну «6» при 6 бросках игральной кости; для второго – получить хотя бы две «6» при 12бросках; для третьего – хотя бы три «6» при 18 бросках?

6.7(Задача Банаха) Некто носит с собой две коробки спичек. Время от времени он вынимает спичку из наугад выбранной коробки. В очередной раз выбранная коробка оказывается пустой. Чему равна вероятность того, что в другой коробке в этот момент осталось kспичек?

6.8Два человека подбросили по 3монеты каждый. Какова вероятность того, что у них будет одинаковое количество гербов?

6.9Вероятность выигрыша по одному лотерейному билету равна 0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью, не меньшей 0,95?

6.10Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна0,01. Найти вероятность того, что из проданных пар обуви будет возвращено:

а) ровно 4 пары; б) ровно 5 пар.

6.11Игра состоит в набрасывании колец на колышек. Игрок получает 6колец и бросает кольца до первого попадания. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным, если вероятность попадания при каждом броске равна 0,1.

6.12Изделия некоторого производства содержат 0,1%брака. Какова вероятность, что из 5000 изделий:

а) хотя бы одно бракованное; б) не менее 3бракованных?

6.13Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,02%. Найти вероятность того, что из этой партии изделий:

1) будет повреждено: а)3; б) по крайней мере3;

2) не будет повреждено: а)9997; б) хотя бы 9997.

6.14На экономическом факультете на первом курсе учится 1825студентов.Найти вероятность того, что 15 октября является днем рождения одновременно четырёх студентов.

6.15Для данного баскетболиста вероятность забросить мяч в корзину при броске равна 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.

6.16Стрелок сделал 80 выстрелов; вероятность попадания при каждом выстреле равна 0,7. Найти вероятность того что:
а) стрелок попадает 56 раз; б) число попаданий будет заключено между 50 и 60.

6.17Контрольную работу по теории вероятностей успешно выполняют в среднем 70% студентов. Какова вероятность того, что из 200 студентов работу успешно выполнят:

а)150 студентов; б) не менее 100 студентов; в) не более 150 студентов?

6.18Какое число nраз нужно подбросить симметричную монету, чтобы вероятность хотя бы одного появления герба была больше 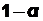=0,99?

6.19При каждом выстреле с вероятностью 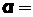0,7поражается цель, а с вероятностью 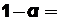0,3 – нет. Какое число nвыстрелов нужно произвести для того, чтобы вероятность хотя бы одного поражения цели была больше 0,99?

6.20Какое число nраз нужно наугад выбрать одно из 10000изделий (каждый раз возвращая его на место), чтобы вероятность хотя бы один раз выбрать некачественное изделие была больше 0,999?

6.21В задаче на схему Бернулли найти значение 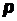, при котором вероятность 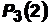достигает максимума, и вычислить этот максимум.