Тема 3: вероятностные модели

Теория вероятностей изучает математические модели случайных явлений, но не всех, а только таких, которые обладают свойством статистической устойчивости относительных частот. В любой вероятностной модели считаются известными все возможные неразложимые исходы эксперимента. Однако множество таких исходов может быть конечным или бесконечным. В зависимости от этого строят различные вероятностные модели.

Аксиомы, задающие само понятие вероятности:

А.1Каждому событиюАпоставлено в соответствие неотрицательное число P(А), называемое вероятностью события А: 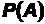≥0.

Так как любое событие есть множество, то вероятность события есть функция, заданная на множестве.

А.2Вероятность достоверного события равна1: .

А.3Вероятность суммы несовместных событий равна сумме вероятностей этих событий, т.е. если =Ø( I≠ j),то

= .

Из аксиом А.1–А.3 следуют основные свойства вероятности:

1)Если Ø – невозможное событие, то (Ø)=0.

2) .

3)При справедливо неравенство: ≤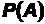

4)Для любых двух событийА и В: .

(это свойство называется расширеннойформулой сложения).

5)Для любых событий , ,…, : .

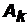Теорема.Сумма вероятностей событий , ,…, , 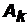образующих полную группу, равна единице: .

Модель Лапласа (классическая модель): число равновозможных результатов – конечно.

.

Эта формула дает классическое определение вероятности: вероятность случайного события А вычисляется как отношениечисла элементарных исходов, благоприятствующих появлению А, к общему числу возможных элементарных исходов.

Обычная схема подсчета вероятности случайного событияАдля описанной выше модели выглядит так:

1)выбирается (с обоснованием равновозможности элементарных исходов);

2)подсчитывается количество элементов в ;

3)подсчитывается количество элементов вА;

4)вычисляется вероятность .

Для испытаний, число равновозможных исходов в которых – бесконечностроится геометрическая модель: элементарные исходы интерпретируются как выбор наудачу точки из некоторого множества в . Предполагается, что множество имеет некоторую геометрическую форму, которую можно каким-либо образом измерить (определить длину – в , либо вычислить площадь – в , объем – в и т.п.). Событием называется следующее: выбранная точка принадлежит заданной части фигуры. Вероятность такого события определяется как отношение меры (обозначение mes) части фигурыА к мере всей фигуры Ω: . В описанной геометрической модели остаются в силе все аксиомы А.1 – А.3, соответственно выполняются все свойства 1 – 5.

Принцип практической уверенности:

В статистике все события подразделяют на «маловероятные», «высоковероятные» и «типичные». Интуитивно понятно: если известно, что данное событие имеет вероятность, близкую к нулю, то, скорее всего, в единичном испытании оно не произойдет. Если же вероятность события близка к единице, то практически можно считать, что в единичном испытании это событие наступит.

Естественно возникает вопрос о значении порогового уровня для слишком малой и слишком большой вероятности. Экономисты традиционно в качестве порогового значения, отделяющего «малые» вероятности используют (пятипроцентный уровень значимости). Для «больших» вероятностей такое значение равно

1-α=0,95. Соответственно, если вероятность случайного событияАудовлетворяет условию: ≤ ≤ 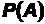, то такое событие считается «типичным», следовательно, его наступление в эксперименте можно объяснить случайностью. Если вероятность случайного событияАменьше 0,05, но, тем не менее, событие произошло, то это можно считать подозрительным фактом; аналогично подозрительным будет и ненаступление «высоковероятного» события.

Задачи для самостоятельного решения:

3.1Имеются карточки, на каждой из которых – цифра (от 0 до 9). Чему равна вероятность, извлекая наудачу 3 карточки, получить число 129? а) выборка без возвращения; б) с возвращением.

3.2Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: а) все грани неокрашенные; б) одну окрашенную грань; в)две окрашенные грани; г) три окрашенные грани; д) четыре окрашенные грани.

3.3В коробке лежат одинаковые по внешнему виду конфеты: 2 с орешками и 2 с мармеладом. Возьмем наудачу 2конфетки. Вероятность какого из событий больше: того, что обе конфеты с одинаковой начинкой или что с разной?

3.4Бросаются два игральных кубика. Какова вероятность того, что: а) сумма выпавших очков равна 7; б) сумма выпавших очков меньше 4; в) сумма равна 7, а произведение не превосходит 10?

3.5Можно ли объяснить случайностью, что в наудачу составленной стопке из 10-ти дисков оказались рядом: а) два определенных диска; б) три определенных диска?

3.6Можно ли объяснить случайностью, что в группе из 5 человек, у всех совпадают дни рождения?

3.7Из колоды карт (52 шт.) вынимаются наудачу 4 карты. Какова вероятность того, что они: а)одной масти; б)одного значения; в)все разных значений; г)все разных мастей?

3.8В ящике 5 красных и8 белых шаров.Наудачу извлекается 3 шара. Какова вероятность того, что среди них: а)ровно 1 белый шар; б)ни одного белого; в)все шары – белые; г)красных больше, чем белых?

3.9Светофор горит 60 сек. зеленым светом и по 30 сек. – красным и желтым. Какова вероятность того, что случайной машине:

а) не придется ждать у светофора; б) придется ждать более 20 сек.? (ехать можно только на зеленый свет).

3.10Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, а второго – два часа.

3.11Два приятеля договорились встретиться между 17 и 18 часами. Каждый приходит наугад и ждет 10 минут. Какова вероятность встречи?

3.12Считают, что дневная выручка магазина X принимает значения от 20 тыс. руб. до 80 тыс. руб. Найти вероятности событий:

А – выручка магазина за один день больше 40 тыс. руб.;

B – выручка магазина за два дня больше 80 тыс. руб.;

C– выручка магазина за три дня больше 120 тыс. руб.

3.13На дно колодца квадратного сечения поставим ведро, стенки которого касаются стенок колодца. Какова вероятность того, что, бросая наугад камешек, мы попадем в ведро?

3.14В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью T. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньшеt(t<T). Найти вероятность того, что сигнализатор сработает за время T, если каждое из устройств пошлет по одному сигналу.

3.15Какова вероятность того, что сумма двух взятых наугад положительных чисел, каждое из которых меньше либо равно единицы, не превзойдёт 1, а их произведение будет меньше либо равно ?

3.16Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет не больше единицы, а частное x/y не больше двух.

3.17Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найти вероятность того, что сумма x+y не превышает единицы, а произведение xy не меньше 0,09.

3.18Код домофона состоит из восьми цифр, которые могут повторяться. Какова вероятность того, что, случайно набирая цифры, можно угадать нужный код?

3.19Двое друзей, Алексей и Вадим, стоят в очереди из 8 человек. Найти вероятность того, что Алексей и Вадим стоят рядом.

3.20Из колоды в 36 карт извлекаются наудачу 4 карты. Какова вероятность событий: A – все извлеченные карты пиковой масти, B – среди этих четырех карт окажется хотя бы один король?

3.21Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трёх наугад выбранных вопросов студент знает: а)3 вопроса; б)2 вопроса; в)1 вопрос.

3.22Сколько раз нужно бросить игральную кость, чтобы с вероятностью 0,6 хотя бы один раз выпало 6 очков?

3.23В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятности следующих событий: а) выигрыш выпадет на все 5 билетов; б) выигрыш выпадет хотя бы на один билет; в) выигрыш выпадет на два билета.

3.24В ящике 20 деталей, 4 из них – нестандартные. Какова вероятность того, что среди 6 наугад взятых деталей нестандартных не окажется?

3.25Найти вероятность того, что 30 студентов одной группы родились: а) в разные дни года (в году 365 дней); б) в один день года; в) 8 марта; г) в разные месяцы года; д) в сентябре; е) в разные дни сентября.

3.26Какова вероятность того, что произвольно взятое трёхзначное число делится на 3?

3.27Какова вероятность, что два определенных студента будут направлены на практику в город C, если в наличие имеется 5 мест в город A, 8 – в город B и 7 – в город C?

3.28В круг радиуса r наудачу брошена точка. Какова вероятность того, что эта точка окажется внутри вписанного в круг правильного треугольника?

3.29На отрезке наудачу выбраны два числа и . Найти вероятность того, что эти числа удовлетворяют неравенствам .

3.30Наудачу выбирают два числа из промежутка . Какова вероятность того, что их сумма заключена между и 1?

3.31Дано шесть карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что: а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки; б) получится слово МОЛНИЯ, если наугад одна за другой выбираются шесть карточек и располагаются в ряд в порядке появления.