Часть 1. теория вероятностей
ЧАСТЬ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ТЕМА 7: ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
Пусть производится независимых испытаний, причём в первом испытании вероятность появления события
независимых испытаний, причём в первом испытании вероятность появления события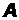 равна
равна  , во втором -
, во втором -  , … , в
, … , в  -ом испытании -
-ом испытании -  ; вероятности непоявления события
; вероятности непоявления события 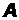 соответственно равны
соответственно равны ,
,  , … ,
, … ,  . Обозначим
. Обозначим 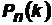 - вероятность появления события
- вероятность появления события 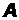 в
в  независимых испытаниях ровно
независимых испытаниях ровно  раз.
раз.
Производящей функцией вероятностей 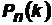 называют функцию, определяемую равенством:
называют функцию, определяемую равенством:
 .
.
Вероятность 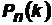 того, что в
того, что в  независимых испытаниях, в первом из которых вероятность появления события
независимых испытаниях, в первом из которых вероятность появления события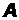 равна
равна  , во втором -
, во втором -  и т.д., событие
и т.д., событие 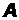 появится ровно
появится ровно  раз, равна коэффициенту при
раз, равна коэффициенту при  в разложении производящей функции по степеням
в разложении производящей функции по степеням  .
.
Например, если  , то
, то
 .
.
Производящую функцию можно применять и для определения вероятностей 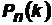 в схеме Бернулли.
в схеме Бернулли.
Кроме того, производящая функция используется и для определения вероятностей в случае когда в различных испытаниях появляются различные события: в первом испытании событие  , во втором – событие
, во втором – событие  и т.д. Изменяется лишь толкование коэффициентов при различных степенях
и т.д. Изменяется лишь толкование коэффициентов при различных степенях  . Например, в приведённом выше разложении коэффициент
. Например, в приведённом выше разложении коэффициент  определяет вероятность появления двух событий
определяет вероятность появления двух событий  и
и  .
.
Задачи для самостоятельного решения:
7.1Из двух орудий произведён залп по цели. Вероятность попадания в цель для первого орудия равна 0,8, для второго – 0,9. Найти вероятности следующих событий: а)два попадания в цель; б)одно попадание; в)ни одного попадания; г)не менее одного попадания.
7.2Четыре элемента вычислительного устройства работают неза-висимо. Вероятность отказа первого элемента за время  равна 0,2, второго – 0,25, третьего – 0,3 и четвёртого – 0,4. Найти вероятность того, что за время
равна 0,2, второго – 0,25, третьего – 0,3 и четвёртого – 0,4. Найти вероятность того, что за время  откажут: а) 4 элемента; б) 3элемента; в)ни один элемент; г)не более двух элементов.
откажут: а) 4 элемента; б) 3элемента; в)ни один элемент; г)не более двух элементов.
7.3Две батареи по 3орудия каждая производят залп по цели. Цель будет поражена, если каждая из батарей даст не менее двух попаданий. Вероятности попадания в цель орудиями первой батареи равны 0,4; 0,5; 0,6, второй – 0,5; 0,6 и 0,7. Найти вероятность поражения цели при одном залпе из двух батарей.
ПОДГОТОВКА И ПРОВЕДЕНИЕ КОНТРОЛЬНОЙ РАБОТЫ
ПО ТЕМЕ «СЛУЧАЙНЫЕ СОБЫТИЯ»
1.Студент знает 20из 30 вопросов к зачету по теории вероятностей и математической статистике. Оцените его шансы успешно сдать зачет, если для сдачи зачета необходимо знать хотя бы один из двух вопросов билета.
2.Взят кредит на год. Время закупки и доставки товара оценивают от 3до 5месяцев, время реализации – от 4до 8месяцев. Какова вероятность несвоевременного возврата кредита?
3.Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделие первого вида будет признано качественным равна0,9; для изделия второго вида такая вероятность равна 0,7; для изделий третьего вида – 0,5. Изделий каждого вида одинаковое количество. Найти вероятность того, взятое наудачу изделие будет признано качественным.
4.Статистика показывает, что10%открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из шести малых предприятий не более двух в течение года прекратят свою деятельность.
5.У Бабы Яги в избушке живут таракашки – 1000штук. Кощей Бессмертный подарил бабусе, лично им изобретенное, замечательное средство уничтожения тараканов. Гарантия успешного воздействия Кощеем оценивается весьма высоко – 99,9%. Реально ли выжить трем таракашкам?
Ответы:
1.0,896; 2.1/16; 3.0,7. 4.0,984; 5.0,061.
Приложение №1
Значение функции 
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Приложение №2
Значения функции Лапласа 
  |  |  |  |  |  |  |  |
| 0,00 | 0,5000 | 0,32 | 0,6255 | 0,64 | 0,7389 | 0,96 | 0,8315 |
| 0,01 | 0,33 | 0,65 | 0,97 | ||||
| 0,02 | 0,34 | 0,66 | 0,98 | ||||
| 0,03 | 0,35 | 0,67 | 0,99 | ||||
| 0,04 | 0,36 | 0,68 | 1,00 | ||||
| 0,05 | 0,37 | 0,69 | 1,01 | ||||
| 0,06 | 0,38 | 0,70 | 1,02 | ||||
| 0,07 | 0,39 | 0,71 | 1,03 | ||||
| 0,08 | 0,40 | 0,72 | 1,04 | ||||
| 0,09 | 0,41 | 0,73 | 1,05 | ||||
| 0,10 | 0,42 | 0,74 | 1,06 | ||||
| 0,11 | 0,43 | 0,75 | 1,07 | ||||
| 0,12 | 0,44 | 0,76 | 1,08 | ||||
| 0,13 | 0,45 | 0,77 | 1,09 | ||||
| 0,14 | 0,46 | 0,78 | 1,10 | ||||
| 0,15 | 0,47 | 0,79 | 1,11 | ||||
| 0,16 | 0,48 | 0,80 | 1,12 | ||||
| 0,17 | 0,49 | 0,81 | 1,13 | ||||
| 0,18 | 0,50 | 0,82 | 1,14 | ||||
| 0,19 | 0,51 | 0,83 | 1,15 | ||||
| 0,20 | 0,52 | 0,84 | 1,16 | ||||
| 0,21 | 0,53 | 0,85 | 1,17 | ||||
| 0,22 | 0,54 | 0,86 | 1,18 | ||||
| 0,23 | 0,55 | 0,87 | 1,19 | ||||
| 0,24 | 0,56 | 0,88 | 1,20 | ||||
| 0,25 | 0,57 | 0,89 | 1,21 | ||||
| 0,26 | 0,58 | 0,90 | 1,22 | ||||
| 0,27 | 0,59 | 0,91 | 1,23 | ||||
| 0,28 | 0,60 | 0,92 | 1,24 | ||||
| 0,29 | 0,61 | 0,93 | 1,25 | ||||
| 0,30 | 0,62 | 0,94 | |||||
| 0,31 | 0,63 | 0,95 |
 |  |  |  |  |  |  |  |
| 1,26 | 0,8962 | 1,59 | 0,9441 | 1,92 | 0,9726 | 2,50 | 0,9938 |
| 1,27 | 1,60 | 1,93 | 2,52 | ||||
| 1,28 | 1,61 | 1,94 | 2,54 | ||||
| 1,29 | 1,62 | 1,95 | 2,56 | ||||
| 1,30 | 1,63 | 1,96 | 2,58 | ||||
| 1,31 | 1,64 | 1,97 | 2,60 | ||||
| 1,32 | 1,65 | 1,98 | 2,62 | ||||
| 1,33 | 1,66 | 1,99 | 2,64 | ||||
| 1,34 | 1,67 | 2,00 | 2,66 | ||||
| 1,35 | 1,68 | 2,02 | 2,68 | ||||
| 1,36 | 1,69 | 2,04 | 2,70 | ||||
| 1,37 | 1,70 | 2,06 | 2,72 | ||||
| 1,38 | 1,71 | 2,08 | 2,74 | ||||
| 1,39 | 1,72 | 2,10 | 2,76 | ||||
| 1,40 | 1,73 | 2,12 | 2,78 | ||||
| 1,41 | 1,74 | 2,14 | 2,80 | ||||
| 1,42 | 1,75 | 2,16 | 2,82 | ||||
| 1,43 | 1,76 | 2,18 | 2,84 | ||||
| 1,44 | 1,77 | 2,20 | 2,86 | ||||
| 1,45 | 1,78 | 2,22 | 2,88 | ||||
| 1,46 | 1,79 | 2,24 | 2,90 | ||||
| 1,47 | 1,80 | 2,26 | 2,92 | ||||
| 1,48 | 1,81 | 2,28 | 2,94 | ||||
| 1,49 | 1,82 | 2,30 | 2,96 | ||||
| 1,50 | 1,83 | 2,32 | 2,98 | ||||
| 1,51 | 1,84 | 2,34 | 3,00 | ||||
| 1,52 | 1,85 | 2,36 | 3,20 | ||||
| 1,53 | 1,86 | 2,38 | 3,40 | ||||
| 1,54 | 1,87 | 2,40 | 3,60 | ||||
| 1,55 | 1,88 | 2,42 | 3,80 | ||||
| 1,56 | 1,89 | 2,44 | 4,00 | ||||
| 1,57 | 1,90 | 2,46 | 4,50 | ||||
| 1,58 | 1,91 | 2,48 | 5,00 |
Приложение №3.
Значения функции Пуассона 
 m m | 0,5 | 1,5 | 2,5 | |||
| 0,60653 | 0,36788 | 0,22313 | 0,13534 | 0,08208 | 0,04979 | |
| 0,30327 | 0,36788 | 0,33470 | 0,27067 | 0,20521 | 0,14936 | |
| 0,07582 | 0,18394 | 0,25102 | 0,27067 | 0,25652 | 0,22404 | |
| 0,01264 | 0,06131 | 0,12551 | 0,18045 | 0,21376 | 0,22404 | |
| 0,00158 | 0,01533 | 0,04707 | 0,09022 | 0,13360 | 0,16803 | |
| 0,00016 | 0,00307 | 0,01412 | 0,03609 | 0,06680 | 0,10082 | |
| 0,00001 | 0,00051 | 0,00353 | 0,01203 | 0,02783 | 0,05041 | |
| 0,00007 | 0,00076 | 0,00344 | 0,00994 | 0,02160 | ||
| 0,00001 | 0,00014 | 0,00086 | 0,00311 | 0,00810 | ||
| 0,00002 | 0,00019 | 0,00086 | 0,00270 | |||
| 0,00004 | 0,00022 | 0,00081 | ||||
| 0,00005 | 0,00022 | |||||
| 0,00001 | 0,00006 | |||||
| 0,00001 | ||||||
 m m | 3,5 | 4,5 | 5,5 | |||
| 0,03020 | 0,01832 | 0,01111 | 0,00674 | 0,00409 | 0,00248 | |
| 0,10569 | 0,07326 | 0,04999 | 0,03369 | 0,02248 | 0,01487 | |
| 0,18496 | 0,14653 | 0,11248 | 0,08422 | 0,06181 | 0,04462 | |
| 0,21579 | 0,19537 | 0,16872 | 0,14037 | 0,11332 | 0,08924 | |
| 0,18881 | 0,19537 | 0,18981 | 0,17547 | 0,15582 | 0,13385 | |
| 0,13271 | 0,15629 | 0,17083 | 0,17547 | 0,17140 | 0,16062 | |
| 0,07710 | 0,10420 | 0,12812 | 0,14622 | 0,15712 | 0,16062 | |
| 0,03855 | 0,05954 | 0,08236 | 0,10444 | 0,12345 | 0,13768 | |
| 0,01687 | 0,02977 | 0,04633 | 0,06528 | 0,08487 | 0,10326 | |
| 0,00656 | 0,01323 | 0,02316 | 0,03627 | 0,05187 | 0,06884 | |
| 0,00230 | 0,00529 | 0,01042 | 0,01813 | 0,02853 | 0,04130 | |
| 0,00073 | 0,00192 | 0,00426 | 0,00824 | 0,01426 | 0,02253 | |
| 0,00021 | 0,00064 | 0,00160 | 0,00343 | 0,00654 | 0,01126 | |
| 0,00006 | 0,00020 | 0,00055 | 0,00132 | 0,00277 | 0,00520 | |
| 0,00001 | 0,00006 | 0,00018 | 0,00047 | 0,00109 | 0,00223 | |
| 0,00002 | 0,00005 | 0,00016 | 0,00040 | 0,00089 | ||
| 0,00005 | 0,00014 | 0,00033 | ||||
| 0,00001 | 0,00004 | 0,00012 | ||||
| 0,00001 | 0,00004 | |||||
| 0,00001 | ||||||
ЧАСТЬ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
