Корреляционный анализ. Функциональная, статистическая и корреляционная зависимости.
На практике часто возникает необходимость выявления и количественного описания связей между несколькими признаками. Описание связей и нахождение тесноты и направления этих связей изучается в теории корреляции.
Изучение связи необходимо при решении задач прогнозирования и управления.
Функциональной зависимостью назовем зависимость, при которой каждому значению признака Х соответствует строго определенное значение признака Y:Х 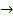 Y
Y
Статистической зависимостью между признаками Х и Y называют зависимость, при которой каждому значению одного из них соответствует распределение другого признака: Х 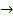 y1, y2, … yn
y1, y2, … yn
Корреляционнойзависимостью между признаками Х и Y называется зависимость, при которой каждому значению одного признака соответствует среднее значение другого:Х 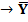 x.
x.
Корреляционная зависимость может быть линейной и криволинейной.
Основные положения корреляционного анализа. Корреляционные таблицы.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую. Предпосылкикорреляционного анализа следующие: 1) переменные величины должны быть случайными; 2) случайные величины должны иметь совместное нормальное распределение.
Корреляционной таблицейназовем таблицу, в которой указана частота пары (xi;yi)
| yi хi | y1 | y2 | … | yn | Сумма |
| x1 | n11 | n12 | … | … | |
| x2 | n12 | n21 | … | … | |
| … | … | ||||
| xn | nn1 | nn2 | … | ||
| Сумма | n |
Выборочное уравнение регрессии. Коэффициент регрессии.
Уравнением регрессии называют уравнение вида 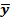 x=
x= 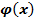 или
или 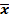 y =
y = 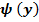
Рассмотрим линейную корреляционную зависимость. Она имеет уравнение вида: 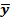 x=ax+b, где a – выборочный коэффициент регрессии.
x=ax+b, где a – выборочный коэффициент регрессии.
Выборочным уравнением прямой линии регрессииназывается уравнениевида:
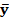 x –
x – 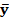 = rb
= rb 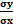 (x-
(x-  )
)
Выборочный коэффициент корреляции, его свойства.
Выборочным линейным коэффициентом корреляцииназывается число, показывающее тесноту и направление связи между двумя признаками Х и У.
rb= 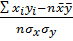
(∑ xi yi – n 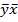 )/ ( n
)/ ( n 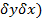
Свойства коэффициента корреляции:
1.-1≤rb≤1
2.Если rb 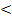 0, то связь между X и Yобратная;
0, то связь между X и Yобратная;
3.Если rb 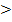 0, то связь между X и Yпрямая;
0, то связь между X и Yпрямая;
4.Если 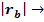 1, то связь между X и Y достаточно тесная;
1, то связь между X и Y достаточно тесная;
5.Если 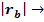 0,то связь очень слабая.
0,то связь очень слабая.
Регрессионный анализ.
Регрессионный анализ — это статистический метод исследования зависимости случайной величины Уот переменных (аргументов) хj (j = 1, 2,..., k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения хj.
Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу.
Бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа.
Если зависимая переменная является категориальной c тремя и более категориями, то подходящим методом будет мультиномиальная логистическая регрессия.
Порядковую регрессию можно использовать, когда зависимые переменные относятся к порядковой шкале.
Нелинейные связи между переменными, которые относятся к интервальной шкале можно анализировать с помощью нелинейной регрессии.
