Метод наибольшего правдоподобия.

Пусть Х –дискретная случайная величина, которая в результате испытаний принимает значение х₁,х₂…х_n.

Предположим, что нам известен закон распределения этой величины, который определяется параметром θ, но значение этого параметра неизвестно. Найдём точечную оценку параметра θ.

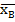– М(Х)

D_B–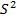

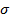_B– S

Пусть Р(х_i, θ) – вероятность того, что в результате испытания величина примет значение х_i.

Функцией правдоподобия ДСВ называется функция, которая определяется формулой:

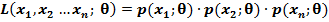
В качестве точечной оценки параметра θ примем величину, равную θ^*= θ(x₁,x₂…x_n), L 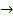max.

Т.к. функция L и lnLдостигает максимума при одном и том же значении θ, то удобно искать максимум 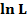– логарифмическая функция правдоподобия.

Алгоритм нахождения максимального значения этой функции:

1.найти частную производную: ;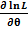

2.приравнять её к нулю и найти критические точки;

3.найти вторую частную производную: ;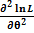

4.найти значение 2-ой производной в критических точках. Если она 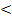0 – то точка максимума, если 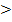0 – точка минимума.

Достоинства этого метода в том, что полученные оценки состоятельные и распределены нормально при большом числе n.

Для НСВ с известным видом плотности распределения f(x) и неизвестным параметром функция правдоподобия имеет вид: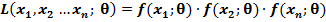

46. Условные варианты. Метод произведений для вычисления выборочных средней и дисперсии.

Условными называются варианты, определяемы равенством: 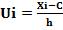, где h – шаг варьирования, т.е. разница между соседними вариантами, аС – ложный ноль (новое начало отсчёта).

Метод произведений даёт удобный способ вычисления условных моментов различных порядков с равноотстоящими вариантами. Но на практике, как правило, данные наблюдений не являются равноотстоящими. Чтобы привести их к равноотстоящим, необходимо интервал разбить на несколько равных частичных интервалов, затем найти середины этих интервалов. В качестве частоты принимают общее число первоначальных вариант этого интервала. Замена первоначальных вариант серединными сопровождается ошибками. Но эти ошибки будут погашаться, т.к. они будут иметь разные знаки.

Выборочная средняя: 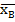= 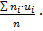h + c

Мат.ожидание:М(Х)=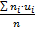

Начальные условные моменты k-ого порядка:М_k^*=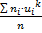

1-ого порядка:М₁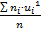^*= =М(Х)

2-ого порядка:М₂^*=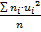

Выборочная дисперсия:D_B=(М₂* - (М₁*)²) h²

D_B= М(Х²) – М²(Х) = 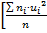– 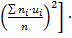h²

Выборочное среднее квадратическое отклонение: =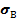

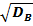
Обычные, начальные и центральные эмпирические моменты.

Обычным эмпирическим моментомпорядка j называют среднее значение j-х степеней разностей (x_i– C): М_j= = .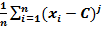

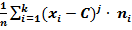Начальным эмпирическим моментом порядка kназывается величина равная:

М_к= 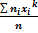,в частности М₁= 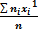= 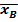,т.е. начальный эмпирический момент 1-ого порядка равен выборочному среднему.

Центральным эмпирическим моментом порядка kназывается величина равная:

m_k= 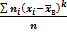,в частностиm₂ = 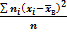=D_B, т.е. центральный эмпирический момент 2-ого порядка равен выборочной дисперсии.