Ограничения на область значений функции
Задачи, в которых применяется идея на ограничения по области значения функций, можно условно разделить на два вида:
1) задачи, где нужнонайтимаксимумилиминимум какой-либо функции (или, если это задача с параметром, например, нужно найти значения параметра, при которых будет достигаться определенное значение экстремума);
2) задачи на так называемый метод мажорант. Мажорантой функции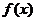 
на множествеА называется такое число М, что либо 
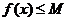для всех 
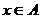, либо 
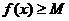для всех .
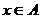Пусть дано уравнение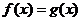 
и существует такое число М, что для любого х из области определения 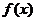и 
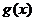получаем 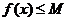и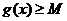 
. Тогда уравнение 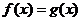эквивалентно системе 
.
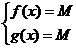В некоторых случаях может быть дана задача, где можно сравнить заданные функции с третьей, график которой проходит между ними.
Пример1
Решитьуравнение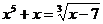 
.
Монотонное возрастание (убывание) функции
Функция 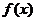называетсявозрастающейнапромежуткеD,еслидлялюбыхчисел 
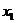и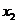 
изпромежуткаDтаких,что 
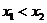,выполняетсянеравенство 
.
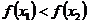Функция 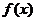называетсяубывающейнапромежуткеD,еслидлялюбыхчисел 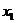и 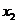изпромежуткаDтаких,что 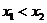,выполняетсянеравенство 
.
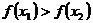Если функция возрастает или убывает на некотором промежутке, то она называется строго монотонной на этом промежутке. Если функция не возрастает или не убывает на некотором промежутке, то она называется монотонной на этом промежутке
Заметим,чтоесли 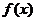–монотоннаяфункциянапромежутке 
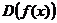,тоуравнение 
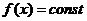неможетиметьболееодногокорнянаэтомпромежутке.
Свойства монотонных функций
(предполагается,чтовсефункцииопределенынанекоторомпромежуткеD):
- Сумманесколькихвозрастающихфункцийявляетсявозрастающейфункцией;
- Произведениенеотрицательныхвозрастающихфункцийестьвозрастающаяфункция;
- Еслифункция 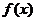возрастает и дана некоторая константа с,тофункции
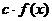, где (c>0), и 
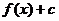такжевозрастают,афункция 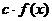, где
(c<0), убывает; - Еслифункция 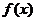возрастаетисохраняетзнак,тофункция
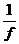убывает; - Если функция 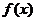возрастает и неотрицательна, то
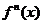, где n є N, также возрастает; - Если функция 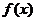возрастает и n – нечетное число, то 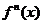также возрастает;
- Композиция
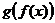возрастающихфункци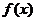й и 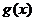такжевозрастает.
Аналогичныеутвержденияможносформулироватьидляубывающейфункции.
Использование монотонности функций при решении уравнений и неравенствоснованонаследующихтеоретическихфактах:
- Строго монотонная функция принимает каждое свое значение ровно один раз, следовательно, если дана строго монотонная функция 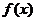и
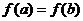, то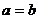 
; - Еслиоднафункциявозрастает,адругаяубываетнаодномитомжепромежутке,тографикиихлиботолькоодинразпересекутся,либовообщенепересекутся,аэтоозначает,чтоуравнение
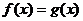имеетнеболееодногорешения; - Еслинанекоторомпромежуткеоднаизфункцийубывает(возрастает),адругаяпринимаетпостоянныезначения,тоуравнение 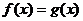либоимеетединственныйкорень,либонеимееткорней;
Таким образом, при этом способе исследуютсянамонотонностьлеваяиправаячастиуравнения, иеслиоказывается,чтофункцииудовлетворяюткакому-либоизприведенныхусловий,тонайденноеподборомрешениебудетединственнымкорнемуравнения.
Пример2
Решитьуравнение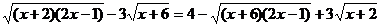 
.
Симметрия
Важно в задачах обращать внимание на четность функций, а также на другие ситуации, когда в уравнении или в системе наблюдается симметрия, так как если уравнение обладает некоторой симметрией, то такой же симметрией обладают и все его решения.
Это означает, чтоне решая уравнение и исходя лишь из соображений симметрии, мы можем заранее предвидеть некоторые свойства его решений.
Пример3
Прикакихзначенияхпараметраасистема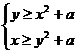 
имеетединственноерешение?