Тема 1. Вводное занятие. Функция

Понятие функции и ее аргумента

Пусть X и Y - произвольные множества. Говорят, что на Х заданафункция f, если каждому элементу х множества Х поставлен в соответствие единственный элементу множества Y. Закон соответствия обычно обозначается f : Х ®Y, y=f(x).

х называется аргументом функции у.

Областью определения функцииназывают числовое множество Х и обозначаютD(f), областью значений функции называют множество Y, состоящее из значений, которые принимает функция при подстановке чисел из множества Х, и обозначают E(f).

2. Способы задания функций

· Табличный способ.

Пример. Мы знаем значения функции для 1, 2 и 4.

х	y
	?

Можем предположить, что это функция 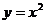и для x=3 предположить значение 9. Но это необязательно так. Например, функцией может оказаться многочлен третьей степени: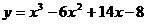

*Как найти такой многочлен, если мы знаем его степень? – Метод неопределенных коэффициентов 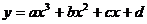. При использовании этого метода становится очевидно, что квадратный трехчлен, проходящий через заданные три точки определяется однозначно, а вот уже для многочлена третьей степени существует бесконечное множество вариантов

· Графический способ.

Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

· Аналитический способ – задание формулой y = f(x) или F(x,y)=0. В том числе можно выделить параметрический способ задания функции, когда используется параметр, через который выражаются х и y по отдельности.

Пример.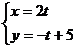

Чтобы перейти от параметрической формы к явной аналитической, необходимо исключить параметр из системы:

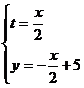Получаем прямую

· Словесный способ.

Элементарные функции

линейная ( ),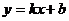

квадратичная ( ),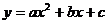

степенная ( 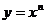, где n целое число, не равно 1),

иррациональная(степенная функций с рациональными показателями)

тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x),

обратные тригонометрические (y=arcsinx, y=arccosx, y=arctgx, y=arcctgx).

показательная ( 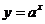,где a больше 0 и не равно 1),

логарифмическая ( 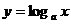, где a больше 0 и не равно 1).

Функциональные уравнения

Это такие уравнения, где неизвестной является функция.

Плоские множества

Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0).

Ее график (геометрический образ) задает некоторую границу, можно говорить, что эту границу также задает ее уравнениеy=f(x) (F(x,y)=0) – точки, координаты которых удовлетворяют уравнению составляют эту границу.

Если рассмотреть неравенство y≥f(x) (F(x,y) ≥0), оно будет задавать область на координатной плоскости, при этом нестрогость знака означает, что граница включена в образ, а строгость – что все ее точки выколоты (обычно обозначается пунктиром).

Пример. 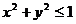- круг единичного радиуса

6. Преобразование графиков функций и других геометрических образов

Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0)

1. y=f(x)+A – график функции смещается наА единиц вверх (если А>0) или вниз (если А<0) вдоль оси Oy

2. y=f(x-A) – график функции смещается наА единиц вправо (если А>0) или влево (если А<0) вдоль оси Ox

3. y=-f(x) – график функции симметрично отображается относительно осиОх

4. y=f(-x) – график функции симметрично отображается относительно оси Oy

5. y=|f(x)| - часть графика, находившаяся выше осиОх, остается неизменной, а часть графика, находившаяся ниже этой оси, симметрично отображается относительно Ох

6. y=f(|x|) – часть графика, находившаяся правее оси Оy, остается неизменной и симметрично отражается влево относительно оси Oy.

7.y=kf(x), где k>0 – происходит растяжение графика функции вдоль оси Oy относительно осиОх (если k>1)/ сжатие (если k<1)

8. y=f(kx), где k>0 – сжатие вдоль осиОх относительно Оy (если k>1)/ растяжение (если k<1)

Поворот и замена координат

Отдельное, более сложное, чем параллельный перенос и симметрия, движение на плоскости – это поворот. Для простоты будем считать, что мы всегда делаем поворот вокруг начала координат (другие повороты – это композиция параллельных переносов и поворота вокруг (0;0)).

Поворот можно рассматривать как переход к новым осям с тем же началом координат. Оси вместе с образом поворачиваются на определенный угол по или против часовой стрелки.

Пусть 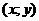- координаты точки до поворота, а 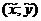- после.

Это координаты данной точки в старых осях!

Для поворота на угол 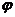против часовой стрелки действует правило:

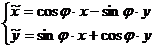(1)

Для поворота на угол 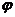по часовой стрелке действует правило:

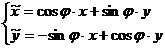
Заметим, что меняется лишь знаки перед синусами. На самом деле можно рассматривать только формулу (1), если считать, что поворот по часовой стрелке –это поворот против часовой стрелки, но на отрицательный угол. (как это делается на единичной окружности в тригонометрии).

Тема 2. Линейная функция

Векторы

Вектор – направленный отрезок (на плоскости или в пространстве).

Вектора называются равными, если они лежат на одной прямой или на параллельных прямых, направлены в одну сторону и при этом длины векторов равны.

Векторы на плоскости (как и в пространстве) можно задавать координатами. Пусть 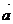- произвольный вектор на плоскости Оxy. Выберем такую точкуА плоскости, что 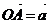. Тогда координаты точки А будут координатами вектора 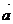. При этом будет употребляться запись 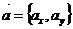, где 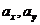- координаты точки А.

Если даны две точк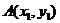и и 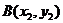, то координатами вектора 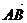будут .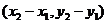

Два вектора равны тогда и только тогда, когда равны их координаты.

Операции с векторами

· модульилидлинавектора

Модулем или длиной вектора 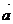называется число, равное длине отрезка, образующего данный вектор. Обозначается как 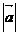. Найти его через координаты можно как .

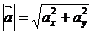• умножение вектора на число

Коллинеарность: ненулевые векторы называются коллинеарными, если они лежат на параллельных прямых (нулевой вектор считается коллинеарным любому вектору). Ненулевые векторы коллинеарны, если и только если найдется такое число k, что 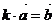, то есть 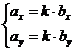. Отсюда .

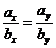• сложениевекторов
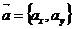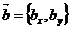• Если даны векторы с координатами и , то .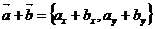

· скалярноепроизведениевекторов

Если даны векторы 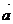и 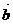, то их скалярным произведением 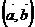называется произведение модулей этих векторов на косинус угла между ними: .

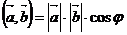Если даны два вектора с координатам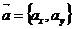и и 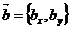, то скалярное произведение равно .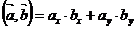