Вся теория первого семестра 2017-2018 уч.г.

Вся теория первого семестра 2017-2018 уч.г.

Тема 1. Вводное занятие. Функция

Понятие функции и ее аргумента

Пусть X и Y - произвольные множества. Говорят, что на Х заданафункция f, если каждому элементу х множества Х поставлен в соответствие единственный элементу множества Y. Закон соответствия обычно обозначается f : Х ®Y, y=f(x).

х называется аргументом функции у.

Областью определения функцииназывают числовое множество Х и обозначаютD(f), областью значений функции называют множество Y, состоящее из значений, которые принимает функция при подстановке чисел из множества Х, и обозначают E(f).

2. Способы задания функций

· Табличный способ.

Пример. Мы знаем значения функции для 1, 2 и 4.

х	y
	?

Можем предположить, что это функция 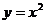и для x=3 предположить значение 9. Но это необязательно так. Например, функцией может оказаться многочлен третьей степени: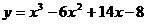

*Как найти такой многочлен, если мы знаем его степень? – Метод неопределенных коэффициентов 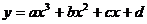. При использовании этого метода становится очевидно, что квадратный трехчлен, проходящий через заданные три точки определяется однозначно, а вот уже для многочлена третьей степени существует бесконечное множество вариантов

· Графический способ.

Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

· Аналитический способ – задание формулой y = f(x) или F(x,y)=0. В том числе можно выделить параметрический способ задания функции, когда используется параметр, через который выражаются х и y по отдельности.

Пример.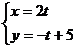

Чтобы перейти от параметрической формы к явной аналитической, необходимо исключить параметр из системы:

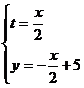Получаем прямую

· Словесный способ.

Элементарные функции

линейная ( ),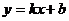

квадратичная ( ),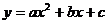

степенная ( 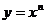, где n целое число, не равно 1),

иррациональная(степенная функций с рациональными показателями)

тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x),

обратные тригонометрические (y=arcsinx, y=arccosx, y=arctgx, y=arcctgx).

показательная ( 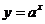,где a больше 0 и не равно 1),

логарифмическая ( 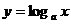, где a больше 0 и не равно 1).

Функциональные уравнения

Это такие уравнения, где неизвестной является функция.

Плоские множества

Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0).

Ее график (геометрический образ) задает некоторую границу, можно говорить, что эту границу также задает ее уравнениеy=f(x) (F(x,y)=0) – точки, координаты которых удовлетворяют уравнению составляют эту границу.

Если рассмотреть неравенство y≥f(x) (F(x,y) ≥0), оно будет задавать область на координатной плоскости, при этом нестрогость знака означает, что граница включена в образ, а строгость – что все ее точки выколоты (обычно обозначается пунктиром).

Пример. 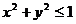- круг единичного радиуса

6. Преобразование графиков функций и других геометрических образов

Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0)

1. y=f(x)+A – график функции смещается наА единиц вверх (если А>0) или вниз (если А<0) вдоль оси Oy

2. y=f(x-A) – график функции смещается наА единиц вправо (если А>0) или влево (если А<0) вдоль оси Ox

3. y=-f(x) – график функции симметрично отображается относительно осиОх

4. y=f(-x) – график функции симметрично отображается относительно оси Oy

5. y=|f(x)| - часть графика, находившаяся выше осиОх, остается неизменной, а часть графика, находившаяся ниже этой оси, симметрично отображается относительно Ох

6. y=f(|x|) – часть графика, находившаяся правее оси Оy, остается неизменной и симметрично отражается влево относительно оси Oy.

7.y=kf(x), где k>0 – происходит растяжение графика функции вдоль оси Oy относительно осиОх (если k>1)/ сжатие (если k<1)

8. y=f(kx), где k>0 – сжатие вдоль осиОх относительно Оy (если k>1)/ растяжение (если k<1)

Поворот и замена координат

Отдельное, более сложное, чем параллельный перенос и симметрия, движение на плоскости – это поворот. Для простоты будем считать, что мы всегда делаем поворот вокруг начала координат (другие повороты – это композиция параллельных переносов и поворота вокруг (0;0)).

Поворот можно рассматривать как переход к новым осям с тем же началом координат. Оси вместе с образом поворачиваются на определенный угол по или против часовой стрелки.

Пусть 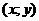- координаты точки до поворота, а 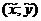- после.

Это координаты данной точки в старых осях!

Для поворота на угол 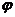против часовой стрелки действует правило:

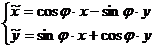(1)

Для поворота на угол 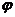по часовой стрелке действует правило:

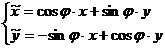
Заметим, что меняется лишь знаки перед синусами. На самом деле можно рассматривать только формулу (1), если считать, что поворот по часовой стрелке –это поворот против часовой стрелки, но на отрицательный угол. (как это делается на единичной окружности в тригонометрии).

Тема 2. Линейная функция

Векторы

Вектор – направленный отрезок (на плоскости или в пространстве).

Вектора называются равными, если они лежат на одной прямой или на параллельных прямых, направлены в одну сторону и при этом длины векторов равны.

Векторы на плоскости (как и в пространстве) можно задавать координатами. Пусть 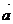- произвольный вектор на плоскости Оxy. Выберем такую точкуА плоскости, что 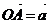. Тогда координаты точки А будут координатами вектора 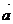. При этом будет употребляться запись 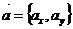, где 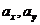- координаты точки А.

Если даны две точк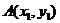и и 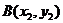, то координатами вектора 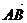будут .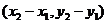

Два вектора равны тогда и только тогда, когда равны их координаты.

Операции с векторами

· модульилидлинавектора

Модулем или длиной вектора 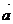называется число, равное длине отрезка, образующего данный вектор. Обозначается как 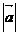. Найти его через координаты можно как .

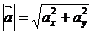• умножение вектора на число

Коллинеарность: ненулевые векторы называются коллинеарными, если они лежат на параллельных прямых (нулевой вектор считается коллинеарным любому вектору). Ненулевые векторы коллинеарны, если и только если найдется такое число k, что 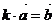, то есть 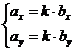. Отсюда .

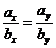• сложениевекторов
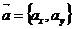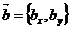• Если даны векторы с координатами и , то .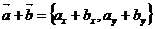

· скалярноепроизведениевекторов

Если даны векторы 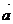и 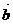, то их скалярным произведением 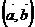называется произведение модулей этих векторов на косинус угла между ними: .

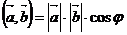Если даны два вектора с координатам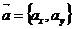и и 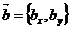, то скалярное произведение равно .

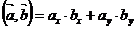Уравнениепрямой

· уравнениепрямой с угловым коэффициентом

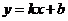
· каноническая форма уравнения прямой

Пусть нужно найти уравнение прямой по точке 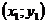и направляющему вектору 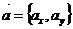, т.е. ненулевому вектору, лежащему на искомой прямой или параллельному ей.

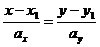
Лекция 3. Модули

Напомнимопределениемодуляиегоосновныесвойства.

Определение. Абсолютнойвеличиной (илимодулем) |х| называетсясамоэточисло, еслих‑положительноечисло; нуль, есличислох‑нуль; число, противоположноечислух, еслих‑отрицательноечисло.

Этоопределениеможнозаписатьвдругойформе:

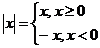
Теорема.Свойствамодулядействительногочисла:

1.│а+в│≤│а│+│в│;

2.│ав│=│а│*│в│;

3.│1/а│=1/│а│приа≠0;

4.│а-в│≥││а│-│в││.

Схемырешениярациональныхуравнений/неравенствсмодулями

1. Схема |f(x)| = c.

Прис< 0 –нетрешений.

Прис = 0 f(x) = 0.

Прис> 0 .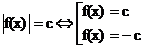

Пример 2. 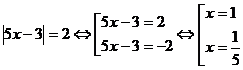. Ответ: .

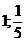2. Схема |f(x)| ≥c.

Прис≤ 0–D(f), тоестьвсечисла, прикоторыхопределенафункцияf(x).

Прис> 0 .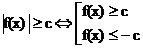

Пример 3. 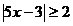. Ответ: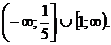

3. Схема |f(x)| ≤c.

Прис< 0–нетрешений.

Прис = 0f(x) = 0.

Прис>0 .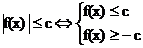

Пример 4. 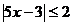. Ответ: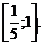

4. Схема |f(x)| = g(x).

.

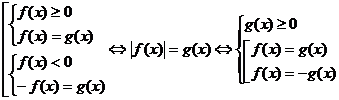Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).

5. Схема |f(x)| ≥ g(x).

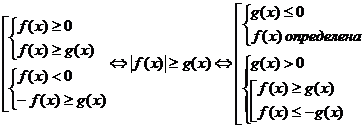
Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).

6. Схема |f(x)| ≤ g(x).

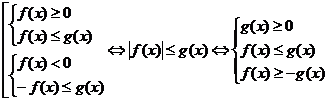
Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).

Методинтерваловдлямодулей

Применяетсявуравненияхинеравенствахтипа |f(x)| + |g(x)| = h(x) иимподобных, тоестьтам, гдеестьнесколькомодулейионинезависятдруготдруга (втомсмысле, чтонеявляютсявложенными). Вслучаевложенныхмодулейнадораскрыватьотвнешнегоквнутреннемуилинаоборот–взависимостиотвозможныхупрощений, новодномпорядке.

Схема метода интервалов для модулей. Разбиваем числовую ось точками, в которых подмодульные выражения равны нулю, на промежутки знакопостоянстваподмодульных выражений. На каждом промежутке раскрываем модули (в зависимости от знака подмодульного выражения), решаем уравнение или неравенство, пересекаем получающийся ответ с промежутком. Затем объединяем полученные на всех промежутках ответы.

Напомним:

1.y=|f(x)| - часть графика, находившаяся выше оси Ох, остается неизменной, а часть графика, находившаяся ниже этой оси, симметрично отображается относительно Ох

2. y=f(|x|) – часть графика, находившаяся правее оси Оy, остается неизменной и симметрично отражается влево относительно оси Oy.

3. |y|=f(x) – часть графика, находившаяся выше Ох остается неизменной и симметрично отражается вниз относительно Ох, а часть графика, находившаяся ниже оси Ох стирается.

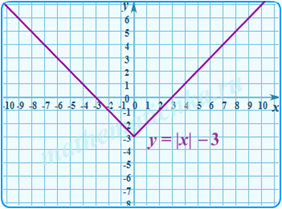
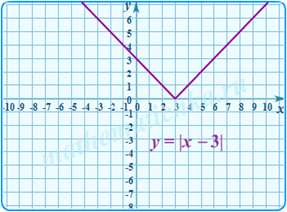
y=|x-a|

Сделаем математику красивее…

Построить множество точек, задающееся уравнением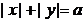

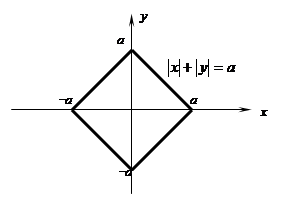
Комментарий: а–половинадиагоналиквадрата.

Геометрическийцентрквадрата– (0;0).

Чётнопохиу, тоесть, строимвпервойчетверти

иотражаемвовсечетыре.

Построить множество точек, задающеесяуравнением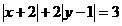

Сумма модулей

Если функция является суммой или разностью нескольких модулей, следует разбить координатную плос-кость на участки и построить часть графика на каждом из участков отдельно. Границы участков определяют-ся значениями переменных, при которых обнуляется один из модулей. Таким образом, эти границы можно найти с помощью приравнивания каждого модуля к нулю и решением соответствующего уравнения.

Пример 3.

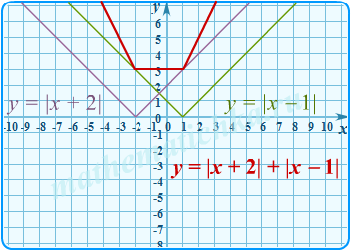
Построить график функции y = |x + 2| + |x − 1|.

Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, иследовательно, 2 уравнения, каждое из которых имеет одно решение, следовательно, 2 границы, которыми плоскость разби-та на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.

На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1|, используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участ-ках, например, при x = −3 и x = 3. На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).

Запомните:Если y1 = k1x+b1и y2 = k2x+b2, то их сумма:!

Ysum = y1+y2 = (k1+k2)x + (b1+b2)

Парабола

Определение (геометрическое). Парабола – геометрическое место точек на плоскости, равноудаленных от данной точки 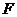, называемой фокусом, и прямой 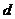, называемой директрисой. Предполагается, что .

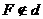Определение (аналитическое). Парабола – кривая второго порядка, задаваемая в некоторой прямоугольной системе координат уравнением ( )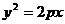

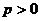Число 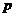называется фокальным параметром. Его геометрический смысл – расстояние между директрисой 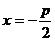и фокусом .

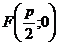Теорема. Аналитическое и геометрическое определения параболы совпадают.

Параллельный перенос параболы. Уравнение 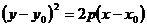задаёт ту же параболу 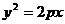с вершиной в точке .

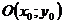Вернемся в наши стандартные оси – то есть сделаем замену :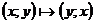

Уравнение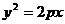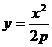
Директриса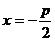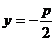
Фокус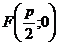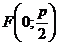

Задания, связанные с условиями на импликацию

Импликация – логическая связка, по смыслу схожая с союзами «если… то».

Импликация записывается как посылка => следствие.

Пример:

Пусть существуют множества А и В, при этом А входит в В, т.е. является его подмножеством. Тогда верна следующая логическая связка: если число 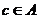, следовательно, .

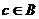Понятие обратной функции

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.

Обратная функция функции 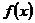{\displaystylef} обычно обозначается .

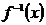Чтобы для функции 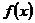найти обратную функцию 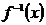, нужно в уравнении 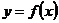вместо 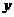подставить 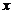, а вместо 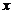— 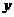и решить его относительно 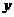(выразить 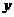через 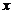). Если оно имеет более чем один корень, то функции, обратной к {\displaystylef} 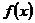, не существует.

Функция {\displaystylef(x)} 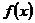обратима на некотором интервале {\displaystyle (a;b)}тогда и только тогда, когда на этом интервале она взаимно-однозначна, т.е. каждому значению аргумента соответствует ровно однозначение функции, и наоборот, каждое значение функции достигается только при одном значении аргумента.

Пример. ,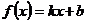

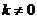
Ищем обратную: 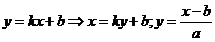. Обратная функция: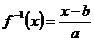

Пример.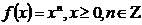

Обратная: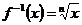

Теорема. Так как переход к обратной функции происходит с помощью замены 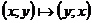, графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

Функция 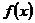{\displaystylef} является обратной к 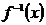. Функции 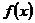{\displaystylef} и 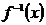называются взаимно обратными.

2. Свойства взаимно обратных функц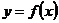ий 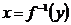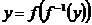и .

· и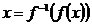

· Область определения функции 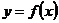совпадает с областью значений функции 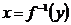и наоборот. ,

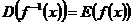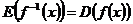
· Графики взаимно обратных функций симметричны относительно прямой .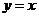

· Если 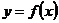возрастает, то и 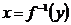возрастает, если 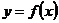убывает, то и 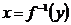убывает.

{\displaystylef^{-1}}3. Основные свойства степеней:

1) Если m и n – натуральные числа, то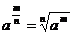

2)

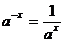
3)

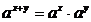
4)

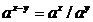
5)

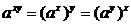
6)

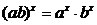
7)

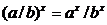
8)

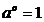
9)

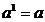
Метод рационализации

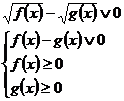
Тема 7. Гипербола

Важные термины лекции(14 штук):

Гипербола, дробно-линейная функция, асимптота, фокусы гиперболы, фокальный радиус, фокусное расстояние, эксцентриситет, каноническая для гиперболы система координат, фокальная или действительная ось, каноническое уравнение гиперболы, главные для гиперболы оси координат, центр гиперболы, основной прямоугольник гиперболы, директриса гиперболы.

Пример 1. Оптимизационная задача с использованием понятия градиента

Найти наибольшее и наименьшее значение параметра а, при котором выполняется следующая система:

Важные термины:

Линии уровня - линии, которые может задавать уравнение целевой функции с учетом значений параметра.

Градиент (от лат.gradiens, род.падеж gradientis – шагающий, растущий) – вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный скорости роста этой величины в этом направлении.

Градиент является вектором нормали, перпендикулярным линиям уровня – линии уровня будут двигаться вдоль этого вектора. Как мы знаем из лекции 2, если уравнение прямой задано в общем виде 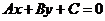, то нормальный вектор задается как .

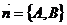Пример 2. Целочисленная оптимизационная задача

Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб.соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.

Пример 3. Задача на максимум/минимум квадратичной функции

В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t² у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t² у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?

Пример 4. Нахождение максимума/минимума некоторых функций

Найти наименьшее значение функции

Пример 5. Нахождение максимума/минимума некоторых функций

Среди всех решений системы 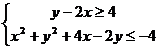найдите такое, при котором выражение 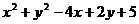принимает минимальное значение

Пример 5. Задача на движение

(Встречное движение). Два туриста отправились одновременно из пунктов A и B, расстояние между которыми 33 км, навстречу друг другу. Через 3ч 12мин расстояние между ними сократилось до 1км (они еще не встретились), а еще через 2ч 18мин первому осталось пройти до B втрое больше расстояния, чем второму до A. Найдите скорости туристов.

Пример 6. Задача на движение

Ровно в 9:00 из пункта А в пункт Б выехал автомобиль. Проехав две третьих пути, наблюдательный водитель автомобиля заметил, что мимо него в сторону пункта А проехал некий велосипедист. В тот самый момент, когда автомобиль прибыл в пункт Б, из пункта Б в пункт А выехал автобус. Когда до пункта А оставалось две пятых пути, не менее наблюдательный водитель автобуса заметил, что он поравнялся с тем самым велосипедистом. Во сколько приедет велосипедист в пункт А, если известно, что автобус прибыл в пункт А ровно в 11:00? Скорости велосипедиста, автомобиля и автобуса считать постоянными.

Пример1

Решитьуравнение .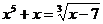

Свойства монотонных функций

(предполагается,чтовсефункцииопределенынанекоторомпромежуткеD):

• Сумманесколькихвозрастающихфункцийявляетсявозрастающейфункцией;
• Произведениенеотрицательныхвозрастающихфункцийестьвозрастающаяфункция;
• Еслифункция 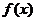возрастает и дана некоторая константа с,тофункции 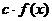, где (c>0), и 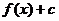такжевозрастают,афункция 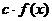, где
  (c<0), убывает;
• Еслифункция 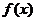возрастаетисохраняетзнак,тофункция 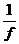убывает;
• Если функция 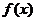возрастает и неотрицательна, то 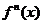, где n є N, также возрастает;
• Если функция 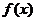возрастает и n – нечетное число, то 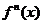также возрастает;
• Композиция 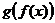возрастающихфункци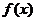й и 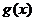такжевозрастает.

Аналогичныеутвержденияможносформулироватьидляубывающейфункции.

Использование монотонности функций при решении уравнений и неравенствоснованонаследующихтеоретическихфактах:

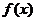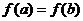• Строго монотонная функция принимает каждое свое значение ровно один раз, следовательно, если дана строго монотонная функция и , то ;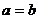
• Еслиоднафункциявозрастает,адругаяубываетнаодномитомжепромежутке,тографикиихлиботолькоодинразпересекутся,либовообщенепересекутся,аэтоозначает,чтоуравнение 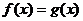имеетнеболееодногорешения;
• Еслинанекоторомпромежуткеоднаизфункцийубывает(возрастает),адругаяпринимаетпостоянныезначения,тоуравнение 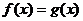либоимеетединственныйкорень,либонеимееткорней;

Таким образом, при этом способе исследуютсянамонотонностьлеваяиправаячастиуравнения, иеслиоказывается,чтофункцииудовлетворяюткакому-либоизприведенныхусловий,тонайденноеподборомрешениебудетединственнымкорнемуравнения.

Пример2

Решитьуравнение .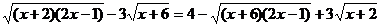

Симметрия

Важно в задачах обращать внимание на четность функций, а также на другие ситуации, когда в уравнении или в системе наблюдается симметрия, так как если уравнение обладает некоторой симметрией, то такой же симметрией обладают и все его решения.

Это означает, чтоне решая уравнение и исходя лишь из соображений симметрии, мы можем заранее предвидеть некоторые свойства его решений.

Пример3

Прикакихзначенияхпараметраасистема 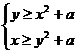имеетединственноерешение?

Вся теория первого семестра 2017-2018 уч.г.