Метод Гаусса с выбором главного элемента по столбцу

На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент 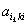при неизвестной 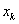в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером 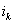, меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента 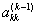. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

ПРИМЕР 1.Решение системы методом Гаусса с выбором главного элемента по столбцу.

Пусть Ax=b, где

A= 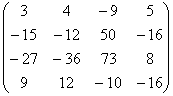, b= .

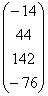Прямой ход. 1 шаг. Максимальный по модулю элемент 1-го столбца 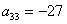. Переставим 1-ое и 3 - е уравнения местами:

A= 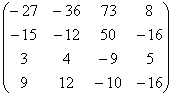, b= .

Вычислим масштабирующие множители 1 шага:

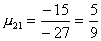
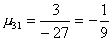
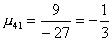
и выполним преобразование матрицы и вектора:

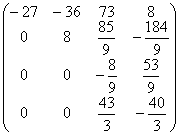A1= b1= .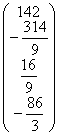

2 шаг. Вычислим масштабирующие множители 2 шага:

.

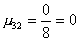
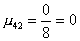Второй шаг не изменяет матриц: A2=A1, b2= b1.

3 шаг. Максимальный по модулю элемент 3 столбца 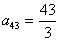. Переставим 3 и 4 уравнения местами.

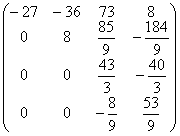A2= b2= .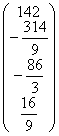

Вычислим масштабирующие множители 3 шага:

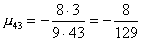
и выполним преобразование матрицы и вектора:

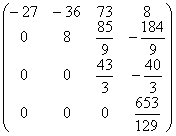A3= b3= .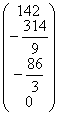

Обратный ход. Из последнего уравнения находим: 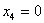. Из третьего

уравнения системы находим 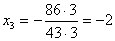. Из второго уравнения находим

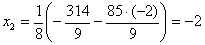. Неизвестное 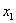находим из первого уравнения:

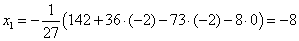
Ответ: .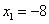

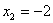
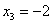
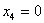% Решить систему Ax=b методом Гаусса

% Введём матрицу

A = [3,4,-9,5;-15,-12,50,-16;-27,-36,73,8;9,12,-10,-16];

% Введём правую часть

b = [-14; 44; 142; -76];

% Решим систему средствами MATLAB

x = A \ b

>>

x =	-8.0000
	-2.0000
	-2.0000
	-0.0000

Метод Холецкого

Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A= . Если разложение получено, то, как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами: и . Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:

, i = 2, 3, ..., m,

, i = 3, 4, ..., m,

...............

i = k+1, ... , m.

ПРИМЕР 2. Решение системы методом Холецкого.

Пусть

A= b= .

Находим элементы матрицы L:

Таким образом, разложение матрицы A имеет вид:

Последовательно решаем системы и . Решением 1-ой системы является вектор , а решение 2-ой системы вектор .

Ответ:

% Решить систему Ax=b методом Холецкого

% Введём матрицу

A = [81 -45 45; -45 50 -15; 45 -15 38];

% Введём правую часть

b = [531; -460; 193];

% Найдём разложение Холецкого

R = chol(A);

% R'*R*x = b

% Матрица R легко обратима

y = R' \ b;

x = R \ y;

% Проверим решение

A * x - b

>>

ans =

Метод прогонки

Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

Преобразуем первое уравнение системы к виду , где: , . Подставим полученное выражение во второе уравнение системы и преобразуем его к виду: и т.д.

На i-ом шаге уравнение преобразуется к виду: , где , .

На m-ом шаге подстановка в последнее уравнение выражения

дает возможность определить значение :

.

Значения остальных неизвестных находятся по формулам:

, i = m-1, m-2, ..., 1.

ПРИМЕР 4. Решение системы методом прогонки.

Прямой ход прогонки. Вычислим прогоночные коэффициенты:

, ,

,

, ,

,

Обратный ход прогонки. Находим значения неизвестных:

, , ,

Ответ:

.

Задание для самостоятельной работы

1. Методом Гаусса с выбором главного элемента найти решение системы уравнений:
.

2. Найти разложение матрицы:

.

3. Можно ли применять метод Холецкого к системе уравнений, матрица которой имеет вид:

.

4. Подсчитать количество арифметических действий в методе прогонки.

Вопросы

1. Что такое прямые и итерационные методы.

2. С какой целью применяют модификацию метода Гаусса - схему частичного выбора.

3. Для каких систем уравнений применяют метод Холецкого.

4. Запишите формулы для нахождения решения после приведения системы к виду.

5. Сформулируйте алгоритм метода прогонки.