Статистическое оценивание показателей надежности.
Вероятностное пространство
Определение 1. Вероятностным пространством будем называть тройку 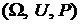 , где Ω - пространство элементарных исходов, U – алгебра событий, P – вероятность (функция на U со значениями во множестве действительных чисел R).
, где Ω - пространство элементарных исходов, U – алгебра событий, P – вероятность (функция на U со значениями во множестве действительных чисел R).
Замечание. Ω – это произвольное множество, U – алгебра событий (совокупность подмножеств множества Ω, замкнутая относительно операций сложения, умножения и разности событий ). Свойства функции P:
1) 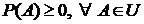
2) 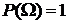
3) 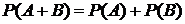 – для несовместных событий ( события А и В несовместны, если
– для несовместных событий ( события А и В несовместны, если 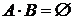
 если произойдет А , то это исключает, что произойдет В, и наоборот).
если произойдет А , то это исключает, что произойдет В, и наоборот).
Определение 2.События А и В независимы, если
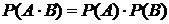 . (1)
. (1)
Определение 3.Пусть 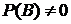 . Тогда условная вероятность наступления события А при условии, что В произошло
. Тогда условная вероятность наступления события А при условии, что В произошло 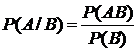 . (2)
. (2)
Пример 1. Вероятность отказа каждого элемента электрической цепи
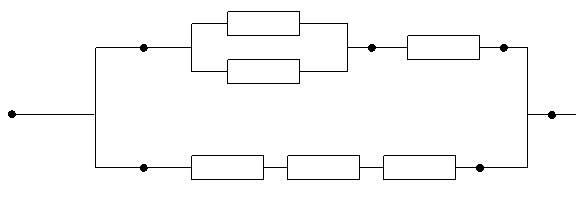
M N K
A B
E F
равна 0,1. Элементы работают независимо друг от друга. Отказ элемента – его деструкция, приводящая к разрыву соответствующего участка цепи. Найти вероятность того, что между точками А и В будет идти электрический ток.
Решение.Схема в примере – это логическая модель надежности. При последовательном соединении элементов модели удобно вычислять вероятность работы соответствующего участка (произведение вероятностей работ каждого элемента), при параллельном – отказ (произведение вероятностей отказов каждого элемента).
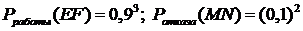 ;
; 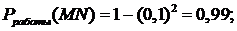
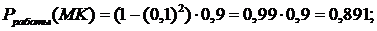
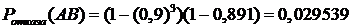 ;
; 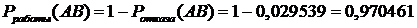 .
.
Замечание. При построении логической модели надежности каждому элементу реальной электрической цепи ставят в соответствие элемент логической модели. При этом, если элемент электрической цепи работоспособен – то ему соответствует элемент логической модели, имеющий бесконечную проводимость, а неработоспособному элементу соответствует элемент с нулевой проводимостью.
Например, электрической цепи с диодами
D1  D2 D3
D2 D3





или резисторами
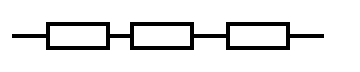 R1 R2 R3
R1 R2 R3
при отказах типа «обрыв», соответствует логическая модель

1 2 3 .
Для конденсаторов можно рассматривать два типа отказов: короткое замыкание или обрыв. Тогда имеет место следующие соответствия электрической цепи и логических моделей.
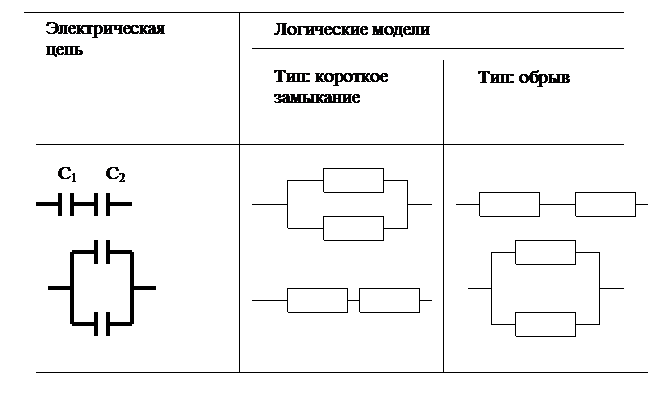
1 2
С1 2
1 2
С2 2
Пример 2. Построить логическую модель и определить вероятность безотказной работы схемы соединения конденсаторов.
Типы отказов конденсаторов:
1) короткое замыкание;
2) обрыв.
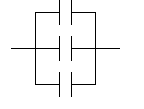
с1
с2
с3
Вероятность безотказной работы каждого 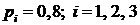 .
.
Решение.1) Логическая модель надежности: 
А В
1 2 3 .
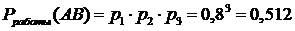 .
.
2) Логическая модель надежности:
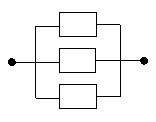
A 2 В
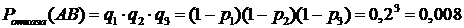 .
.
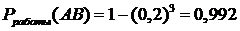 .
.
Пример 3.Найти вероятность безотказной работы схемы, логическая модель которой:
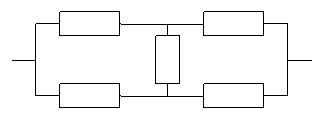
1 2
5 .
3 4
Вероятность безотказной работы каждого элемента 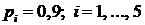 .
.
Решение.Пусть 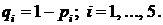 Применим метод разложения относительно особого элемента: пусть гипотеза
Применим метод разложения относительно особого элемента: пусть гипотеза  - 5-й элемент отказа,
- 5-й элемент отказа,  - 5-й элемент работоспособен.
- 5-й элемент работоспособен.
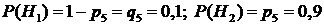 .
.
Этим гипотезам соответствуют схемы:

1 2 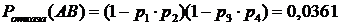
A В 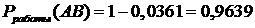 .
.
3 4
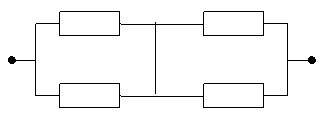
1 2
А В
3 4
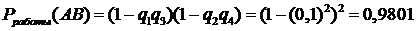 .
.
Далее по формуле полной вероятности:
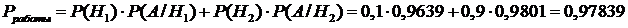 .
.
Упражнения
1.1. Найти вероятность безотказной работы схемы, логические модели которых:
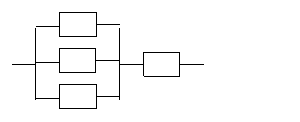 а)
а)
2 4
б)
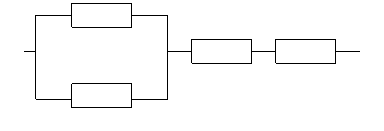
3 4
в) 
1 3
.
2 4
Вероятности безотказной работы элементов равны
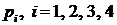 .
.
Ответ.а) 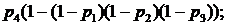
б) 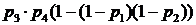 ;
;
в) 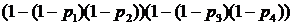 .
.
1.2. Вероятности безотказной работы каждого элемента за время Т равны 0,9. Найти вероятность безотказной работы за время Т схем, логические модели которых:
а)
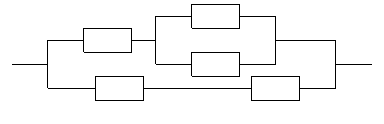
б)
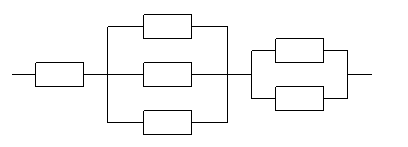
в)
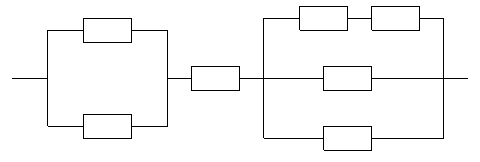
г)
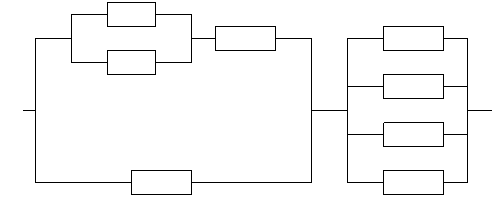
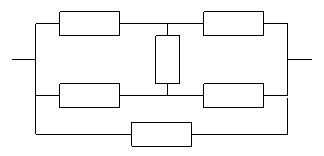
д)
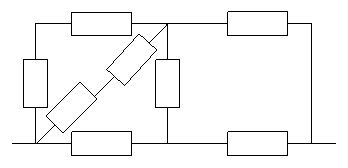 е)
е)
ж)

Ответ.а) 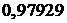 ; б) 0,890109; в) 0,8893; г) 0,989;
; б) 0,890109; в) 0,8893; г) 0,989;
д) 0,997848; е) 0,985; ж) 0,99586.
Случайные величины.
Определение 1. Пусть 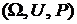 - вероятностное пространство. Действительно-значную функцию
- вероятностное пространство. Действительно-значную функцию 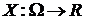 , определенную на Ω будем называть случайной величиной (для краткости СВ Х), если
, определенную на Ω будем называть случайной величиной (для краткости СВ Х), если 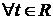 множество
множество 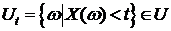 . При этом функция
. При этом функция 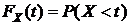 называется функцией распределения СВ Х. Если множество значений СВ Х – конечно или счетно, то СВ Х называется дискретной, если значения СВ Х целиком заполняют некоторый интервал действительной оси, то СВ Х называется непрерывной.
называется функцией распределения СВ Х. Если множество значений СВ Х – конечно или счетно, то СВ Х называется дискретной, если значения СВ Х целиком заполняют некоторый интервал действительной оси, то СВ Х называется непрерывной.
Замечание.Среди непрерывных СВ будем рассматривать абсолютно-непрерывные, а именно такие, что
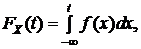 (1)
(1)
где 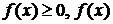 - кусочно-непрерывна.
- кусочно-непрерывна.
При этом функция 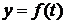 называется плотностью вероятностей СВ Х, и верны формулы:
называется плотностью вероятностей СВ Х, и верны формулы:
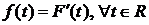 , (2)
, (2)
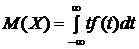 , (3)
, (3)
где М(Х) – математическое ожидание (среднее значение) СВ Х;
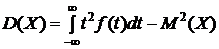 - дисперсия СВ Х (4)
- дисперсия СВ Х (4)
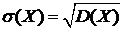 - среднее квадратическое отклонение СВ Х. (5)
- среднее квадратическое отклонение СВ Х. (5)
Для дискретной случайной величины Х, заданной законом
| Х | х1 | х2 | … | xn |
| Р | р1 | р2 | … | рn |
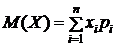 , (6)
, (6)
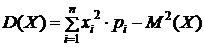 . (7)
. (7)
Определение 2.Дискретная СВ Х называется распределенной по закону Бернулли 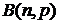 (биномиальному закону), если значения X: 0, 1, …, n и
(биномиальному закону), если значения X: 0, 1, …, n и
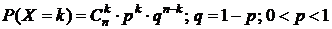 , (8)
, (8)
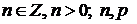 - параметры распределения.
- параметры распределения.
Замечание. 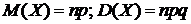 .
.
Пример 1.Система состоит из 4-х блоков, работающих независимо друг от друга. Вероятность безотказной работы любого из них за время t равна р=0,8. Для нормальной работы системы за время t необходимо, чтобы работали хотя бы 3 блока. Найти вероятность того, что: 1) система будет работать в течение времени t; 2) система откажет.
Решение. Пусть СВ Х – число работающих исправно в течение времени t блоков. Тогда по формуле (8):
1) 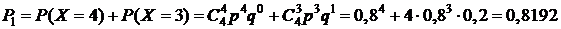 .
.
2) 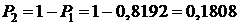 .
.
Замечание. Биномиальный закон распределений часто применяется при статистическом контроле качества изделий, когда мало сведений о природе и поведении изделий и их нужно разделить на исправные и неисправные.
Определение 3. Дискретная СВ Х называется распределенной по закону Пуассона 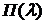 , если значения
, если значения
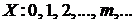 и
и 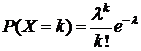 ; (9)
; (9)
где 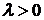 - параметр распределения.
- параметр распределения.
Замечание. 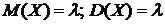 .
.
Теорема 1 (теорема Пуассона).Пусть СВ Х распределена по закону Бернулли с параметром р. Пусть 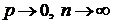 , так что
, так что 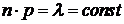 , тогда
, тогда
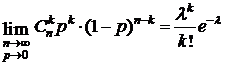 . (10)
. (10)
Замечание. Из теоремы 1 следует, что распределение Пуассона 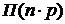 – предельный случай биномиального распределения при
– предельный случай биномиального распределения при 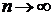 . Если n – велико, а р мало, то вместо формулы (8) для распределения B(n, p) используют формулу (9), где
. Если n – велико, а р мало, то вместо формулы (8) для распределения B(n, p) используют формулу (9), где 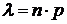 .
.
Пример 2.Радиоэлектронная система (РЭС) состоит из 200 узлов. Вероятность отказа каждого из них за время t равна 0,005. Найти 1) среднее число отказавших за время t узлов; 2) вероятность того, что за время t откажет менее 3-х узлов; 3) вероятность отказа хотя бы одного узла за время t.
Решение. Пусть СВ Х – число отказавших за время t узлов. Тогда
1) 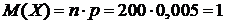 .
.
2) 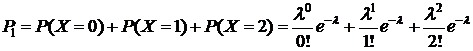 ; где
; где 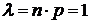 . Поэтому
. Поэтому 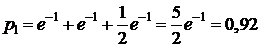 .
.
3) 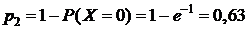 .
.
Определение 4. Непрерывная СВ Т называется распределенной по нормальному закону 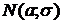 , если ее функция плотности вероятностей
, если ее функция плотности вероятностей
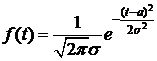 . (11)
. (11)
Замечание. 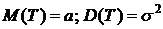 ;
;
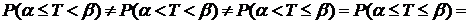
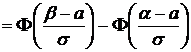 ; (12)
; (12)
где 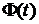 – интегральная функция Лапласа:
– интегральная функция Лапласа:
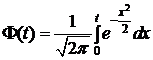 . (13)
. (13)
При этом 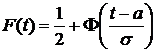 – функция распределения СВ Х.
– функция распределения СВ Х.
Если число испытаний n для СВ Х, распределенной по закону Бернулли B(n, p) велико, то используют приближенную формулу:
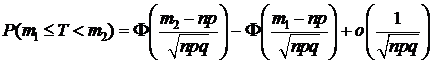 , (14)
, (14)
где р – вероятность успеха в одном испытании, 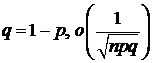 – бесконечно малая более высокого порядка малости, чем
– бесконечно малая более высокого порядка малости, чем 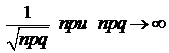 .
.
Пример 3. Пусть СВ Т задает момент времени выхода из строя производимой детали; 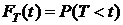 - равна вероятности того, что деталь откажет на промежутке
- равна вероятности того, что деталь откажет на промежутке 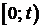 . Предположим, что Т распределена по закону
. Предположим, что Т распределена по закону 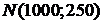 ;
; 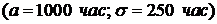 .
.
1) Найти вероятность того, что деталь проработает безотказно не менее 1250 час.
2) Вероятность того, что наработка на отказ будет находится в интервале 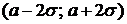 .
.
3) Вероятность того, что безотказно проработав до 1250 ч, деталь безотказно проработает и до 1750 ч.
Решение. 1) Искомая вероятность равна вероятности того, что Т примет значение из промежутка 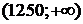 .
.
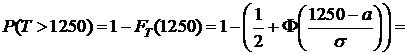
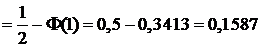 .
.
2) По формуле (12):
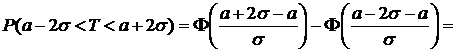
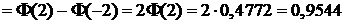 .
.
3) Необходимо вычислить условную вероятность 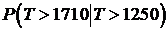 . Пусть событие А: Т > 1750, событие B: T > 1250. Тогда по формуле (2) § 1:
. Пусть событие А: Т > 1750, событие B: T > 1250. Тогда по формуле (2) § 1:
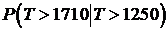 =
= 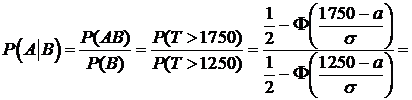
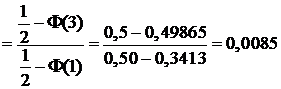 .
.
Замечание.СВ Т из примера 3 называется временем жизни или временем наработки на отказ.
Определение 5.Непрерывная СВ Х называется распределенной по экспоненциальному закону 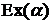 , если ее функция плотности вероятностей
, если ее функция плотности вероятностей
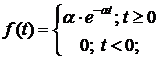 (15)
(15)
где 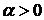 - параметр распределения.
- параметр распределения.
Замечание. 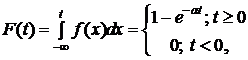 (16)
(16)
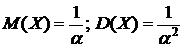 .
.
Пример 4.Время Т наработки элемента на отказ распределено по экспоненциальному закону 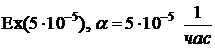 . Найти вероятность безотказной работы элемента за 500 часов.
. Найти вероятность безотказной работы элемента за 500 часов.
Решение. 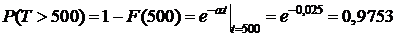 .
.
Замечание. СВ Т в примерах 3 и 4 – время жизни элемента – непрерывна. Поэтому в примерах и всюду в дальнейшем : 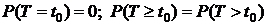 .
.
Пример 5. Вероятность безотказной работы изделия в течение 60 часов равна 0,9. Предполагается, что время жизни элемента распределено по экспоненциальному закону. Найти условную плотность вероятности того, что изделие откажет в момент времени t, при условии, что до этого изделие работало безотказно.
Решение. СВ Т – время жизни элемента; 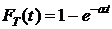 .
.
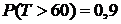 ,
, 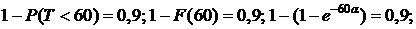
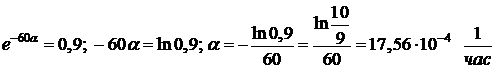 .
.
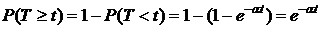 . Пусть
. Пусть 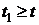 .
.
Тогда 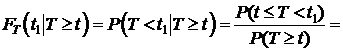
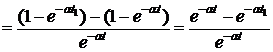 .
.
Тогда 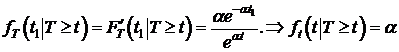 .
.
Упражнения.
2.1.Электронная система в состоянии выполнить свои задания при как min четырех исправных каналах из 5 имеющихся. Вероятность P работы каждого канала в течение времени t равна 0,8. Найти вероятность того, что
1) система будет работать;
2) система откажет.
Ответ 2.1: 1) 0,73728, 2) 0,26272.
2.2. Система имеет 4 резервных элемента. Вероятность р отказа каждого из них в течение времени t равна: р=0,25. Найти вероятность того, что в течение времени t будет исправен
1) один элемент;
2) хотя бы один элемент;
3) откажут все;
4) найти среднее число отказных элементов.
Ответ 2.2:1) 0,046875; 2) 0,9961; 3) 0,0039.
2.3. Устройство состоит из 4 независимо работающих элементов. Вероятность того, что за время t откажет хотя бы один из них равна 0,5904. Найти вероятность того, что за это время откажут:
1) 2 элемента;
2) менее 2-х;
3) не менее 2-х;
4) найти среднее число отказавших элементов.
Ответ 2.3:1) 0,1536; 2) 0,8192; 3) 0,1808; 4) 0,8.
2.4.Радиосхема состоит из 2000 узлов. Вероятность р отказа любого из них за время t равна: р=0,001. Найти вероятность того, что за время t в системе произойдет:
1) 3 отказа;
2) менее 3-х отказов;
3) не менее 3-х отказов;
4) хотя бы один отказ;
5) найти средне число отказавших элементов.
Ответ 2.4: 1) 0,180447; 2) 0,67667; 3) 0,32333; 4) 0,864665.
2.5.Время Т жизни элемента распределено по закону 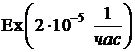 .
.
1) Написать функцию распределения 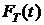 и функцию плотности вероятностей
и функцию плотности вероятностей 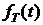 для СВ Т.
для СВ Т.
2) Определить вероятность того, что элемент будет в рабочем состоянии через а) 500 час; б) 1000 час.
3) Определить вероятность того, что время жизни лежит в промежутке 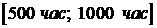 .
.
4) Определить среднее время жизни.
5) Определить вероятность того, что наработка на отказ элемента < 1000 час, при условии, что до 500 часов он работал нормально.
6) Определить какое время наработки на отказ можно гарантировать с вероятностью p=0,6.
Ответ 2.5: 2а) 0,99; 2б) 0,9801; 3) 0,00995; 4) 50000 час; 5) 0,01005; 6) 25541 час.
2.6.Время Т жизни элемента распределено по закону N (2000 час; 500 час).
1) Написать функцию распределения 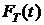 и функцию плотности вероятностей
и функцию плотности вероятностей 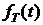 для СВ Т.
для СВ Т.
2) Определить вероятность того, что элемент будет в рабочем состоянии через а) 2000 час; б) 3000 час.
3) Определить вероятность того, что наработка на отказ лежит в промежутке 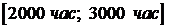 .
.
4) Определить среднее время жизни.
5) Определить вероятность того, что время жизни элемента < 3000 час, при условии, что до 2000 часов он работал нормально.
6) Определить какое время жизни можно гарантировать с вероятностью p=0,6.
Ответ 2.6: 2а) 0,5; 2б) 0,0228; 3) 0,4772; 4) 2000 час; 5) 0,9544; 6) 1875 час.
2.7. Конструкторское бюро разрабатывает прибор, рабочий ресурс которого равен a) 7000 час; b) 9000 час; c) 12000 час. При разработке можно использовать одну из четырех деталей А, В, С, D. Время наработки на отказ деталей А, В, С, D распределено соответственно по законам 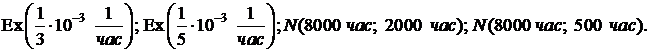 Какую из деталей предпочтительней использовать? Расположить детали в порядке убывания предпочтения.
Какую из деталей предпочтительней использовать? Расположить детали в порядке убывания предпочтения.
Ответ 2.7.а) D, C, B, A, b) C, B, A, D, c) B, C, A, D.
Основные понятия теории надежности.
Определение 1.Пусть СВ Т 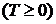 задает момент времени выхода из строя элемента (время наработки на отказ, или время жизни). Функцию распределения
задает момент времени выхода из строя элемента (время наработки на отказ, или время жизни). Функцию распределения 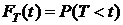 будем называть функцией ненадежности (
будем называть функцией ненадежности ( 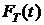 задает вероятность отказа элемента на промежутке [0 ; t)). Функцию
задает вероятность отказа элемента на промежутке [0 ; t)). Функцию
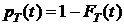 (1)
(1)
будем называть функцией надежности ( p(t) задает вероятность того, что элемент откажет на промежутке 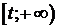 , или его время жизни
, или его время жизни 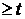 ).
).
Пример 1.Вероятность того, что изделие работало безотказно на промежутке времени [ 0; 4500) равна 0,406. Предположим, что время жизни Т распределено по экспоненциальному закону. 1) Найти Тср – среднее время жизни. 2) Найти вероятность того, что изделие будет исправно при t = Tср .
Решение. 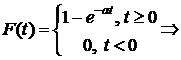 по формуле (1)
по формуле (1) 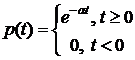 .(2)
.(2)
Тогда 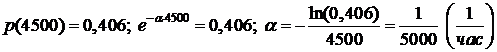 .
.
1) 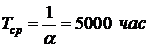 .
.
2) 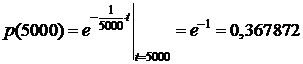 .
.
Замечание.1. Так как 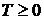 , то
, то 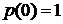 .
.
2. Так как 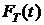 - неубывающая функция и
- неубывающая функция и 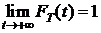 , то p(t) – невозрастающая функция и
, то p(t) – невозрастающая функция и 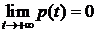 .
.
Пример 2. Пусть Т распределена по закону 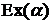 ,
,
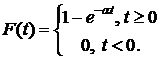 Тогда
Тогда 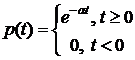 .
.
Приведем графики p(t) для 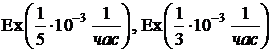 .
.
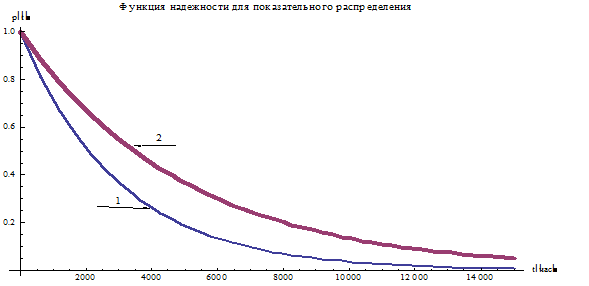
Рис. 1. Графики p(t) для экспоненциальных распределений 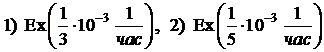 .
.
Пример 3. Пусть Т распределена по закону 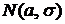 ,
,
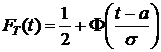 , тогда
, тогда 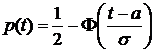 , где
, где 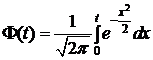 .
.
Приведем графики p(t) для N(5000 час, 1500 час) и N(5000 час, 500 час).
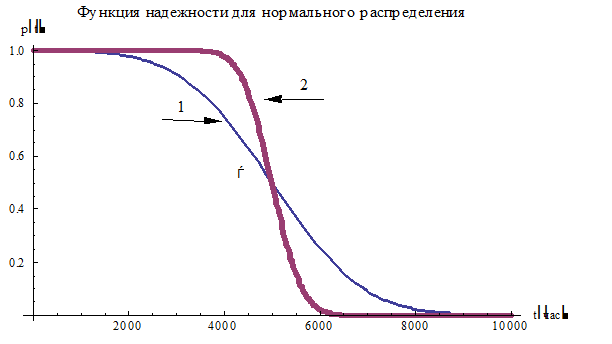
Рис 2. Графики p(t) для 1) N(5000 час, 1500 час) и 2) N(5000 час, 500 час).
Определение 2. Условная плотность вероятности отказа элемента в момент времени t, при условии, что на промежутке 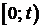 он работал безотказно, называется интенсивностью отказа элемента в момент времени t . Интенсивность отказа обозначим через
он работал безотказно, называется интенсивностью отказа элемента в момент времени t . Интенсивность отказа обозначим через 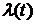 . Таким образом
. Таким образом 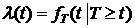 .
.
Замечание. 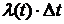 равно, при небольших
равно, при небольших 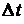 , вероятности того, что элемент, проработав безотказно на промежутке
, вероятности того, что элемент, проработав безотказно на промежутке 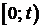 , откажет на промежутке
, откажет на промежутке 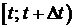 . При этом
. При этом 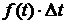 равно вероятности отказа элемента на промежутке
равно вероятности отказа элемента на промежутке 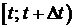 , независимо от того работоспособен он или нет в момент времени t.
, независимо от того работоспособен он или нет в момент времени t.
Теорема 1. 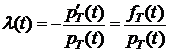 . (3)
. (3)
Доказательство. Пусть 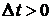 , событие А – элемент откажет на промежутке
, событие А – элемент откажет на промежутке 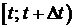 , событие В – элемент откажет на промежутке
, событие В – элемент откажет на промежутке 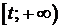 (то есть безотказно проработает на промежутке
(то есть безотказно проработает на промежутке 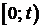 ). Тогда
). Тогда 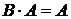 и
и
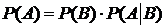 , (4)
, (4)
но 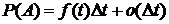 ,
, 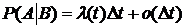 ,
, 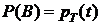 , где
, где 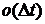 - бесконечно-малая более высокого порядка малости, чем
- бесконечно-малая более высокого порядка малости, чем 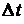 , при
, при 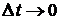 . Подставив найденные производные в формулу (4), получим
. Подставив найденные производные в формулу (4), получим
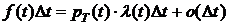
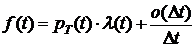 и в пределе при
и в пределе при 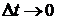 , получим
, получим 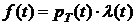 ч.т.д.
ч.т.д.
Упражнение. Доказать, что для экспоненциального распределения 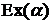 интенсивность отказов
интенсивность отказов 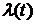 – постоянна и
– постоянна и 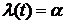 .
.
Замечание. При статистическом оценивании значений 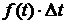 и
и 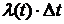 число отказавших элементов на промежутке
число отказавших элементов на промежутке 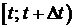 делят на число всех испытуемых ( при оценивании
делят на число всех испытуемых ( при оценивании 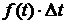 ) и на число исправных к моменту времени t (при оценивании
) и на число исправных к моменту времени t (при оценивании 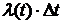 ).
).
Интенсивность отказов 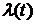 является важным показателем надежности. Его нетрудно оценить статистически и он дает наглядное представление о поведении объекта исследования. Показатель
является важным показателем надежности. Его нетрудно оценить статистически и он дает наглядное представление о поведении объекта исследования. Показатель 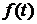 менее нагляден.
менее нагляден.
Например, рассмотрим промежуток 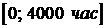 и
и 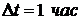 , тогда
, тогда 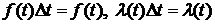 . Тогда для распределений
. Тогда для распределений 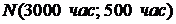 и
и 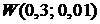 (распределение Вейбулла, см. § ) графики
(распределение Вейбулла, см. § ) графики  и
и  будут иметь вид:
будут иметь вид:
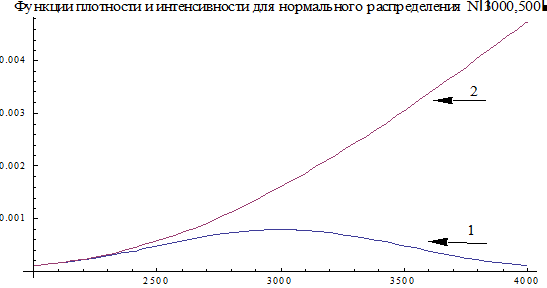
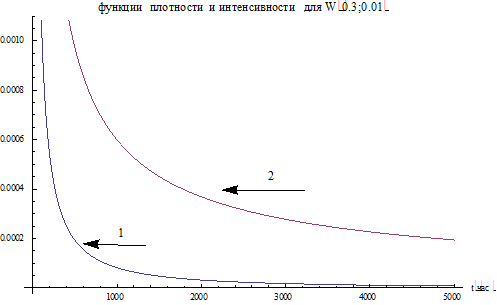
Рис.3. Графики 1) 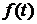 и 2)
и 2) 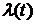 .
.
График функции 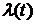 имеет во многих случаях типичную U – образную форму. Например, для системы, логическая модель надежности которой:
имеет во многих случаях типичную U – образную форму. Например, для системы, логическая модель надежности которой:
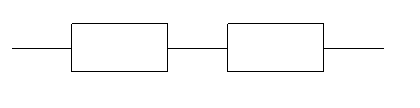
1 2 , причем
время жизни первого элемента 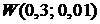 (распределение Вейбулла, см. §7, п. 7.4), а второго –
(распределение Вейбулла, см. §7, п. 7.4), а второго – 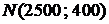 , график
, график 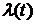 имеет вид
имеет вид
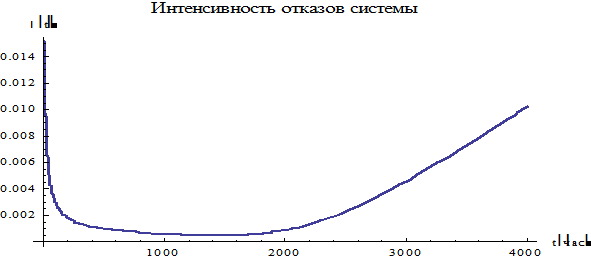
Рис.4. График функции  интенсивности отказов системы.
интенсивности отказов системы.
Замечание.Отказы на промежутке  - приработочные, отказы на промежутке
- приработочные, отказы на промежутке  вызваны старением.
вызваны старением.
Выпишем зависимости между показаниями надежности 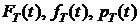 и
и 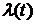 .
.
1. 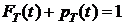 (5)
(5) 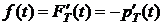 (6)
(6)
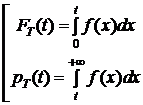 (7)
(7)
2. 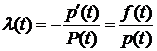 (см. теорему 1).
(см. теорему 1).
3. Выразим p(t) через 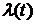 . Для этого решим дифференциальное уравнение (3), с начальными данными
. Для этого решим дифференциальное уравнение (3), с начальными данными 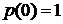 .
.
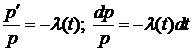
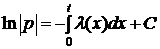
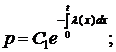 так как
так как 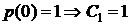 .
.
Таким образом:
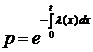 . (8)
. (8)
Найдем еще 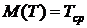 - среднее время наработки на отказ (среднее время жизни)
- среднее время наработки на отказ (среднее время жизни)
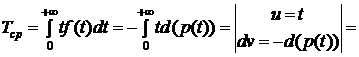
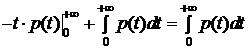 .
.
Из физических соображений считаем, что 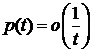 , при
, при 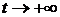 .
.
Таким образом:
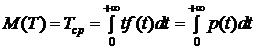 . (9)
. (9)
Аналогично 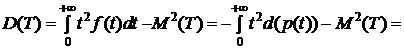
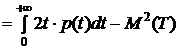 . (10)
. (10)
Упражнения.
3.1.Пусть время жизни Т элемента распределено равномерно на отрезке 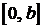 (обозначим такое распределение
(обозначим такое распределение 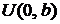 ).
).
Выписать: 1) функцию плотности вероятностей 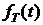 ,
,
2) функция распределения 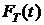 ,
,
3) функцию надежности 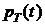 ,
,
4) функцию интенсивности отказов 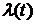 ,
,
5) среднее время жизни.
Ответ: 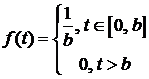 ,
,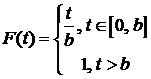 ,
,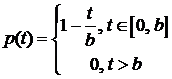 ,
,
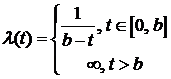 ,
,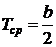 .
.
3.2.Пусть время жизни Т элемента распределено по закону:
а) 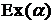 ; б)
; б) 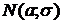 .
.
Выписать: 1) функции 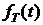 ,
, 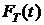 ,
,
2) функцию надежности 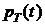 ,
,
3) функцию интенсивности отказов 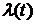 .
.
Ответ:а) 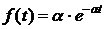 ,
, 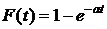 ,
, 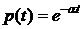 ,
, 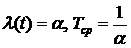 ;
;
б) 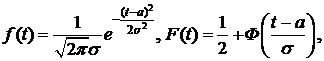
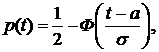
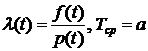 .
.
3.3.Время Т наработки элемента на отказ распределено по закону 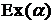 .
.
Найти вероятность того, что элемент будет в рабочем состоянии в момент времени Тср (откажет на промежутке 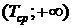 ).
).
Ответ: 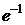 .
.
3.4.Время Т наработки элемента на отказ распределено по закону 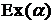 .
.
Вероятность того, что элемент работал безотказно на промежутке 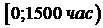 равна: p = 0,607. Найти вероятность того, что элемент будет в рабочем состоянии в момент времени t = 6000 час.
равна: p = 0,607. Найти вероятность того, что элемент будет в рабочем состоянии в момент времени t = 6000 час.
Ответ: 0,1358.
3.5.Время Т наработки элемента на отказ распределено по закону 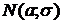 . Вероятность того, что элемент в рабочем состоянии в момент времени
. Вероятность того, что элемент в рабочем состоянии в момент времени  . Та же вероятность для момента времени
. Та же вероятность для момента времени 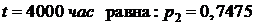 . Найти вероятность того, что элемент будет в рабочем состоянии в момент времени а) t=5000 час, б) t=7000 час.
. Найти вероятность того, что элемент будет в рабочем состоянии в момент времени а) t=5000 час, б) t=7000 час.
Ответ:а) 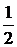 ; б) 0,09.
; б) 0,09.
Упражнения.
4.1.На испытаниях находилось 100 элементов в течение а) 500 час, б) 400 часов. Данные об отказах собраны в таблице.
Найти 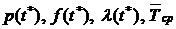 .
.
а)
| Интервалы времени (час) | 0 - 100 | 100 - 200 | 200 - 300 | 300 - 400 | 400 - 500 |
| Число отказавших элементов |
Ответ: а)
| Интервалы времени (час) | 0 - 100 | 100 - 200 | 200 - 300 | 300 - 400 | 400 - 500 |
| Число отказавших элементов | |||||
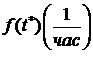 | 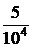 | 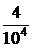 | 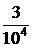 | 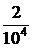 | 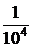 |
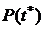 | 0,95 | 0,91 | 0,88 | 0,86 | 0,85 |
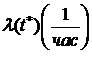 | 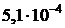 | 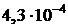 | 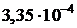 | 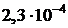 | 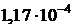 |
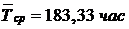 .
.
б)
| Интервалы времени (час) | 0 - 80 | 80 - 160 | 160 - 240 | 240 - 320 | 320 - 400 |
| Число отказавших элементов |
Ответ:б)
| Интервалы времени (час) | 0 - 80 | 80 - 160 | 160 - 240 | 240 - 320 | 320 - 400 |
| Число отказавших элементов | |||||
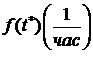 | 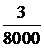 | 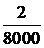 | 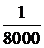 | 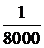 | 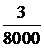 |
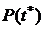 | 0,97 | 0,95 | 0,94 | 0,93 | 0,9 |
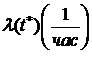 | 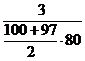 | 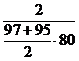 | 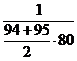 | 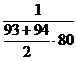 | 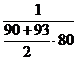 |
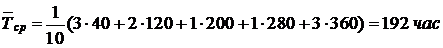 .
.
4.2. Из 4000 СВЧ диодов за месяц испытаний перегорело 5 диодов, а через полгода из оставшихся 3970 диодов за месяц перегорело 3. Определить, когда диод работает более надежно.
Ответ:через полгода.
Пример 1.
| Тип резервирования | Логическая схема | Комментарий | |
| Общее резервирование, постоянно включенный резерв | 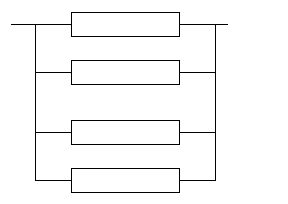 0 Осн. устр. 0 Осн. устр. | Целая кратность 3 | |
| Резервирование замещением | 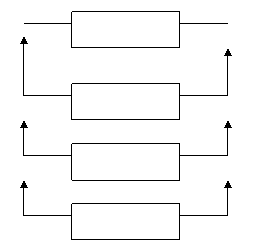 Осн. устр. Осн. устр. | Целая кратность 3 | |
| Поэлементное, с постоянным резервом | 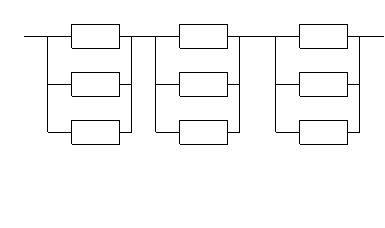 1 2 3 0 0 0 1 1 1 2 2 2 1 2 3 0 0 0 1 1 1 2 2 2 | Целая кратность 2 | |
| Поэлементное, замещением | 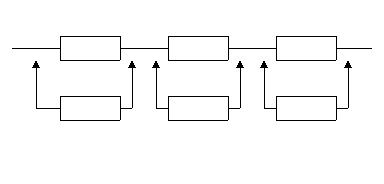 0 0 0 1 1 1 0 0 0 1 1 1 | Целая кратность 1 | |
| Тип резервирования | Логическая схема | Комментарий | |
| Поэлементное, с постоянным резервом |  01 02 11 12 01 02 11 12 | Для элемента 01 – целая кратность 2, для элемента 02 – целая кратность 1 | |
| Поэлементное, с постоянным резервом | 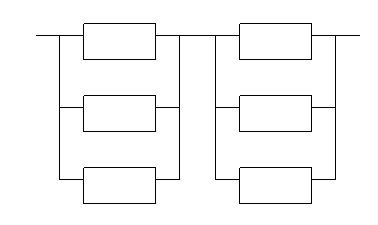 0 0 0 0 1 1 0 0 0 0 1 1 | Дробная кратность 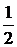 | |
