Воспользуемся совместным законом распределения, полученным в задаче 1.

, , ,

, , ,

, , ,

, , .

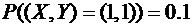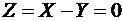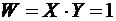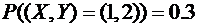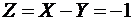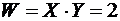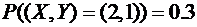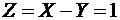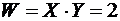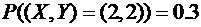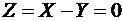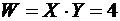Таким образом ,

а) случайная величина 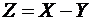принимает значения -1, 0, 1 со следующими вероятностями

,

,

.

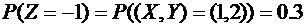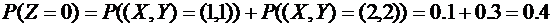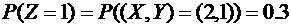Запишем это распределение в виде таблицы

Z	-1
P	0.3	0.4	0.3

б) Случайная величина 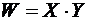принимает значения 1, 2, 4 со следующими вероятностями

,

,

.

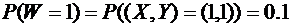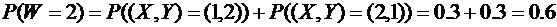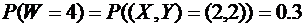Запишем это распределение в виде таблицы

W
P	0.1	0.6	0.3

◄

Функция

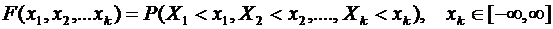
называется совместной функцией распределения величин .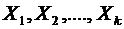

◄▬▬▬■

3. Числовые характеристики случайных величин. В ряде задач не требуется полностью знать поведение случайной величины, для решения достаточно лишь нескольких характеристик. Одной из основных числовых характеристик является математическое ожидание (или взвешенное среднее значение), представляющее собой среднее значение рассматриваемой случайной величины с учетом вероятностей принимаемых значений и вычисляемое по формуле:

.

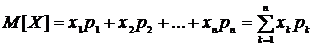Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений на их вероятности. Для бесконечной случайной величины: .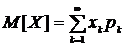

Математическое ожидание случайной величины Х называется центром распределения вероятностей случайной величины.

Свойства математического ожидания.

1) Линейность: для любых постоянных 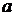и

;

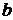
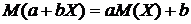2) аддитивность: для любых случайных величин 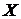и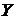

;

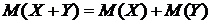3) для независимых случайных величин 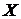и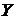

;

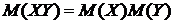4) если 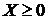, то 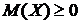, если 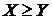, то .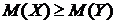

Кроме того, зная математическое ожидание случайной величины, полезно знать и диапазон ее возможного отклонения от этого значения. Другими словами, если значения случайной величины в основном ненамного отклоняются от среднего, то оно хорошо характеризует исследуемую величину; в противном случае знание математического ожидания мало что дает для описания ее поведения. Характеристикой, показывающей масштаб отклонения случайной величины от математического ожидания, является дисперсия — математическое ожидание квадрата отклонения от среднего:

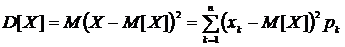
Смысл дисперсии заключается в том, что она характеризует средний квадратичный разброс случайной величины вокруг своего математического ожидания.

Замечание. Если 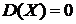, то в силу определения дисперсии , т.е. фактически 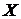– детерминированная ( не случайная ) величина.

Свойства дисперсии.

1. Для любой случайной величины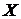

;

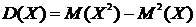2. D[C]=0, где С=const.

3. D[CX]=C²·D[X].

4. Для независимых случайных величин Х и У D[X+Y]= D[X] + D[Y].

В частности, из свойств дисперсии следует, что

D[С+Х]= D[X]

D[X - Y]= D[X] + D[Y].

Отклонение случайной величины от математического ожидания задается средним квадратическим отклонением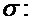

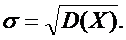
Пример. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины 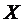из предыдущего примера.

Используя найденный ряд распределения, получим:

◄

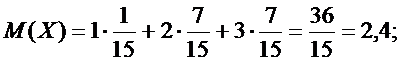
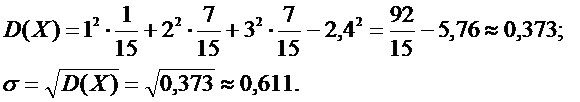Примеры.

1.Случайная величина Х задана следующим законом распределения:

Х
Р	0,3	0,4	0,3