Классическое определение вероятности. Относительная

КЛАССИЧЕСКАЯ ТЕОРИЯ

ВЕРОЯТНОСТЕЙ

1. СЛУЧАЙНЫЕ СОБЫТИЯ

1.1. Некоторые формулы комбинаторики

Правило произведения. Если объект А может быть выбран n₁ способами и после каждого такого выбора объект В может быть выбран n₂ способами, то выбор пары А и В может быть осуществлен n₁ 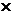n₂ способами. Это правило распространяется и на случай выбора трёх, четырёх и т.д. объектов.

Правило суммы. Если первое событие может произойти n₁ способами, а второе - n₂ способами независимо от первого, то первое или второе события могут произойти n₁+n₂ способами.

Рассмотрим некоторое множество Х, состоящее из n элементов 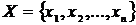. Будем выбирать из этого множества различные упорядоченные подмножества У из k элементов. Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор 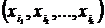элементов множества Х.

Если выбор элементов множества У из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле n^k.

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается 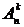и определяется равенством .

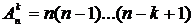Пример. Пусть даны пять цифр: 1; 2; 3; 4; 5. Определим сколько трехзначных чисел можно составить из этих цифр. Если цифры могут повторяться, то количество трехзначных чисел будет 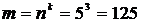. Если цифры не повторяются, то . ◄

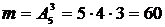Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно .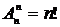

Пусть теперь из множества Х выбирается неупорядоченное подмножество У, т.е. два подмножества У₁ и У₂ из k элементов, состоящие из одних и тех же элементов и отличающиеся их порядком будем считать одинаковыми. Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается 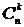и равно

.

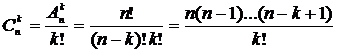В дальнейшем будем считать 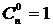. Заметим, что справедливо равенство .

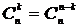Пример. В группе из 27 человек нужно выбрать трех делегатов на профсоюзную конференцию. Найдем сколькими способами это можно сделать

. ◄

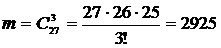Классическое определение вероятности. Относительная

Частота события. Статистическое определение

Примеры.

1. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?

Пусть событие А – номер вынутого шара не превосходит 10. Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. ◄

2. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. ◄

3. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?

Здесь всего случаев n=36. Событие А – появление карты пиковой масти. Число случаев, благоприятствующих появлению события А, m=9. Следовательно, . ◄

4. Бросаются одновременно две монеты. Какова вероятность выпадения герба на обеих монетах?

Составим схему возможных случаев.

	Первая монета	Вторая монета
1 случай 2 случай 3 случай 4 случай	герб герб не герб не герб	герб не герб герб не герб

Всего случаев 4. Благоприятствующих случаев 1. Следовательно, р=1/4. ◄

5. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?

Вынуть два шара из десяти можно следующим числом способов: . Число случаев, когда среди этих двух шаров будут оба белые, равно . Искомая вероятность будет . ◄

6. Из коробки, в которой лежат пять пирожных «эклер» и семь — «наполеон», достали пять пирожных. Найти вероятность того, что среди них два «эклера» и три «наполеона».

Количество возможных исходов опыта представляет собой число сочетаний из 12 по 5:

Число благоприятных исходов является произведением количества способов, которыми можно выбрать два «эклера» из пяти имеющихся, и числа наборов по три «наполеона» из семи:

Следовательно, искомая вероятность равна ◄

7. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.

Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е. . ◄

Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать способами. Следовательно, число благоприятствующих исходов равно .

Искомая вероятность . ◄

8. Пять книг расставляются на полку. Найти вероятность того, что две определенные книги окажутся рядом.

Число всех способов, которыми можно расставить на полке пять книг, равно числу перестановок из пяти элементов .

Подсчитаем число благоприятствующих случаев. Две определенные книги можно поставить рядом 2!=2 способами. Оставшиеся книги можно расположить на полке способами. Поэтому .

Итак, . ◄

2. Статистическое определение вероятности.Недостатком классического определения вероятности является то, что не всегда удается узнать, являются исходы испытания равновозможными или не являются.

Относительной частотойр^* случайного события А называется отношение числа m^* появления данного события к общему числу n^* проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться данное событие.

.

Оказывается, что при большом числе испытаний n, относительная частота появления события А в различных сериях отличается друг от друга мало и это отличие тем меньше, чем больше испытаний в сериях.

При статистическом определении вероятностью события называют относительную частоту события при большом числе испытаний или число близкое к ней:

.

3. Геометрический метод вычисления вероятностей.Если множество возможных исходов опыта можно представить в виде отрезка прямой или в виде некоторой плоской или трехмерной области, а множество исходов, благоприятных событию — как часть этой области, то вероятность рассматриваемого события определяется следующим образом:

где — длина отрезка (площадь или объем области), задающего множество возможных исходов, а — соответствующая мера множества благоприятных исходов.

Пример.В круг наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг.

В этом случае мерой множества возможных исходов является площадь круга: а мерой множества благоприятных исходов — разность площадей круга и треугольника: . Следовательно, вероятность заданного события равна

◄

Вопросы для самопроверки

1. Что понимается под событием? Как подразделяются события?

2. Какие события называются элементарными или случаями?

3. Сформулируйте аксиомы теории вероятностей и следствия из них

4. Сформулируйте классическое определение вероятности события. Укажите возможные границы вероятности.

5. Что такое относительная частота появления события или частость? В чем состоит свойство статистической устойчивости относительной частоты? В чем состоит различие между вероятностью и относительной частотой?

Теоремы сложения и

Умножения вероятностей

Теоремы сложения и умножения вероятностей являются основными, так как на них основываются все дальнейшие положения теории вероятностей. Указанные теоремы позволяют по вероятностям одних событий вычислять вероятности других. В следствии этого они часто применяются для решения различных задач. Следует усвоить методику использования теорем при решении задач.

Суммой событий и называется событие, заключающееся в том, что произошло хотя бы одно из событий и , а произведением этих событий — событие, состоящее в том, что произошли оба данных события.

Вероятность суммы двух событий можно найти по теореме сложения вероятностей:

Если события и несовместны, то есть не могут произойти одновременно, то вероятность их произведения равна нулю, и теорема сложения приобретает более простой вид:

Вероятность произведения событий определяется по теореме умножения вероятностей:

где — так называемая условная вероятность события , то есть вероятность при условии, что произошло. Если осуществление события не изменяет вероятности события , то и называются независимыми, и вероятность их произведения равна произведению вероятностей сомножителей:

Заметим, что при решении задач теоремы сложения и умножения обычно используются совместно.

Примеры.

1.В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар а) синий или черный; б) белый, черный или синий.

Обозначим следующие события:

Б – вынули белый шар, ;

Ч – вынули черный шар, ;

С – вынули синий шар, ;

К – вынули красный шар, .

Тогда искомые вероятности будут:

а) .

б)

или . ◄

2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Рассмотрим два способа решения задачи.

Первый способ. Пусть события А – хотя бы один учебник в переплете;

В – один из взятых учебников в переплете, два – без переплета;

С – два в переплете, один без переплета;

D – все три учебника в переплете.

Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.

, , .

Тогда

.

Второй способ. Вновь А – хотя бы один учебник в переплете;

- ни один из взятых учебников не имеет переплета.

Так как события А и противоположные, то

. ◄

3. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания равны соответственно 0,6 и 0,9. Найти вероятности следующих событий:

— оба попали в цель;

— в цель попал хотя бы один.

Назовем событиями и попадание в мишень соответственно первого и второго стрелка и отметим, что и являются событиями совместными, но независимыми (иными словами, в мишень могут попасть оба стрелка, а вероятность попадания каждого не зависит от результата другого). Событие представляет собой произведение событий и поэтому

Событие является суммой и для определения его вероятности воспользуемся общим видом теоремы сложения:

◄

4. В первом ящике 2 белых и 7 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Обозначим события: А – вынули белый шар из первого ящика, ;

- вынули черный шар из первого ящика, ;

В – белый шар из второго ящика, ;

- черный шар из второго ящика, .

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей , . Тогда искомая вероятность по теореме сложения будет

. ◄

5. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха; в) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, Р(А)=0,8; В – попадание второго стрелка, Р(В)=0,9. Тогда - промах первого, ; - промах второго, . Найдем нужные вероятности.

а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.

б) - двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) - одно попадание,

. ◄

6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.

2. .

3. P(АВС)=0,6·0,7·0,8=0,336. ◄

7.Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.

а) Обозначим события А – среди взятых 6 деталей нестандартных нет;

В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6 деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что

,

.

Откуда

.

б) Пусть теперь событие А – в шести взятых деталях не более двух нестандартных. Тогда - в выбранных деталях более двух нестандартных, т.е. три.

.

. ◄

8. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?

1-й способ. Рассмотрим события: - появление шестерки на первой кости ( ); - появление шестерки на второй кости ( ). События и - совместны и независимы, следовательно,

.

2-й способ. Рассмотрим противоположные события: и . Из свойств вероятности и алгебры событий следует

.

Следовательно,

. ◄

9.В классе 32 ученика.12 из них носят очки. У 10 – пятерка по русскому языку, из них пятеро носит очки. Определить зависит ли между собой события: ученик носит очки и у ученика пятерка по поведению.

Пусть событие ={ученик носит очки}, событие ={у ученика пятерка по русскому языку}.

Тогда .

Так как , то эти события не независимы. ◄

Формула полной вероятности

И формула Байеса

1. Если событие может произойти одновременно с одним из событий , представляющих собой так называемую полную группу попарно несовместных событий (то есть в результате опыта обязательно произойдет одно и только одно событие из этой группы), то события называются гипотезами, а вероятность события определяется по формуле полной вероятности:

Здесь — вероятность -ой гипотезы, а — условная вероятность события при осуществлении данной гипотезы.

Примеры.

1.В трех одинаковых урнах лежат шары: в первой — 5 белых и 3 черных, во второй — 2 белых и 6 черных, в третьей — 3 белых и 1 черный. Из случайно выбранной урны вынут шар. Найти вероятность того, что он белый.

Будем считать гипотезами выбор одной из урн. Поскольку урны одинаковы, каждую из них можно выбрать с одинаковой вероятностью, а так как сумма вероятностей гипотез равна 1, то вероятность каждой гипотезы —

Условная вероятность события , то есть извлечения белого шара из урны, определяется по классическому определению вероятности (количеством благоприятных исходов при этом является число белых шаров, а числом возможных исходов — общее число шаров в урне). Поэтому

Используя формулу полной вероятности, получаем:

◄

2. Вероятность изготовления годного изделия данным станком 0,9. Вероятность появления изделия первого сорта среди годных изделий 0,8. Определить вероятность изготовления изделия первого сорта данным станком.

Событие В – изготовление годного изделия данным станком; событие А – появление изделия первого сорта. Очевидно, Р(В)=0,9, . Искомая вероятность будет

. ◄

3. К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса билета?

Пусть события: А – студент знает первый вопрос;

В – студент знает второй вопрос;

С – студент знает третий вопрос.

Примеры.

1. В студенческой группе 20 студентов. Из них 5 отличников, которые знают все экзаменационные вопросы, 8 студентов знают ответы на 70 % вопросов и 7 — на 50 %. Первый вызванный студент ответил на первый вопрос экзаменационного билета. Найти вероятность того, что он отличник.

Будем считать гипотезой то, что данный студент является отличником, — что он принадлежит ко второй группе, — к третьей. Тогда вероятности гипотез равны:

Найдем условную вероятность события — правильного ответа на первый вопрос — при осуществлении каждой гипотезы:

Следовательно, полная вероятность события равна

Применяя формулу Байеса, находим:

◄

2.30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.

Событие А – безотказная работа прибора;

В₁ – прибор собран специалистом высокой квалификации;

В₂ – прибор собран специалистом средней квалификации.

Выпишем вероятности гипотез: , .

Условные вероятности события А: , .

Вероятность события А: . Определим вероятность гипотезы В₁ при условии, что событие А произошло

.◄

3.Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие попало, если вероятности попадания в цель каждым из орудий равны р₁=0,4, р₂=0,3, р₃=0,5.

Обозначим события: А – два орудия попали в цель;

В₁ – первое орудие попало в цель;

В₂ – первое орудие не попало в цель.

Вероятности гипотез: , .

Условные вероятности события А:

.

.

По формуле Байеса

. ◄

Вопросы для самопроверки

1. Что понимается под суммой двух событий?

2. Сформулируйте теорему сложения вероятностей для несовместных событий?

3. Что понимается под полной группой событий? Чему равна сумма вероятностей несовместных событий, составляющих полную группу?

4. Какие события называются противоположными? Чему равна сумма вероятностей противоположных событий?

5. Дайте определение условной вероятности. Какие события называются независимыми?

6. Что понимается под произведением двух событий?

7. Сформулируйте теорему умножения вероятностей для независимых и зависимых событий.

8. Докажите формулу полной вероятности.

9. Докажите формулу Байеса.

Повторные независимые

Испытания

В теме изучаются методы решения задачи, в которой один и тот же опыт повторяется несколько раз. В результате каждого опыта может появиться или не появиться интересующее нас событие. Однако нас интересует не результат отдельного опыта, а результат серии опытов, т. е. какова вероятность появления того или иного числа событий в серии опытов. Характерным примером такой задачи являются различного рода выборки. Когда образована выборка и произ­водится ее изучение, то каждый элемент ее обследуется и устанавливается на­личие или отсутствие того или иного фактора. Обследование одного элемента выборки и есть опыт или испытание. Обследование всех элементов выборки, про­водимое в одинаковых условиях, есть повторение испытаний, рассматриваемое в задаче о повторении опытов.

Формула Пуассона наряду с задачей повторения испытаний используется также для расчета вероятности появления различного числа событий (например, точек или других элементов) в какой-либо области (площади, объеме или во времени). При этом должны соблюдаться следующие условия: события (точки) в области распределены в общем равномерно;положение каждого события (точки) случайное, независимое друг от друга;события (точки) появляются в области поодиночке, а не парами, тройками и т. д.

При решении задач с использова­нием формулы Пуассона исходные данные могут встречаться в двух вариантах:

1) в условии задачи указывается вероятность р появления события в одном испытании и число испытаний n;

2) в условии задачи указывается среднее число появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события.

В первом случае параметр распределения Пуассона определяется как про­изведение вероятности р и числа п испытаний: = пр.

Во втором случае этот параметр определяется произведением среднего чис­ла появлений события и размера области: .

Дальнейший расчет вероятности по формуле Пуассона одинаков в обоих случаях.

1. Формула Бернулли.Рассмотрим случай, когда требуется определить не вероятность осуществления некоторого события в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из опытов. Будем считать при этом, что вероятность в каждом опыте одинакова и результат каждого опыта не зависит от результатов остальных. Такая постановка задачи называется схемой независимых испытаний. При выполнении указанных условий вероятность того, что при проведении независимых испытаний событие будет наблюдаться ровно раз (неважно, в каких именно опытах), определяется по формуле Бернулли:

где — вероятность появления в каждом испытании, а — вероятность того, что в данном опыте событие не произошло.

В частности, отсюда Р_n(0)=qⁿ, Р_n(1)=npq^n-1, … , Р_n(n)=pⁿ.

Примеры.

1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Событие А – достали белый шар. Тогда вероятности , . По формуле Бернулли требуемая вероятность

. ◄

2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Вероятность рождения девочки , тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность

. ◄

3. Правильная игральная кость бросается четыре раза. Найти вероятность того, что шесть очков выпадут ровно два раза.

Обозначим {выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с , , а так как кость правильная . Вычислим

.

Подставляя эти значения в формулу Бернулли, получим искомую вероятность

. ◄

4.Вероятность появления события в каждом из 5 независимых испытаний равна 0.8 . Найти вероятность того, что событие А произойдет

а) не менее трех раз б) не более двух раз.

Имеем ,

Подставляя эти значения в формулу для , получим

а)

.

б)

Нетрудно видеть, что событие а) = { не менее двух попаданий при шести выстрелах, т.е. 2, 3, 4, 5, 6 попаданий} и событие б) ={не более одного попадания при шести выстрелах, т.е. 0 и 1 попадание } составляют полную группу событий с суммой вероятностей равной 1, . Поэтому вероятность события б) можно подсчитать, используя значение , полученное в а) . ◄

■▬▬▬►

2. Число наступлений события называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления любое другое количество раз.

Наивероятнейшее число наступлений события в испытаниях заключено между числами и .

Замечание. Если – целое число, то наивероятнейших чисел два: и .

Пример. Вероятность попадания в цель при каждом выстреле из лука равна 1/3. Производится шесть выстрелов. Какова вероятность ровно двух попаданий? Какова вероятность не менее двух попаданий? Каково наивероятнейшее число попаданий?

Обозначим A = {попадание при одном выстреле} p = 1/3, q = 1 – 1/3 = 2/3. Число выстрелов n = 6. Естественно предположить, что выстрелы не зависят друг от друга, и мы имеем схему Бернулли.

Ответ на первый вопрос находим по формуле Бернулли, n = 4, m =2

.

Ответ на второй вопрос можно найти по формуле для . Однако проще найти по этой формуле, вероятность не более одного попадания и вычесть эту вероятность из 1.

.

В этом рассуждении мы использовали тот факт, что событие B₁ = { не менее дву