Свойства условных вероятностей

Операции над событиями.

Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

Определение. Объединениемили суммой событий А_k называется событие A, которое означает появление хотя бы одногоиз событий А_k.

Определение. Пересечениемили произведениемсобытий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

Определение. Дополнительным к событию А называется событие , означающее, что событие Ане происходит.

Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

4) Свойства операций над событиями:

1. А+В=В+А, АВ=ВА – переместительное свойство

2. (А+В)?С=А?С+В?С, А?С+В=(А+В) ?(А+С) – распределительное свойство

3. (А+В)+С = А+(В+С), (АВ) ?С=А?(ВС) – сочетательное свойство

4. А+А=А, А?А=А

5. А+?=?, А?? = А

6. = ?, ?

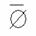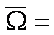7. А-В=А?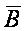

8. 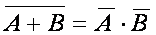, 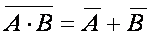- законы де Моргана.

5. Статистическое определение вероятности события, ее свойства.

Рассмотрим некоторый стахастический эксперимент и событие А, наблюдаемое в этом экс-те. Предположим, что проводится серия n-независимых испытаний этого типа. Относительной частотой события А называется отношение числа экспериментов, в которых событие А произошло к общему числу проведенных экспериментов: 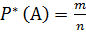, где m- число эксп-ов, в которых событие А произошло; n- общее число эксп-ов.Свойства: 1. Число исходов конечное; 2. Приблизительное значение.

6.Классическое определение вероятности, ее свойства.

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия.

С в о й с т в о 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,

Р (A) = m / n = n / n = 1.

С в о й с т в о 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

Р (А) = m / n = 0 / n = 0.

С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m / n < 1, следовательно,

0 <Р (А) < 1

7. Геометрическое определение вероятности.Предположим, что на отрезок длины 4 на удачу бросают точку. Вероятность попадания точки в любую часть отрезка пропорциональна длине этой части отрезка и не зависит от её месторасположения.

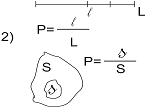
Вероятность не зависит от месторасположения и термин участка S.

3)Для объема : р=v/V

8. Аксиоматическое определение вероятности.Вероятностью наз-сячисловая ф-ция, определенная на поле событий S и обладающая след. Действиями: Аксиома 1.Для любого события А принадлежит S. Р(А)>=0. Аксиома 2.Вероятность достоверного события =1.Аксиома 3.Вероятность объединения двух несовместных соб-й равна сумме вер-й этих соб-й.А*В=0, Р(А+В)=Р(А)+Р(В).

9. Теорема сложения вероятностей и следствия из нее. Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Определение. Противоположными называются два несовместных события, образующие полную группу. Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Следствие 2: Сумма вероятностей противоположных событий равна единице.

10. Условная вероятность, ее свойства.Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. Пусть (амегабольшая, F, P) - фиксированное вероятностное пространство. Пусть А, В принадлежит F суть два случайных события, причём Р(В)>0 . Тогда условной вероятностью события А при условии события В наз-я Р(А|B)=P(A∩В)/P(B)

Математическая формулировка

,

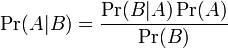где

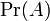— априорная вероятность гипотезы A;

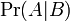— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

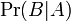— вероятность наступления события B при истинности гипотезы A;

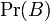— вероятность наступления события B.

20.

Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях собы­тие А состоится число раз, заключенное в границах от а до b включительно (а <b), приближенно равна: 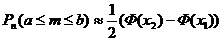,где функция Ф (х) определяется равенством 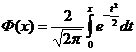, 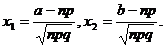свойства функции Ф(х).Функция Ф(х) нечетная, т. е. Ф (—х) = — Ф(х). Функция Ф(х) монотонно возрастающая. Предел функции Ф(х) при 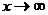равен единице. Для всех значений х > 5 можно считать, что 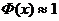. Уже Ф (5) = 0,99999994, а тем более Ф (х) » 1, если х > 5, так как при увеличении х функция Ф (х) возрастает, но не может пре­восходить. Поэтому в таблицах функция дана для значений х > 5.

23.

24.

Определение.Плотностьюраспределениявероятностейнепрерывнойслучайнойвеличины 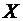называетсяфункцияf(x) – перваяпроизводная от функциираспределения 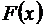. 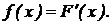Свойстваплотностираспределения

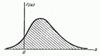1. Плотностьраспределения – неотрицательнаяфункция. 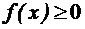2. Несобственныйинтеграл от плотностираспределения в пределах от - ¥ до ¥равенединице. 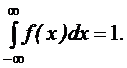Криваяраспределениявероятностей - кривая, характеризующаяраспределениевероятностейпоявлениявеличиныгидрологическогоэлемента.Кривая, изображающаяплотностьраспределенияслучайнойвеличины, называетсякривойраспределения

Рассматривая плотность распределения 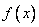для одной случайной величины, мы ввели понятие «элемента вероятности» 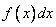. Это есть вероятность попадания случайной величины 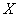на элементарный участок 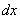, прилегающий к точке 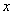. Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение 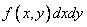.Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами 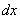, , 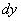примыкающий к точке

25. Дискретнаяс.в. – это с.в., принимающая конечное или счетное число значений.1).Мат. Ожидание: Свойства: Mc=c, c=const; Mcx=cMx; M(x+y)=M(x)+M(y);M(xy)=MxMy;

2).Дисперсия-среднее значение квадрата отклонения с.в. от ее среднего значения.Dx=Mx²–(Mx)². Свойства: Dc=o, c=const; Dcx=c²Dx; D(x+y)=Dx + Dy; 3). Среднее квадр. Отклонение – 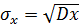. 4).Модой с.в. х наз. число М₀, которое равно её наиболее вероятному значению. ; 5).Медианой с.в. наз. такое число, что:

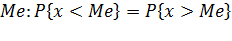
27Мода и медиана с.в.

Модад.с.в. – это наиболее вероятное значение с.в.; для н.с.в. – это точка максимума плотности распределения. Обозначение: Мo_х.

МедианаМe_х с.в. - это такое значение с.в., для которого P{X<xm}=P{X>xm}=1/2

Медиана является характеристикой н.с.в..

Геометрически медиана- это точка на оси 0x для которой площади под графиком плотности распределения, лежащие слева и справа от нее, одинаковы и равны 21.

Если плотность распределения симметрична относительно прямой x=a и распределение одномодально, то математическое ожидание, медиана и мода совпадают между собой,

M(X)=Mex=MОx

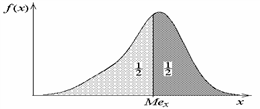
28Свойства математического ожидания и дисперсии случайной величины.

свойствадисперсиии.
1. D(X)≥0

2. D(c)=0

3. D(cX)=c2D(X)

4D(X+Y)=D(X)+D(Y) где(Х,Y - независимые с.в.)

5D(X+с)= D(X)

1) Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

Свойства мат ожидания

M[C] = C.

M[CX] = CM[X].

M[XY ] = M[X]M[Y ].

M[X + Y ] = M[X] +M[Y ]

M[X] = np( произведение числа ожиданий на вероятность)

29. Начальные и центральные моменты дискретной с.в. Коэффициент асимметрии, эксцесс.

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a k = Mx k.

Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx )k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a 1 = Mx , а дисперсия - центральный момент второго порядка,

a 2 = Mx 2 = M(x - Mx )2 = Dx .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

m 2=a 2-a 12, m 3 = a 3 - 3a 2a 1 + 2a 13.

Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.

В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой ,

где m 3 - центральный момент третьего порядка, - среднеквадратичное отклонение.

Эксцесс Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x , от нормального распределения, является эксцесс.

Эксцесс g случайной величины x определяется равенством .

У нормального распределения, естественно, g = 0. Если g (x )> 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x ) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.

30.Бернуллиевскаяс.в., ее математическое ожидание и дисперсия.

Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность 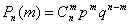, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
Мх=npDx=npqq=1-p

31Пуассоновская с.в., ее математическое ожидание и дисперсия.

Случайная величина имеет распределение Пуассона с параметром альфа (альфа > 0), если

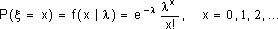
Что кратко записывается в виде L(кси) = П(кси); при этом альфа= Мх = Dх.

Альфа = np

Закон распределения называется равномерным, если

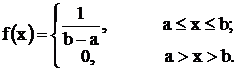
ф-цияраспред.: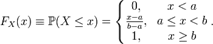

,

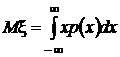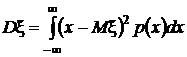
Случайная величина распределена по показательному закону, если

;

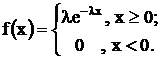
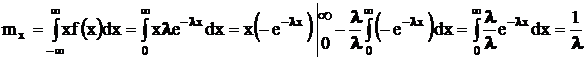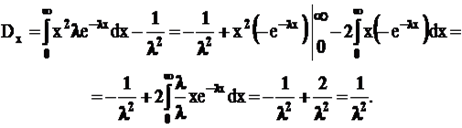
36. Случайная величина распределена по нормальному закону распределения, если 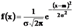; 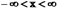.Нормально распределенная случайная величина X имеет математическое ожидание, равное нулюДисперсия определяет форму кривой нормального закона распределения.

Чаще всего используют нормальный закон в нормированной форме , который получают заменой переменной . .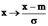

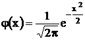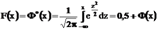; для ; .

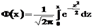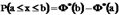37.Известно, что если случайная величина X задана плотностью распределения 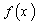, то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова: .

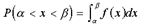Пусть случайная величина X распределена по нормальному закону. Тогда .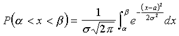

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную 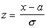. Отсюда .

Найдем новые пределы интегрирования. Если 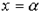, то 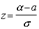, если 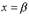, то 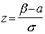. Тогда

.

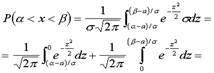
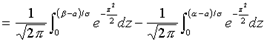Выражение 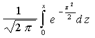, входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:

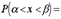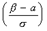Ф — Ф ,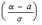

где Ф(x) = .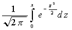

Эту формулу называют формулой Лапласа.

Если случайная величина X является признаком генеральной совокупности, то формула Лапласа дает долю элементов генеральной совокупности, у которых значение признака X находится в границах от 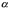до .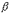

Интеграл, через который выражается функция Лапласа, нельзя выразить через элементарные функции. Его можно представить в виде степенного ряда, если разложить в ряд подынтегральную функцию 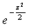и почленно проинтегрировать ряд. Тогда

Ф(x) = .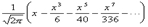

C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.

Отметим ряд свойств функции Лапласа, полезных для применения.

1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).

2. Функция Ф(x) – возрастающая, быстро приближающаяся к своему пределу, равному 0,5: Ф(0) = 0, Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986, Ф(4) = 0,4999 и т.д. На практике полагают Ф(x) 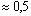для x>5.

Операции над событиями.

Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

Определение. Объединениемили суммой событий А_k называется событие A, которое означает появление хотя бы одногоиз событий А_k.

Определение. Пересечениемили произведениемсобытий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

Определение. Дополнительным к событию А называется событие , означающее, что событие Ане происходит.

Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

4) Свойства операций над событиями:

1. А+В=В+А, АВ=ВА – переместительное свойство

2. (А+В)?С=А?С+В?С, А?С+В=(А+В) ?(А+С) – распределительное свойство

3. (А+В)+С = А+(В+С), (АВ) ?С=А?(ВС) – сочетательное свойство

4. А+А=А, А?А=А

5. А+?=?, А?? = А

6. = ?, ?

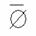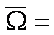7. А-В=А?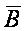

8. 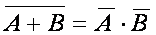, 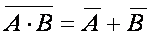- законы де Моргана.

5. Статистическое определение вероятности события, ее свойства.

Рассмотрим некоторый стахастический эксперимент и событие А, наблюдаемое в этом экс-те. Предположим, что проводится серия n-независимых испытаний этого типа. Относительной частотой события А называется отношение числа экспериментов, в которых событие А произошло к общему числу проведенных экспериментов: 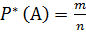, где m- число эксп-ов, в которых событие А произошло; n- общее число эксп-ов.Свойства: 1. Число исходов конечное; 2. Приблизительное значение.

6.Классическое определение вероятности, ее свойства.

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия.

С в о й с т в о 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,

Р (A) = m / n = n / n = 1.

С в о й с т в о 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

Р (А) = m / n = 0 / n = 0.

С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m / n < 1, следовательно,

0 <Р (А) < 1

7. Геометрическое определение вероятности.Предположим, что на отрезок длины 4 на удачу бросают точку. Вероятность попадания точки в любую часть отрезка пропорциональна длине этой части отрезка и не зависит от её месторасположения.

Вероятность не зависит от месторасположения и термин участка S.

3)Для объема : р=v/V

8. Аксиоматическое определение вероятности.Вероятностью наз-сячисловая ф-ция, определенная на поле событий S и обладающая след. Действиями: Аксиома 1.Для любого события А принадлежит S. Р(А)>=0. Аксиома 2.Вероятность достоверного события =1.Аксиома 3.Вероятность объединения двух несовместных соб-й равна сумме вер-й этих соб-й.А*В=0, Р(А+В)=Р(А)+Р(В).

9. Теорема сложения вероятностей и следствия из нее. Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Определение. Противоположными называются два несовместных события, образующие полную группу. Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Следствие 2: Сумма вероятностей противоположных событий равна единице.

10. Условная вероятность, ее свойства.Условная вероятность — вероятность одного события при условии, что другое событие уже произошло. Пусть (амегабольшая, F, P) - фиксированное вероятностное пространство. Пусть А, В принадлежит F суть два случайных события, причём Р(В)>0 . Тогда условной вероятностью события А при условии события В наз-я Р(А|B)=P(A∩В)/P(B)

Свойства условных вероятностей

Всегда 0<=Р(А/B)<=1 причем Р(А/B)=0 если АВ - невозможное событие, и Р(А/B)=1 если (А включено в В).

Если C=AUB и AB= Ø то для любого события D P(A/D)+P(B/D)=P(C/D)

Если событие (не) А, противоположное A, то P(A/B)=1- (не) Р(А/B).

11. Независимые события. Попарно независимые события. События независимые в совокупности.Соб-я А и В наз-ся независимыми, если вероятность наступления одного из них не зависит от того, что произошло или не произошло второе соб-е. события попарно независимы, если любые два события из этого семейства независимы, то есть Р(Аi ∩ Aj)=P(Ai)*P(Aj). события совместно независимы, если для любого конечного набора событий верно Р(Ai1 ∩… ∩Ajn)= Р(Ai1)…P(Ajn). Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.

12. Теорема умножения вероятностей и следствия из нее.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В). Следствие 1. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий: Р (АВ) = Р(А) · Р(В). Следствие 2. При производимых n одинаковых независимых испытаниях, в каждом из которых события А появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)n

13 Формула полной вероятности. Формула Байеса.

Теорема: вероятность события A, которое может наступить в результате появления одного из K несовместных событий, образующих полную группу равна p(A)=∑ki=1p(Bi)p(A∖Bi) сумме произведений вероятности каждого из этих событий на условную вероятность события A. Bi - гипотезы, ∑ki=1p(Bi)=1

Доказательство.

A=AB1+AB2+...ABk p(A)=p(AB1+AB2+...ABk)=p(AB1)+p(AB2)+...p(ABk), поскольку событияAB1,AB2,...,ABk - несовместные. В силу того, что p(ABi)=p(Bi)p(A∖Bi) ,p(A)=p(B1)p(A∖B1)+p(B2)p(A∖B2)+...p(Bk)p(A∖Bk)=∑ki=1p(Bi)p(A∖Bi)

ЧТД

Изменится ли вероятность гипотез после того, как появилась информация что событие A уже произошло.

p(A)p(Bi∖A)=p(Bi)p(A∖Bi) отсюда p(Bi∖A)=p(Bi)p(A∖Bi)∑ki=1p(Bi)p(A∖Bi) - формула Байеса (вероятность уточненной гипотезы)

14.Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях; по формуле Байеса можно пересчитывать вероятность, беря в учет как ранее известную информацию, так и данные новых наблюдений.

Математическая формулировка

,

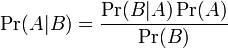где

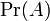— априорная вероятность гипотезы A;

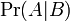— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

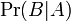— вероятность наступления события B при истинности гипотезы A;

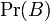— вероятность наступления события B.