Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Основные понятия теории вероятностей
Классификация событий на возможные, вероятные и случайные. Понятия простого и сложного элементарного события. Операции над событиями. Классическое определение вероятности случайного события и её свойства. Элементы комбинаторики в теории вероятностей. Геометрическая вероятность. Аксиомы теории вероятностей.
Классификация событий
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Примеры событий:
– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).
Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита 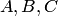 и т.д.
и т.д.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие  — выпадание трех очков на первой игральной кости, событие
— выпадание трех очков на первой игральной кости, событие 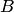 — выпадание трех очков на второй кости.
— выпадание трех очков на второй кости.  и
и 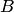 — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие
— совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие  — наудачу взятая коробка окажется с обувью черного цвета, событие
— наудачу взятая коробка окажется с обувью черного цвета, событие 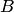 — коробка окажется с обувью коричневого цвета,
— коробка окажется с обувью коричневого цвета,  и
и 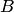 — несовместные события.
— несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера.  — появление красного шара при одном извлечении,
— появление красного шара при одном извлечении, 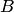 — появление белого шара,
— появление белого шара, 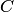 — появление шара с номером. События
— появление шара с номером. События 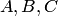 образуют полную группу совместных событий.
образуют полную группу совместных событий.
Введем понятие противоположного, или дополнительного, события. Под противоположным событием 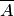 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие  . Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие
. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие  , либо бракованным — событие
, либо бракованным — событие 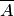 .
.
Операции над событиями
При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий.
Свойства вероятности
Свойство 1. Если все случаи являются благоприятствующими данному событию  , то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления
, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 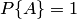 , так как в этом случае
, так как в этом случае 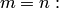
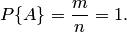
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию  , то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления
, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 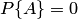 , так как в этом случае
, так как в этом случае 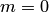 :
:
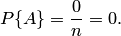
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 4. Вероятность наступления противоположного события 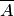 определяется так же, как и вероятность наступления, события
определяется так же, как и вероятность наступления, события  :
:
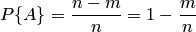
где 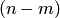 — число случаев, благоприятствующих появлению противоположного события
— число случаев, благоприятствующих появлению противоположного события 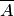 . Отсюда вероятность наступления противоположного события
. Отсюда вероятность наступления противоположного события 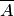 равна разнице между единицей и вероятностью наступления события
равна разнице между единицей и вероятностью наступления события  :
:
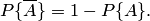
| (1.2) |
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим  событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию
событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию  лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
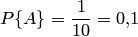 .
.
Элементы комбинаторики
В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество 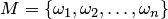 , то размещением (сочетанием) из
, то размещением (сочетанием) из 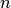 элементов по
элементов по 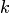 называется любое упорядоченное (неупорядоченное) подмножество
называется любое упорядоченное (неупорядоченное) подмножество 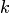 элементов множества
элементов множества 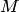 . При
. При 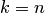 размещение называется перестановкой из
размещение называется перестановкой из 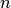 элементов.
элементов.
Пусть, например, дано множество 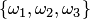 . Размещениями из трех элементов этого множества по два являются
. Размещениями из трех элементов этого множества по два являются 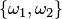 ,
, 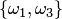 ,
, 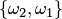 ,
, 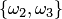 ,
, 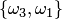 ,
, 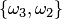 ; сочетаниями —
; сочетаниями — 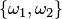 ,
, 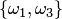 ,
, 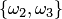 .
.
Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из 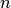 элементов по
элементов по 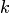 вычисляется по формуле
вычисляется по формуле
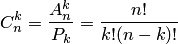 ,
,
где
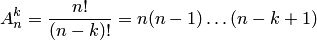
есть число размещений из 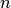 элементов по
элементов по 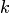 ;
; 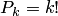 — число перестановок из
— число перестановок из 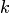 элементов.
элементов.
Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.
Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно 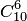 — числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию
— числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию  (среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей
(среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей 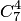 способами; при этом остальные
способами; при этом остальные 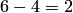 детали должны быть нестандартными; взять же 2 нестандартные детали из
детали должны быть нестандартными; взять же 2 нестандартные детали из 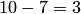 нестандартных деталей можно
нестандартных деталей можно 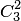 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 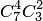 . Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
. Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
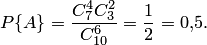
Геометрическая вероятность
В классическом определении вероятности рассматривается полная группа конечного числа равновозможных событий. На практике очень часто число возможных исходов испытаний бесконечно. В таких случаях классическое определение вероятности неприменимо. Однако иногда в подобных случаях можно воспользоваться другим методом вычисления вероятности. Для определенности ограничимся двумерным случаем.
Пусть на плоскости задана некоторая область 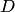 площадью
площадью 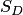 , в которой содержится другая область
, в которой содержится другая область 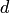 площадью
площадью 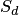 (рис. 3). В область
(рис. 3). В область 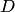 наудачу бросается точка. Чему равна вероятность того, что точка попадет в область
наудачу бросается точка. Чему равна вероятность того, что точка попадет в область 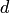 ? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области
? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области 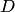 , и вероятность попасть в какую-либо часть области
, и вероятность попасть в какую-либо часть области 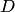 пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область
пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область 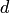 при бросании наудачу точки в область
при бросании наудачу точки в область 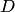
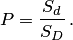
| (1.3) |
Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.
Пример 3. Круглая мишень вращается с постоянной угловой скоростью. Пятая часть мишени окрашена в зеленый цвет, а остальная — в белый (рис. 4). По мишени производится выстрел так, что попадание в мишень — событие достоверное. Требуется определить вероятность попадания в сектор мишени, окрашенный в зелёный цвет.
Решение. Обозначим  — "выстрел попал в сектор, окрашенный в зелёный цвет". Тогда
— "выстрел попал в сектор, окрашенный в зелёный цвет". Тогда 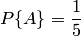 . Вероятность получена как отношение площади части мишени, окрашенной в зелёный цвет, ко всей площади мишени, поскольку попадания в любые части мишени равновозможны.
. Вероятность получена как отношение площади части мишени, окрашенной в зелёный цвет, ко всей площади мишени, поскольку попадания в любые части мишени равновозможны.
Аксиомы теории вероятностей
Из статистического определения вероятности случайного события следует, что вероятность события есть число, около которого группируются частоты этого события, наблюдаемые на опыте. Поэтому аксиомы теории вероятностей вводятся так, чтобы вероятность события обладала основными свойствами частоты.
Аксиома 1. Каждому событию  соответствует определенное число
соответствует определенное число 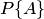 , удовлетворяющее условию
, удовлетворяющее условию 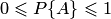 и называемое его вероятностью.
и называемое его вероятностью.
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3. Вероятность невозможного события равна нулю.
Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей.
Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Формула полной вероятности
Теорема 2.5. Если событие  наступает только при условии появления одного из событий
наступает только при условии появления одного из событий 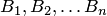 , образующих полную группу несовместных событий, то вероятность события
, образующих полную группу несовместных событий, то вероятность события  равна сумме произведений вероятностей каждого из событий
равна сумме произведений вероятностей каждого из событий 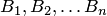 на соответствующую условную вероятность события
на соответствующую условную вероятность события 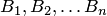 :
:
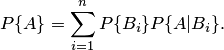
| (2.1) |
При этом события 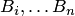 называются гипотезами, а вероятности
называются гипотезами, а вероятности 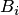 — априорными. Эта формула называется формулой полной вероятности.
— априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим  событие, означающее годность собранного узла;
событие, означающее годность собранного узла; 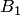 ,
, 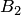 и
и 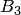 — события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
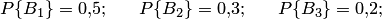
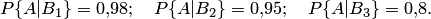
Искомая вероятность
Формула Байеса
Эта формула применяется при решении практических задач, когда событие  , появляющееся совместно с каким-либо из событий
, появляющееся совместно с каким-либо из событий 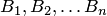 , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез 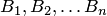 . Априорные (до опыта) вероятности
. Априорные (до опыта) вероятности 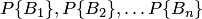 известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности 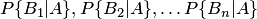 . Для гипотезы
. Для гипотезы 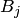 формула Байеса выглядит так:
формула Байеса выглядит так:
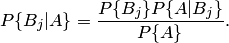
Раскрывая в этом равенстве 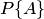 по формуле полной вероятности (2.1), получаем
по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка
для второго станка
для третьего станка
Основные понятия теории вероятностей
Классификация событий на возможные, вероятные и случайные. Понятия простого и сложного элементарного события. Операции над событиями. Классическое определение вероятности случайного события и её свойства. Элементы комбинаторики в теории вероятностей. Геометрическая вероятность. Аксиомы теории вероятностей.
Классификация событий
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Примеры событий:
– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).
Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита 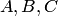 и т.д.
и т.д.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие  — выпадание трех очков на первой игральной кости, событие
— выпадание трех очков на первой игральной кости, событие 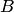 — выпадание трех очков на второй кости.
— выпадание трех очков на второй кости.  и
и 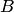 — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие
— совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие  — наудачу взятая коробка окажется с обувью черного цвета, событие
— наудачу взятая коробка окажется с обувью черного цвета, событие 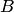 — коробка окажется с обувью коричневого цвета,
— коробка окажется с обувью коричневого цвета,  и
и 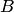 — несовместные события.
— несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера.  — появление красного шара при одном извлечении,
— появление красного шара при одном извлечении, 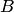 — появление белого шара,
— появление белого шара, 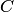 — появление шара с номером. События
— появление шара с номером. События 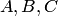 образуют полную группу совместных событий.
образуют полную группу совместных событий.
Введем понятие противоположного, или дополнительного, события. Под противоположным событием 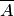 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие  . Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие
. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие  , либо бракованным — событие
, либо бракованным — событие 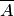 .
.
Операции над событиями
При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий.
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Сумма 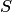 событий
событий 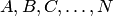 обозначается так:
обозначается так:
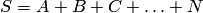 .
.
Например, если событие  есть попадание в цель при первом выстреле, событие
есть попадание в цель при первом выстреле, событие 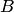 — при втором, то событие
— при втором, то событие 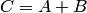 есть попадание в цель вообще, безразлично, при каком выстреле — первом, втором или при обоих вместе.
есть попадание в цель вообще, безразлично, при каком выстреле — первом, втором или при обоих вместе.
