Задача 11. Обработка двухмерной выборки

Условие задачи

По выборке двухмерной случайной величины:

- вычислить точечную оценку коэффициента корреляции;

- вычислить интервальную оценку коэффициента корреляции (γ = 0,95);

- проверить гипотезу об отсутствии корреляционной зависимости;

- вычислить оценки параметров a₀ и a₁ линии регрессии ;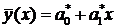

- построить диаграмму рассеивания и линию регрессии.

Необходимая для выполнения задачи выборка, объемом 25 пар значений двумерной величины, содержится в индивидуальном задании студента.

Методические указания

Пусть проводится n независимых опытов, в каждом из которых двухмерная случайная величина (X,Y) принимает определенные значения и результаты опытов представляют собой двухмерную выборку вида

Статистическая обработка двухмерных массивов данных включает в себя обработку и анализ составляющих X и Y как одномерных величин, и вычисление оценок и анализ параметров, присущих только двухмерным (многомерным) случайным величинам.

Как правило, определяются следующие оценки:

– математических ожиданий случайных величин X и Y:

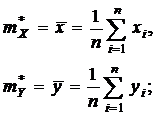(11.1)

– дисперсий случайных величин X и Y:

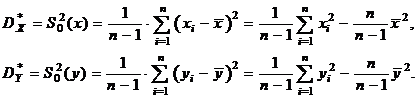(11.2)

Состоятельная несмещенная оценка корреляционного момента равна

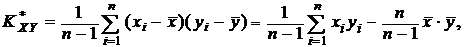(11.3)

где – значения, которые приняли случайные величины X и Y в i-м опыте;

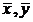– средние значения случайных величин X и Y соответственно.

Состоятельная оценка коэффициента корреляции равна

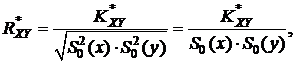(11.4)

где 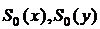– оценки среднеквадратического отклонения случайных величин X и Y соответственно.

Доверительный интервал для коэффициента корреляции с надежностью γ для случая двумерного нормального распределения имеет вид

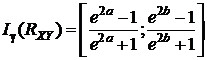(11.5)

где ;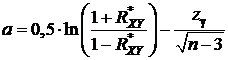

;

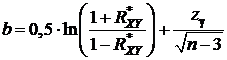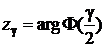– значение аргумента функции Лапласа, т.е. .

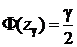Гипотеза об отсутствии корреляционной зависимости. Предполагается, что двухмерная случайная величина (X, Y) распределена по нормальному закону. Алгоритм проверки следующий.

1. Формулируется гипотеза:

: ;

: .

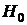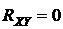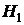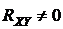Здесь 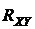– теоретический коэффициент корреляции.

2. Вычисляется оценка коэффициента корреляции 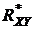по формуле (11.4).

3. Если объем выборки не велик ( n < 50 ), то определяется значение критерия

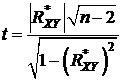, (11.6)

который распределен по закону Стьюдента с 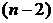степенями свободы, если гипотеза 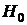верна.

4. По заданному уровню значимости a вычисляется доверительная вероятность 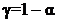и из таблицы Стьюдента выбирается критическое значение 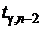(см. Приложение 3).

5. Если 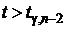, то гипотеза 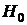отклоняется, т.е. величины X, Y коррелированны. В противном случае гипотеза 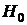принимается.

3*. Если объем выборки велик (n ≥ 50 ), то определяется значение критерия

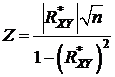, (11.7)

который распределен по нормальному закону, если гипотеза 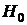верна.

4*. По заданному уровню значимости a из таблицы функции Лапласа определяется критическое значение 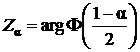, т.е. 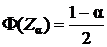(см. Приложение 2).

5*. Если 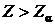, то гипотеза 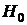отклоняется, а следовательно, величины X, Y коррелированны. В противном случае гипотеза 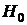принимается.