Контрольная работа №1. Теория вероятностей

Типовой расчет

Для студентов всех специальностей очной формы обучения

Минск 2011

ТИПОВОЙ РАСЧЕТ

Указания по выбору варианта

Рабочей программой дисциплины «Теория вероятностей и математическая статистика» предусмотрено выполнение типового расчета, состоящего из двух контрольных работ. Контрольная работа по теории вероятностей состоит из 9 контрольных задач (№1 - 9), а контрольная работа по математической статистике из 2 контрольных задач (№10-11). Варианты задач контрольной работы по теории вероятностей и выборки для контрольной работы по математической статистике содержатся в индивидуальном задании, которое студент получает у преподавателя ведущего практические занятия.

Задания по курсу ТВ и МС формируются специальной программой и содержат случайно выбранные варианты девяти задач по теории вероятностей, выборку одномерной случайной величины для задачи 10 и выборку двумерной случайной величины для задачи 11.

Контрольная работа №1. Теория вероятностей

Методические указания

Случайное событие – любой факт в опыте со случайным исходом, который может произойти или не произойти. Любое случайное событие А, возможное в данном опыте, есть некоторое подмножество универсального множества 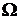исходов этого опыта.

Событие А называется достоверным, если 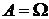, т.е. происходит в каждом опыте.

Событие А называется невозможным, если 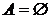, т.е. никогда не происходит в данном опыте.

Противоположнымсобытием 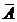называется событие, которое происходит тогда, когда не происходит событие А.

Суммой или объединением двух событий А и В (обозначается 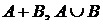) называется событие, состоящее в появлении или события А, или событии В, или А и В одновременно.

Произведением или пересечением двух событий А и В (обозначается 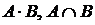) называется событие, состоящее в появлении и события А, и события В одновременно или совместно.

Несовместными событиями А и В называются такие, которые не могут произойти одновременно в одном опыте. Для несовместных событий .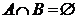

Аксиома 1.Вероятность p(А) случайного события А есть функция множества элементарных исходов, благоприятных событию А, и вероятность любого события принимает значения

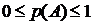, (1.1)

причем .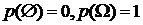

Аксиома 2.Вероятность суммы несовместных случайных событий равна сумме вероятностей этих событий:

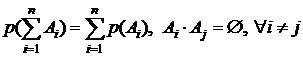(1.2)

Следствие аксиом 1 и 2: Вероятность прямого события 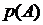и вероятность противоположного события 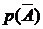связаны соотношением

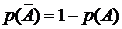. (1.3)

Классическое определение вероятности: вероятность события А определяется по формуле

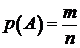, (1.4)

где n – число всех возможных, равновероятных исходов данного опыта;

m – число исходов, благоприятствующих появлению события.

Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области равноправны в отношении попадания точки T.

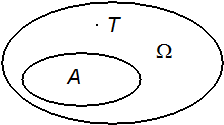
Рис. 1.1

Тогда за вероятность попадания точки T в область A принимается отношение

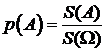, (1.5)

где S(A) и S() — геометрические меры (длина, площадь, объем и т.д.) областей A и соответственно.

Примеры

Пример 1.1. Какова вероятность того, что наудачу взятый телефонный номер из 7 цифр имеет все цифры различные.

Решение. Определим событие А. Событие А состоит в том, что в семизначном номере все цифры различны. Так как номер семизначный, а цифр всего 10, то общее число исходов n опыта равно числу размещений c повторением элементов из 10 по 7: 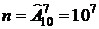. Для подсчета благоприятствующих исходов подходит формула для размещений без повторения элементов : 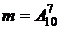. Тогда

.

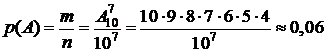Пример 1.2. Наудачу взяты два положительных числа x и y, причем 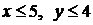. Найти вероятность того, что 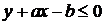и 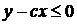, если .

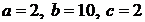Решение. Подставляя значения коэффициентов в неравенства, получаем:

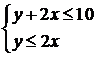(1.11)

Строим на рис. 1.2 оси координат и область, которая определяет пространство элементарных событий Ω. Она задается неравенствами 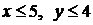и на рисунке 1.2 отображается в виде прямоугольника.

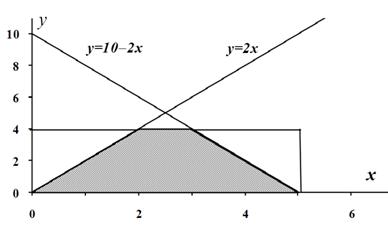
Рис. 1.2.

Площадь прямоугольника 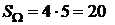. Область благоприятствующих исходов определяется неравенствами (1.11), поэтому строим на рисунке прямые, которые задаются неравенствами (1.11). Заштрихованная на рисунке 1.2 область и описывает благоприятствующие исходы (с учетом всех возможных значений), площадь этой заштрихованной трапеции равна 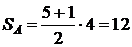[у. е.]. Тогда вероятность события А равна

.

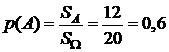Примеры

Пример 2.1. Вычислительная машина (ВМ) состоит из n блоков. Вероятность безотказной работы в течении времени Т (надежность) первого блока равна p₁ , второго – p₂ , и т.д. Блоки отказывают независимо друг от друга. При отказе любого блока отказывает ВМ. Найти вероятность того, что ВМ откажет за время Т.

Решение. Рассмотрим события А₁ – отказывает 1-й блок, А₂ – отказывает 2-й блок и т.д.. Пусть событие В – отказ вычислительной машины. Это событие произойдет тогда, когда выполнится или событие А₁ , или событие А₂ и т.д.. Видим, что следует применять теорему о сумме или объединении n произвольных событий, формула (2.3):

.

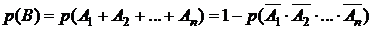События A_i являются независимыми, поэтому правая часть запишется в виде:

.

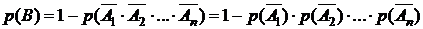Вероятности противоположных событий 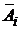(здесь событие 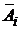‑ i-й блок работает) даны в условии, т.е. 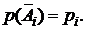Окончательно получаем

.

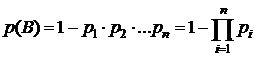Пример 2.2. Дана схема электрической цепи (рис. 2.1).

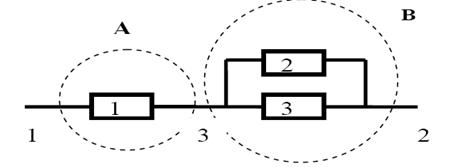
Рис. 2.1

Вероятности работы элементов цепи 1, 2, 3 соответственно равны 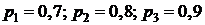. Элементы цепи отказывают независимо друг от

друга. Найти вероятность того, что ток пройдет из точки 1 в точку 2.

Решение. Опишем через события работу элементов цепи. Пусть событие А₁ состоит в том, что работает элемент 1, событие А₂ – элемент 2, событие А₃ –элемент 3. Тогда вероятности этих событий запишутся так: 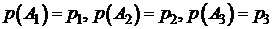. Найдем вероятности противоположных событий (т.е. того, что элементы 1, 2, 3 не работают и ток через них не идет), используя (1.3):

.

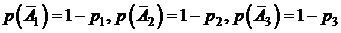Анализируем заданную цепь и определяем участки цепи с последовательным и параллельным соединением. На рис. 2.1 элементы 2, 3 соединены параллельно. А элемент 1 соединен последовательно с элементами 2, 3. Поэтому введем событие А состоящее в том, что ток пройдет из точки 1 в точку 3, оно выполнится тогда, когда будет работать элемент 1. Можно записать: А=А₁. Введем событие В, состоящее в том, что ток пройдет из точки 2 в точку 3; оно произойдет тогда, когда будут работать или элемент 2, или элемент 3. Тогда событие В можно описать так: 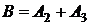. Рассмотрим событие С состоящее в том, что ток пройдет из точки 1 в точку 2, оно выполнится тогда, когда выполнится и событие А и событие В. Событие С запишется так: 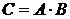. По условию задачи необходимо найти вероятность события С (учтем, что события А и В независимы), используем (2.5):

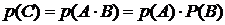(2.8)

Найдем вероятности событий, входящих в правую часть формулы (2.8):

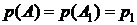, а 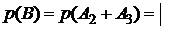см. формулу (2.3)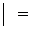

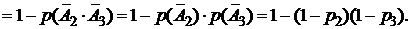
Подставляя полученные значения в формулу (2.8), получим

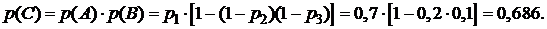
Методические указания

Пусть проводится опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез) 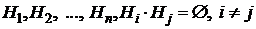, образующих полную группу 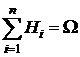. Каждая из гипотез осуществляется случайным образом и представляет собой случайное событие. Вероятности гипотез известны и равны:

.

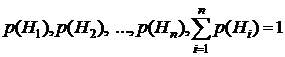Рассмотрим некоторое событие А, которое может появиться только вместе с одной из гипотез. Известны условные вероятности события А для каждой из гипотез:

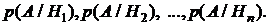
Тогда полная вероятность события A определяется по формуле

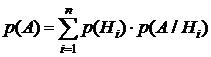. (3.1)

Пусть до проведения некоторого опыта об его условиях n можно сделать n исключающих друг друга предположений (гипотез) 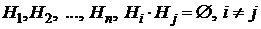, образующих полную группу 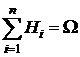. Вероятности гипотез p(H₁), p(H₂), … p(H_n) до опыта (априорные вероятности) известны, причем .

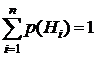Опыт произведен, и произошло некоторое событие А. Тогда определить апостериорные (послеопытные) вероятности гипотез с учетом того, что произошло именно событие А 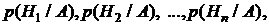можно определить по формуле Байеса

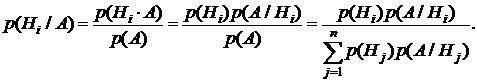(3.2)

Примеры

Пример 3.1. Радиоприемное устройство имеет блок обработки сигналов, который позволяет отделить полезный сигнал от помехи без искажений. Если отношение уровня сигнала к уровню помехи менее 1,2, то вероятность выделить полезный сигнал без искажений равна 0,1, если отношение уровня сигнала к уровню помехи от 1,2 до двух, то вероятность – 0,8, а если превышает 2, то вероятность равна 1. Приемник принял сигнал, причем поступление сигнала с помехой любого уровня равновероятно. Найти вероятность того, что он будет обработан без искажений.

Решение. Определим событие А – приемник обработал сигнал без искажений. Выдвигаем гипотезы: H₁ – приемник принял сигнал с отношение уровня сигнала к уровню помехи менее 1,2; H₂ – приемник принял сигнал с отношение уровня сигнала к уровню помехи от 1,2 до двух; H₃ – приемник принял сигнал с отношение уровня сигнала к уровню помехи более двух. Вероятности гипотез (т.к. по условию они равновероятны): 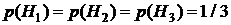. Определим условные вероятности события А при каждой гипотезе: 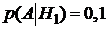, , 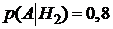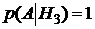. По формуле полной вероятности (3.1) найдем вероятность события А :

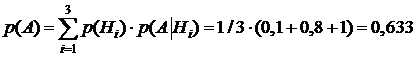
Пример 3.2. Прибор состоит из двух блоков, работа каждого блока необходима для работы прибора. Вероятность безотказной работы в течении времени Т (надежность) первого блока равна р₁ , второго – р₂. Прибор испытывался в течении времени Т и отказал. Найти вероятность того, что отказал только первый блок, а второй исправен (р₁= 0,5; р₂ = 0,7).

Решение. Сформулируем событие А – оно состоит в том, что прибор отказал. Это событие может произойти при таких гипотезах: H₁ – отказал только первый блок, а второй исправен; H₂ – отказал второй блок, а первый исправен; H₃ – отказал первый блок, отказал второй блок ; H₄ – работает первый блок, работает второй блок. Как видим, гипотезы описывают сложные события. Для упрощения расчета вероятностей этих событий введем такие события: событие В₁ – работает первый блок; событие В₂ – работает второй блок. Тогда гипотезу H₁ через эти события можно описать так: 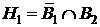, где 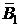‑ противоположное событие, т.е. что блок не работает. Аналогично распишем и другие гипотезы: 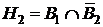, , 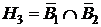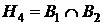. Так как события 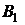и 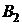независимы, то вероятностей гипотез рассчитаем, используя теорему умножения вероятностей для независимых событий (2.5):

,

,

,

.

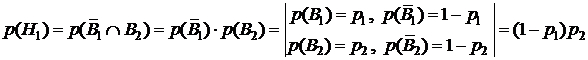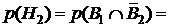
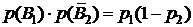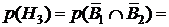
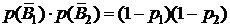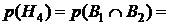
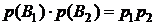Необходимо найти условные вероятности события А при каждой гипотезе.

Тогда 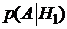‑ это условная вероятность того, что прибор вышел из строя, при условии, что первый блок отказал, а второй исправен. Видим, что событие А всегда произойдет, если блок отказал, т.е. А – достоверное событие. Поэтому 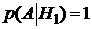. Аналогично 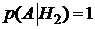, 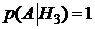. А вот при четвертой гипотезе событие А никогда не выполнится, здесь А – невозможное событие и вероятность его .

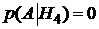Из условия задачи следует, что необходимо пересмотреть вероятность первой гипотезы, поэтому запишем формулу Байеса для первой гипотезы: 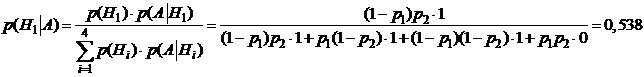Из полученного решения следует, что до появления события А вероятность гипотезы H₁ была равна 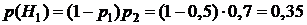. А с учетом появления события А изменилась значительно, стала равной 0,538.

Задача 4. Формула Бернулли

Условия вариантов задачи

Ниже приведены 40 вариантов задачи 4. Номер варианта задачи, которую студент должен решить, указан в индивидуальном задании.

4.1. Вероятность изготовления стандартного изделия равна 0,95. Какова вероятность того, что среди десяти изделий не более одного нестандартного?

4.2. Вероятность попадания в мишень при одном выстреле равна 0,6. По мишени производится четыре независимых выстрела. Найти вероятность того, что будет хотя бы одно попадание в мишень.

4.3. Техническая система состоит из пяти узлов. Вероятность отказа в течение времени t для каждого узла равна 0,2. Система выходит из строя, если откажут три и более узлов. Найти вероятность выхода из строя этой системы за время t, если отказы в узлах происходят независимо друг от друга.

4.4. Игральную кость подбрасывают 12 раз. Чему равно наивероятнейшее число выпадений 6?

4.5. Вероятность изготовления изделия отличного качества равна 0,9. Сколько надо должно быть деталей в партии, чтобы наивероятнейшее число изделий отличного качества было равно 10?

4.6. По данным технического контроля в среднем 2% изготавливаемых на заводе автоматических станков нуждается в дополнительной регулировке. Чему равна вероятность того, что из шести изготовленных станков четыре нуждаются в дополнительной регулировке?

4.7. Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что в течение часа этих требований будет от трех до пяти.

4.8. В мастерской работает десять моторов. Вероятность того, что мотор работает с полной нагрузкой, равна 0,8. Найти вероятность того, что в данный момент времени не менее восьми моторов работает с полной нагрузкой.

4.9. Вероятность появления события А в каждом из 15 независимых опытов равна 0,3. Определить вероятность появления события А по крайней мере два раза.

4.10. Вероятность появления события С в каждом из 10 независимых опытов равна 0,2. Определить вероятность появления события С хотя бы восемь раз.

4.11. Монету подбрасывают восемь раз. Чему равно наивероятнейшее число выпадений герба?

4.12. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,3. Произведено 12 бросков. Найти вероятность того, что будет 10 попаданий.

4.13. Определить вероятность того, что в семье, имеющей пять детей, будет три девочки и два мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

4.14. Монету подбрасывают восемь раз. Какова вероятность того, что шесть раз она упадет гербом вверх?

4.15. В результате многолетних наблюдений установлено, что вероятность выпадения снега 12 октября в данном городе равна 1/3. Сколько лет должны проводиться метеонаблюдения, чтобы наивероятнейшее число снежных дней 12 октября в данном городе было равно 20.

4.16. Имеется 20 ящиков однородных деталей. Вероятность того, что в одном взятом наудачу ящике детали окажутся стандартными, равна 0,75. Найти наивероятнейшее число ящиков, в которых все детали стандартные.

4.17. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что в мишени будет одно или два попадания.

4.18. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что в мишени будет три попадания.

4.19. Монету подбрасывают восемь раз. Какова вероятность того, что она ни разу не упадет гербом вверх?

4.20. При установившемся технологическом процессе 90% всей произведенной продукции оказывается продукцией высшего сорта. Сколько изделий должно находиться в ящике, чтобы наивероятнейшее число изделий высшего сорта в ящике составило 340 изделий.

4.21. Монету подбрасывают восемь раз. Какова вероятность того, что она четыре раза упадет гербом вверх?

4.22. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,9. Произведено 12 бросков. Найти вероятность того, что будет 11 или 12 попаданий.

4.23. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет хотя бы одно попадание в мишень.

4.24. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет хотя бы пять попаданий в мишень.

4.25. Монету подбрасывают десять раз. Какова вероятность того, что она упадет гербом вверх от трех до пяти раз?

4.26. Монету подбрасывают 100 раз. Какова вероятность того, что она ни разу не упадет гербом вверх?

4.27. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,95. Произведено десять бросков. Найти вероятность того, что будет девять попаданий.

4.27. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,9. Произведено 12 бросков. Найти вероятность того, что будет не менее 11 попаданий.

4.29. Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что в течение часа будет хотя бы одно требование.

4.30. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится восемь независимых выстрелов. Найти вероятность того, что будет от четырех до шести попаданий в мишень.

4.31. Вероятность изготовления изделия отличного качества равна 0,9. Изготовлено 50 изделий. Чему равны наивероятнейшее число изделий отличного качества и вероятность такого числа изделий отличного качества?

4.32. Вероятность появления события А в каждом из 15 независимых опытов равна 0,3. Определить вероятность появления события А семь или восемь раз.

4.33. В результате многолетних наблюдений установлено, что вероятность выпадения дождя 1 октября в данном городе равна 1/7. Определить наивероятнейшее число дождливых дней 1 октября в данном городе за 40 лет.

4.34. При установившемся технологическом процессе 80% всей произведенной продукции оказывается продукцией высшего сорта. Какое количество изделий должно быть в партии, чтобы наивероятнейшее число изделий высшего сорта в партии составляло 250 изделий.

4.35. Монету подбрасывают восемь раз. Какова вероятность того, что она ни разу не упадет гербом вверх?

4.36. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет шесть попаданий в мишень.

4.37. Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,5. Произведено 10 бросков. Найти вероятность того, что будет не менее 8 попаданий.

4.38. Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,1. Найти вероятность того, что в течение часа поступит два или три требования.

4.39. Имеется 10 ящиков однородных деталей. Вероятность того, что в одном взятом наудачу ящике детали окажутся стандартными, равна 0,9. Найти вероятность, что хотя бы в одном ящике все детали будут стандартными.

4.40. Монету подбрасывают восемь раз. Какова вероятность того, что шесть раз она упадет гербом вверх?

Методические указания

Пусть производится n независимых опытов. В результате каждого опыта событие A появляется в одном опыте с вероятностью р и не появляется с вероятностью 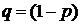. Вероятность того, что в последовательности из n опытов событие А произойдет ровно k раз, вычисляется по формуле Бернулли:

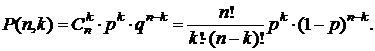(4.1)

Рекуррентная формула 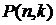имеет вид

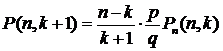(4.2)

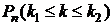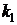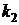Вероятность того, что в n опытах схемы Бернулли событие А появится от до раз ( 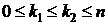), равна

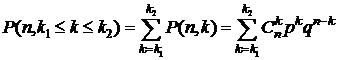. (4.3)

Вероятность того, что при n независимых испытаниях событие А появится не менее m раз, вычисляется так:

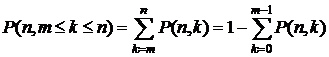(4.4)

Здесь надо выбирать, какой ряд короче, и его использовать для расчета. Например, вероятность того, что в n опытах событие А появится хотя бы один раз, равна

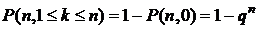. (4.5)

Наивероятнейшее число 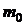наступлений события А при n опытах определяется из неравенства:

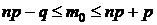(4.6)

Примеры

Пример 4.1. По каналу связи передается n = 6 сообщений, каждое из которых независимо от других с вероятностью p = 0,2 оказывается искаженным. Найти вероятности следующих событий:

A = {ровно два сообщения из 6 искажены},

B = {все сообщения будут искажены},

C = {все сообщения будут переданы без искажений},

D = {не менее двух сообщений из 6 искажены}.

Решение. По формуле Бернулли (4.1) рассчитаем вероятности первых трех событий:

,

.

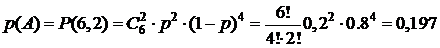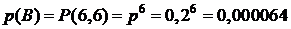
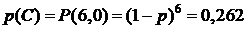Вероятность события D определим по формуле (4.4), первый ряд требует для вычисления пяти слагаемых, второй только два:

.

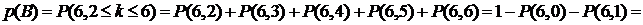
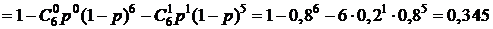Пример 4.2. Монету подбрасывают 10 раз. Чему будет равно наивероятнейшее число выпадений герба?

Решение. Запишем 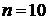, вероятность появления герба (событие А) симметричной монеты равна 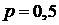. Вероятность противоположного события 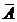: 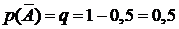. Тогда наивероятнейшее число 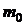определим, используя (4.6):

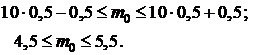
Отсюда следует, что .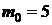

Методические указания

Случайная величина (СВ) – это величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее до опыта неизвестно, какое именно. Обозначения случайной величины: X, Y; а их значения: x, y.

Случайная величина Х называется дискретной, если ее множество возможных значений W_X – счетное, т.е. элементы множества можно расположить в определенном порядке и пронумеровать.

Закон распределения случайной величины — любое правило, устанавливающее соответствие между значениями случайной величины и вероятностями ее наступления.

Рядом распределения дискретной СВ X называется таблица, в верхней строке которой перечислены все возможные значения СВ 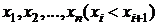, а в нижней — вероятности их появления 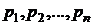, где :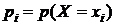

			...
			...

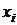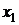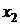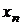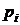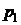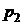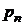Так как события 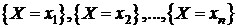несовместны и образуют полную группу, то справедливо контрольное соотношение

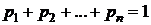. (5.1)

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент x функции F(x): .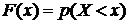

Свойства функции распределения:

1. F(- ) = 0 и F(+ ) = 1.

2. Неубывающая функция: .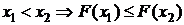

4. Вероятность попадания значения СВ X в интервал :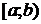

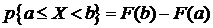(5.2)

Функция распределения дискретной СВ определяется так:

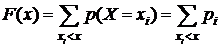(5.3)

где 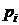– вероятности ряд распределения этой СВ.

Здесь суммируются вероятности всех тех значений 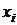, которые по своей величине меньше, чем x – аргумент функции F(x).

				...
				...

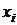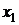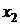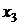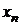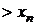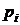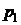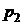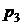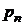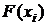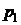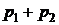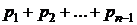Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений.

Математическое ожидание характеризует среднее значение случайной величины и для дискретной СВ определяется по формуле

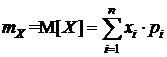(5.4)

Как видно из (5.4), в качестве математического ожидания СВ используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения.

Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для дискретной СВ определяется по формуле:

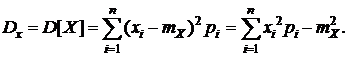(5.5)

Примеры

Пример 5.1. По командному пункту противника производится пуск трех ракет, причем вероятность попадания в цель при пуске одной ракеты равна 0,8. Построить ряд распределения числа попаданий.

Решение. Определим случайную величину X как число попаданий в цель при трех пусках ракет. Эта случайная величина может принимать следующие значения: 0, 1, 2, 3. Найдем вероятность принятия величиной X этих значений, используя формулу Бернулли:

,

,

,

.

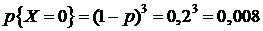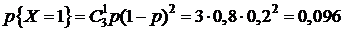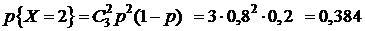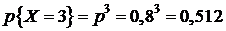Ряд распределения имеет следующий вид

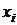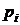	0,008	0,096	0,384	0,512

Как видим, условие (5.1) выполняется.

Пример 5.2. Зная ряд распределения для случайной величина X , описанной в примере 5.1, построить график функции распределения. Найти математическое ожидание и дисперсию дискретной случайной величины X.

Решение. Рассчитаем значения функции распределения для фиксированных значений 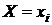, взятых из ряда распределения (пример 5.1).

1. .

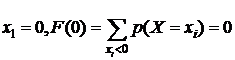2.

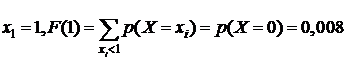
3. .

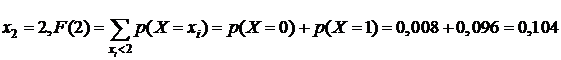4.

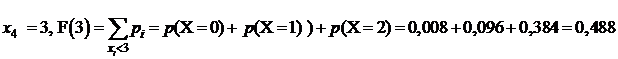
5. При 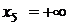, согласно свойствам функции распределения,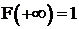

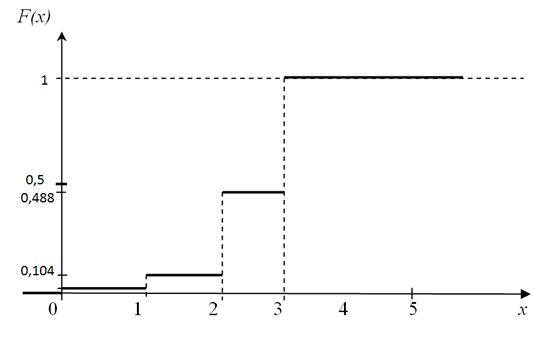
Рис. 5.1

Опишем построение графика функции распределения F(x) (рис. 5.1). Рассмотрим первый промежуток по оси Х от 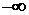до 0; согласно пункту 1 значение 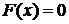и линия идет по оси Х до нуля включительно. Второй промежуток по оси Х от 0 до 1; согласно пункту 2 значение 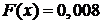значит проводим ступеньку высотой 0,008. Третий промежуток от 1 до 2; согласно пункту 3 значение 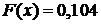значит проводим ступеньку высотой 0,104. Четвертый промежуток от 2 до 3; согласно пункту 4 значение 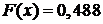значит проводим ступеньку высотой 0,488. Пятый промежуток от 3 до 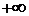; согласно пункту 5 значение 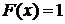значит проводим ступеньку высотой 1.

Математическое ожидание дискретной СВ X определим по формуле (5.4):

,

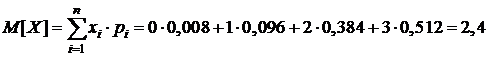Дисперсию дискретной СВ X определим по формуле (5.5):

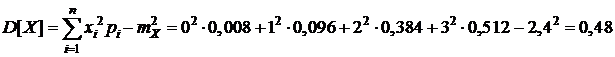
Методические указания

Случайная величина Х называется непрерывной, если ее функция распределения F(x) – непрерывная и дифференцируемая функция для всех значений аргумента.

Плотность распределения (или плотность вероятности) f(x) непрерывной случайной величины X в точке x характеризует плотность вероятности в окрестностях точки x и равна производной функции распределения этой СВ:

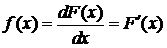. (6.1)

График плотности распределения называется кривой распределения.

Вероятность попадания случайной величины X на произвольный участок 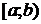равна сумме элементарных вероятностей на этом участке:

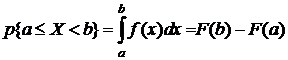. (6.2)

В геометрической интерпретации вероятность 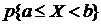равна площади, ограниченной сверху кривой распределения f(x) и отрезком .

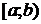Соотношение (6.2) позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

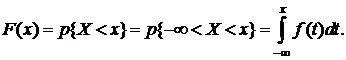(6.3)

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) 0. Причем f(x) = 0 для тех значений x, которые СВ никогда не принимает в опыте.

2. Условие нормировки:

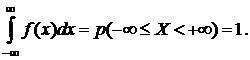(6.4)

Математическое ожидание характеризует среднее значение случайной величины и для непрерывной СВ определяется по формуле

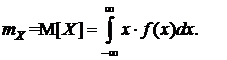(6.5)

Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для непрерывной СВ определяется по формуле

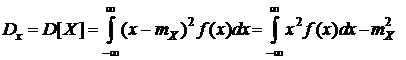. (6.6)

Дисперсия случайной величины имеет размерность квадрата случайной величины, поэтому для анализа диапазона значений величины Х дисперсия не совсем удобна. Этого недостатка лишено среднее квадратическое отклонение (СКО), размерность которого совпадает с размерностью случайной величины.

Среднее квадратическое отклонение случайной величины X характеризует ширину диапазона значений X и равно

Наши рекомендации