Множества. комбинаторика. графы и сети
ВАРИАНТ 1
1. Упростить, используя булевы тождества:
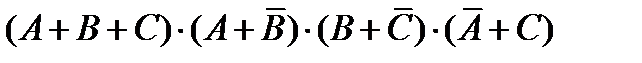
(после упрощения в формуле должно быть не менее трех букв).
2. Представить множество в виде суммы конституент:
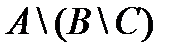 .
.
3. Справедливо ли следующее теоретико-множественное тождество:

4. Какое из отношений
1) 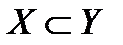 ; 2)
; 2) 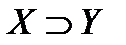 ; 3)
; 3) 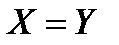 ; 4) никакое из указанных в 1)-3)
; 4) никакое из указанных в 1)-3)
имеет место для множеств 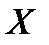 и
и 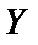 :
:
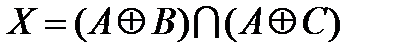 ,
, 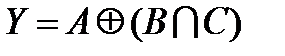 ?
?
5. Сколькими способами можно выбрать 12 человек из 17, если данные двое человек из этих 17 не могут быть выбраны вместе?
6. Сколькими способами можно переставить буквы слова «перешеек» так, чтобы четыре буквы «е» не шли подряд?
7. Шестеро студентов сдают экзамен. Сколькими способами могут быть поставлены им оценки, если известно, что никто из них не получил неудовлетворительной оценки?
8. Сколько можно построить различных четырехугольников, длина каждой стороны которых является целым числом от 1 до 5?
9. Найти 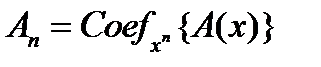 , где
, где 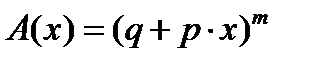 .
.
10. Найти решение линейного рекуррентного соотношения
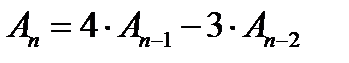 ;
; 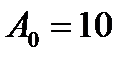 ,
, 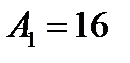 .
.
11. Выделить компоненты связности графа, заданного матрицей смежности 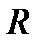 . Определить степени вершин и цикломатическое число графа.
. Определить степени вершин и цикломатическое число графа.
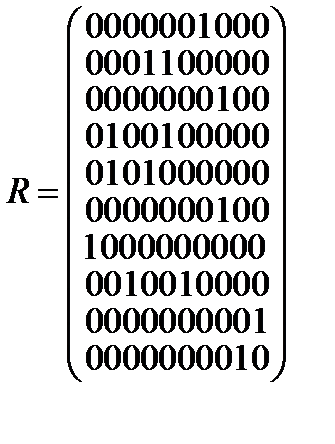 .
.
12. Найти диаметр, радиус и центры графа:








13. Построить кратчайшую цепь между вершинами 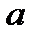 и
и 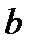 в ненагруженном графе:
в ненагруженном графе:
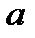




















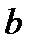
14. Построить кратчайшую цепь между вершинами 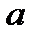 и
и 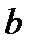 в нагруженном графе:
в нагруженном графе:


1 10 1 2 5
10  4
4  2
2
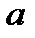
 6 4 1 5 8
6 4 1 5 8 
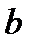
 3
3  5
5
3 2 6 3
 8
8 
15. Построить кратчайший остов для графа, заданного матрицей расстояний между его вершинами:
 .
.
16. Для данного графа построить две системы базисных циклов. Выразить циклы одной системы через циклы другой.





17. Построить максимальный поток в транспортной сети:
 10
10  12
12 
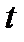
2 2 2 6
 1
1  4
4  6
6 
6 2 4 4
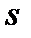
 14
14  10
10 
18. Определить словарный ранг матрицы:
 .
.
19. В сетевом графике найти критический путь, ранние и поздние сроки свершения событий, резервы времени и коэффициенты напряженности работ:
 5
5  3
3 
7 7 2
 5
5  10 4 9
10 4 9  7
7
3 1 5  12
12  15
15  конец
конец
2 5 5
 5
5  2
2  9
9 
 5
5 
начало 7 11 5 1 5
 3
3  11
11  5
5 
20. Построить сетевой график по заданной упорядоченности работ и определить критическое время выполнения всей совокупности работ:
| Работа | 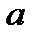 | 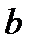 |  | 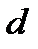 | 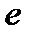 | 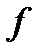 | 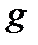 | 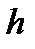 | 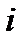 |
| Предшественники | 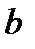 | – | 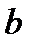 | 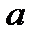 | 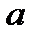 |  |  | 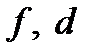 | 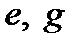 |
| Продолжительность |
ТИПОВОЙ РАСЧЕТ ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
МНОЖЕСТВА. КОМБИНАТОРИКА. ГРАФЫ И СЕТИ
ВАРИАНТ 2
1. Упростить, используя булевы тождества:
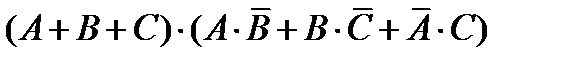
(после упрощения в формуле должно быть не менее трех букв).
2. Представить множество в виде суммы конституент:
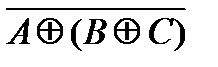 .
.
3. Справедливо ли следующее теоретико-множественное тождество:
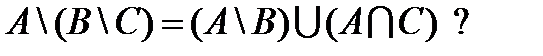
4. Какое из отношений
1) 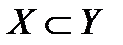 ; 2)
; 2) 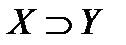 ; 3)
; 3) 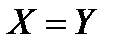 : 4) никакое из указанных в 1)-3)
: 4) никакое из указанных в 1)-3)
имеет место для множеств 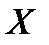 и
и 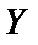 :
:
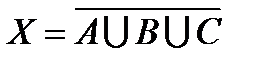 ,
, 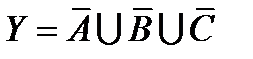 ?
?
5. Сколькими способами можно выбрать из слова «логарифм» две согласных и одну гласную букву?
6. Сколькими способами можно составить из 9 согласных и 7 гласных слова, в которые входят 4 различных согласных и 3 различных гласных?
7. Сколькими способами можно разложить 10 книг на 5 бандеролей по 2 книги в каждой?
8. Каково число матриц из 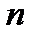 строк и
строк и 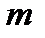 столбцов с элементами из множества
столбцов с элементами из множества
{0, 1}?
9. Найти 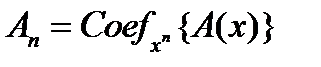 , где
, где 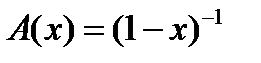 .
.
10. Найти решение линейного рекуррентного соотношения
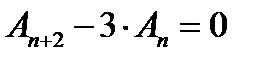 ;
; 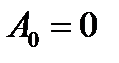 ,
, 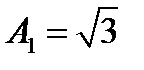 .
.
11. Выделить компоненты связности графа, заданного матрицей смежности 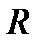 . Определить степени вершин и цикломатическое число графа.
. Определить степени вершин и цикломатическое число графа.
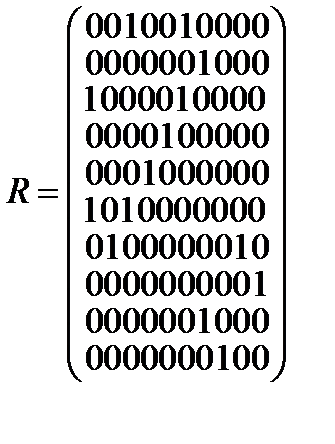 .
.
12. Найти диаметр, радиус и центры графа:









13. Построить кратчайшую цепь между вершинами 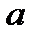 и
и 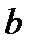 в ненагруженном графе:
в ненагруженном графе:
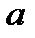




















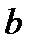
14. Построить кратчайшую цепь между вершинами 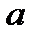 и
и 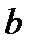 в нагруженном графе:
в нагруженном графе:
 1
1 
2 2 3 5 2
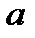
 5
5  1
1  6
6 
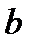
1 2 5 4 8
 2
2 
15. Построить кратчайший остов для графа, заданного матрицей расстояний между его вершинами:
 .
.
16. Для данного графа построить две системы базисных циклов. Выразить циклы одной системы через циклы другой.





17. Построить максимальный поток в транспортной сети:
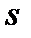
 15
15  12
12  4
4
7 3 7
 4
4  4
4  2
2 
6 6 3 8
 12
12  15
15 
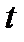
18. Определить словарный ранг матрицы:
 .
.
19. В сетевом графике найти критический путь, ранние и поздние сроки свершения событий, резервы времени и коэффициенты напряженности работ:
 7
7  3
3 
6 8 16
 5
5  6 12
6 12  16 4
16 4  8
8
6 4 5  12
12  15
15 
2 4 6 7
 7
7  2
2  4
4  7
7  5
5  5
5 

начало 4 10 9 3 4 конец
 8
8  7
7  4
4  6
6 
20. Построить сетевой график по заданной упорядоченности работ и определить критическое время выполнения всей совокупности работ:
| Работа | 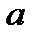 | 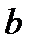 |  | 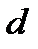 | 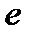 | 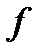 | 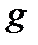 | 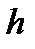 | 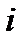 |
| Предшественники | – | – | 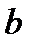 | 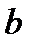 | 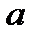 | 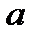 |  | 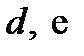 | 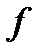 |
| Продолжительность |
