Проверка правильности расчета
Составим баланс мощностей. Если источник Е совпадает с током через него, то мощность данного источника записываем со знаком «+», если не совпадает – то со знаком «-».
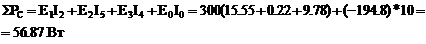
Е0 на зажимах источника тока определяем по второму закону Кирхгофа для контура содержащего источник тока, мысленно заменив I0 на Е0:
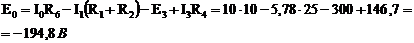
Мощности потребителей всегда положительны:
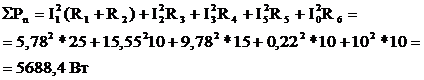5687 Вт ≈5688,4 Вт
Расхождение результатов правой и левой частей уравнения допускается не более 15%, в противном случае считается, что баланс мощностей не сошелся.
В нашем случае расхождение 0,02%.
Метод узловых и контурных уравнений
Метод применяется для расчета любых электрических цепей.
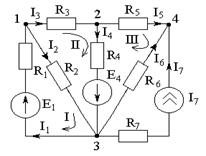 | Методика расчёта: 1) Произвольно задается направление токов в ветвях и направление обхода контуров. 2) Составляется система уравнений по законам Кирхгофа, причем число уравнений равно числу неизвестных токов (ветвей). а) По I-му закону Кирхгофа записываются узловые уравнения, причем их число равно числу узлов в схеме “-1” (1) Узел “1” I1=I3+I2 (2) Узел “2” I3=I4+I5 (3) Узел “3” I2+I4=I1+I6+I7 n — число узлов в схеме n – 1= 4 – 1=3 уравнения |
б) По II-му закону Кирхгофа записываются контурные уравнения, причем их число рассчитывается по формуле: m – (n – 1),
где m — число неизвестных токов (ветвей).
| Контур I: | Контур II: | Контур III: |
| E1=I1R1+I2R2 (4) | E4=I3R3+I4R4–I2R2 (5) | –E4=I5R5–I6R6–I4R4 (6) |
3) Решаем систему любым известным из математики способом и находим неизвестные токи.
Вывод: Если в результате расчета какие-либо токи получатся отрицательными, значит направление этих токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание — для контура, содержащего источник тока, уравнение по II-му закону Кирхгофа не записывается.
Пример решения:
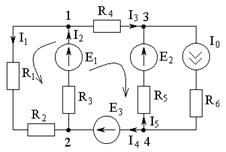 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Задаем направления токов в ветвях схемы.
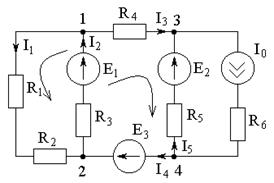
2. По законам Кирхгофа составляем систему уравнений, причем по первому закону (в схеме 4 узла): 4-1=3 уравнения, по второму закону (в схеме 6 неизвестных токов) 6-(4-1)=3 уравнения. Всего 6 уравнений (в одной ветке стоит источник тока, ток данной ветки уже известен) остается 5 уравнений:
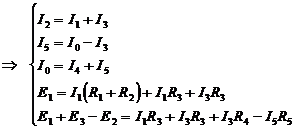
Решим систему методом подстановки:
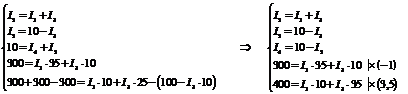
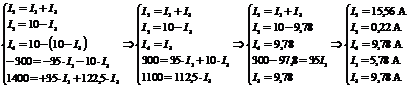
В результате расчета все токи получились положительные, значит их направление выбрано, верно. Значения токов совпали со значениями предыдущих токов.
Решение верно.
Метод узловых потенциалов
Метод позволяет сократить число уравнений в системе до n–1 (n—количество узлов).
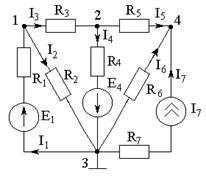 | Узловым напряжением называется разность потенциалов между данным узлом и базисным (jк-го=0). По I-му закону Кирхгофа для независимых узлов (1,2,4):  |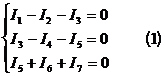
По обобщенному закону Ома токи в ветвях:
Для “1” узла: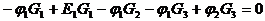 
Перепишем систему уравнений (1):
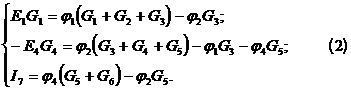
Методика расчета:
1) Произвольно задаются направления I-ов в ветвях.
2) Намечается базисный узел (j=0) и все независимые узлы.
3) Составляется система уравнений для независимых узлов типа :
в левой части уравнения — S произведений Е ветвей, сходящихся в данном узле, на соответствующие им проводимости и S источников тока;
в правой части уравнения — произведение j рассматриваемого узла и суммы проводимостей ветвей, сходящихся в данном узле, минус j противоположных концов этих ветвей, умноженных на проводимости этих ветвей.
4) ЭДС (I0) учитывается со знаком “+”, если направлена в данный узел, и наоборот.
5) Решаем систему уравнений любым известным из математики способом.
6) Определяем токи в ветвях по обобщенному закону Ома.
Вывод : Если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание — если в схеме есть ветвь с чистой Е (без R), то в качестве нулевого j необходимо взять один из узлов данной ветви, а ток ветви рассчитывается по I-му закону Кирхгофа.
Частный случай: Метод 2-х узлов.
Можно применять в схемах, имеющих любое количество активных или пассивных ветвей, но только два узла.
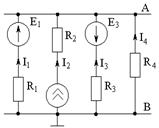 | Методика расчета : 1) Направление токов в ветвях задается произвольно, но к одному узлу. 2) Записывается уравнение узлового U, причем ЭДС считается “+”, если направление I и Е ветви совпадают, и наоборот :  |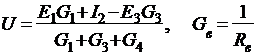
3) Определяются токи ветвей по формуле:
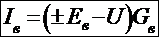
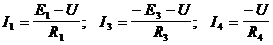
Е считается “+”, если направлениеЕ и I ветви совпадают.
Вывод и проверка — см. Выше.
1) ЕслиЕ ветви> U, то источник работает в режиме генератора.
2) Если Е ветви< U, то источник работает в режиме потребителя.
3) Если Е ветви = U, то источник работает в режиме Х.Х. и её можно включить и отключить не нарушая рабочего режима работы.
4) Если в ветви только чистая Е, то U=Ев и нет необходимости рассчитывать U между узлами.
Пример решения:
| | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Задаем направления токов в ветвях.
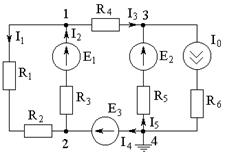
2. Задаем базисный узел (φ4=0), так как он принадлежит к ветке с чистой Е3 (без резистора), остальные узлы соответственно с потенциалами φ1, φ2, φ3.
Тогда φ1=Е3=300 В.
3. Составляем систему уравнений для независимых узлов (2,3):
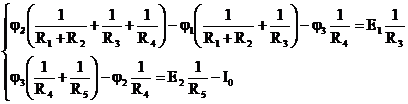
Решим систему методом подстановки:
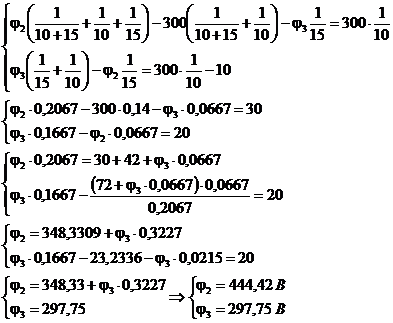
4. По обобщенному закону Ома находим токи в ветвях схемы. Ток ветви прямо пропорционален разности потенциалов концов ветви, по которой протекает ток (ток течет от большего потенциала к меньшему) и ЭДС ветви («+» - если ЭДС совпадает по направлению с током) и обратно пропорционален сопротивлению ветви.
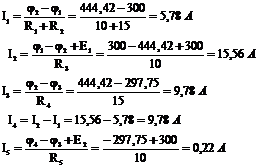
В результате расчета все токи получились положительные, значит их направление выбрано верно. Значения токов совпали со значениями предыдущих токов.
Решение верно.
Метод контурных токов
Метод позволяет уменьшить число уравнений до (m-n+1).
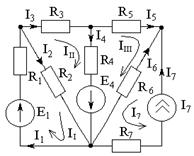 | Методика расчета: 1) Произвольно задаются направления токов в ветвях. 2) Произвольно задаются направления контурных токов в независимых контурах схемы. Контурный ток — расчетная величина, которая одинакова для всех ветвей данного контура. Контурный ток равен действительному току ветви, которая принадлежит только данному контуру. |
3) Составляются уравнения для определения действительных токов:
для смежных ветвей — наложением контурных токов, соответствующих смежных контуров;
для независимых ветвей — если контурный ток совпадает с направлением I ветви, то Iв=Iк, если не совпадает, то Iв= –Iк.
I1=II; I3=III; I5=IIII — для независимых ветвей;
I2=II–III; I4=III–IIII; I6=–IIII–I7 — для ветвей смежных контуров.
4) По II-му закону Кирхгофа составляются контурные уравнения:
ЭДС считается положительной, если направления ЭДС и контурного тока совпадают и наоборот;
падение напряжения от собственного контурного тока всегда “+”;
падение напряжения от смежного контура в ветви их соприкосновения будет “+”, если направления контурных токов в ветви соприкосновения смежных контуров совпадают и наоборот.
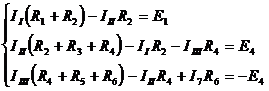
5) Полученная система решается любым известным из математики способом, и определяются величины контурных токов.
6) По уравнениям п.3 определяются реальные токи.
Вывод: Если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание: Для контура, содержащего источник тока, уравнение по II-му закону Кирхгофа не записывается, но падение напряжения в смежном контуре от данного контура учитывается на общих основаниях (см. уравнение 3 п.4)
Пример решения:
| | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Задаем направления токов в ветвях.
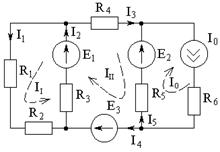
2. Задаем направление контурных токов в независимых контурах схемы (II, III, I0).
3. По второму закону Кирхгофа составляем контурные уравнения для контуров с токами II и III.
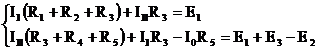
Для контура I0 уравнение не составляется, так как он содержит источник тока.
Решим систему методом подстановки.
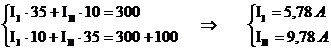
4. Определяем действительные токи ветвей.
- для независимых ветвей:
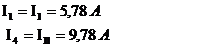
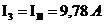
- для ветвей смежных контуров:
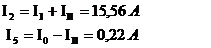
В результате расчета все токи получились положительные, значит их направление выбрано верно. Значения токов совпали со значениями предыдущих токов.
Решение верно.