Минимизация функции q2 выхода ОЧУС с помощью алгоритма рота
· Исходные данные :
L-Кубы:000011, 000100, 001010, 001011, 010011, 011010, 011011, 011100, 100100, 111100
N-Кубы:xxx11x, 1xxxx1, 1xx0xx
· Этап поиска простыхимпликант:
| C0*C0 | xxx11x | 1xx0xx | 1xxxx1 | ||||||||||
| - | |||||||||||||
| 000yyy | - | ||||||||||||
| 00y01y | 00yyy0 | - | |||||||||||
| 00y011 | 00yyyy | 00101y | - | ||||||||||
| 0y0011 | 0y0yyy | 0yy01y | 0yy011 | - | |||||||||
| 0yy01y | 0yyyy0 | 0y1010 | 0y101y | 01y01y | - | ||||||||
| 0yy011 | 0yyyyy | 0y101y | 0y1011 | 01y011 | 01101y | - | |||||||
| 0yyyyy | 0yy100 | 0y1yy0 | 0y1yyy | 01yyyy | 011yy0 | 011yyy | - | ||||||
| y00yyy | y00100 | y0yyy0 | y0yyyy | yy0yyy | yyyyy0 | yyyyyy | yyy100 | - | |||||
| yyyyyy | yyy100 | yy1yy0 | yy1yyy | y1yyyy | y11yy0 | y11yyy | y11100 | 1yy100 | - | ||||
| xxx11x | 000y11 | 0001y0 | 001y10 | 001y11 | 010y11 | 011y10 | 011y11 | 0111y0 | 1001y0 | 1111y0 | - | ||
| 1xx0xx | y00011 | y00y00 | y01010 | y01011 | y10011 | y11010 | y11011 | y11y00 | 100y00 | 111y00 | 1xxy1x | - | |
| 1xxxx1 | y00011 | y0010y | y0101y | y01011 | y10011 | y1101y | y11011 | y1110y | 10010y | 11110y | 1xx111 | 1xx0x1 | - |
| A1 | 00x011 | x00100 | 00101x | 0x1011 | 01x011 | 01101x | 011x11 | x11100 | 1001x0 | 1111x0 | 1xxx1x | Ø | Ø |
| 0x0011 | |||||||||||||
| 000x11 | 0x1010 | 001x11 | 010x11 | 011x10 | x11011 | 100x00 | 111x00 | ||||||
| x00011 | 0001x0 | 001x10 | x01011 | x10011 | x11010 | x11011 | 0111x0 | 10010x | 11110x | ||||
| x00011 | x01010 | x01011 | x10011 |
Получаем:
A1 = {00x011; 0x0011; 000x11; x00011; x00100; 0001x0; 00101x; 0x1010; 001x10; x01010; 0x1011; 001x11; x01011; 01x011; 010x11; x10011; 01101x; 011x10; x11010; 011x11; x11011; x11100; 0111x0; 1001x0; 100x00; 10010x; 1111x0; 111x00; 11110x; 1xxx1x }
Z1 = { Ø }
B1 = { 000011; 000100; 001010; 001011; 010011; 011010; 011011; 011100; 100100; 111100; xxx11x; 1xx0xx; 1xxxx1 }
C1 = { 00x011; 0x0011; 000x11; x00011; x00100; 0001x0; 00101x; 0x1010; 001x10; x01010; 0x1011; 001x11; x01011; 01x011; 010x11; x10011; 01101x; 011x10; x11010; 011x11; x11011; x11100; 0111x0; 1001x0; 100x00; 10010x; 1111x0; 111x00; 11110x; 1xxx1x; xxx11x; 1xx0xx; 1xxxx1 }
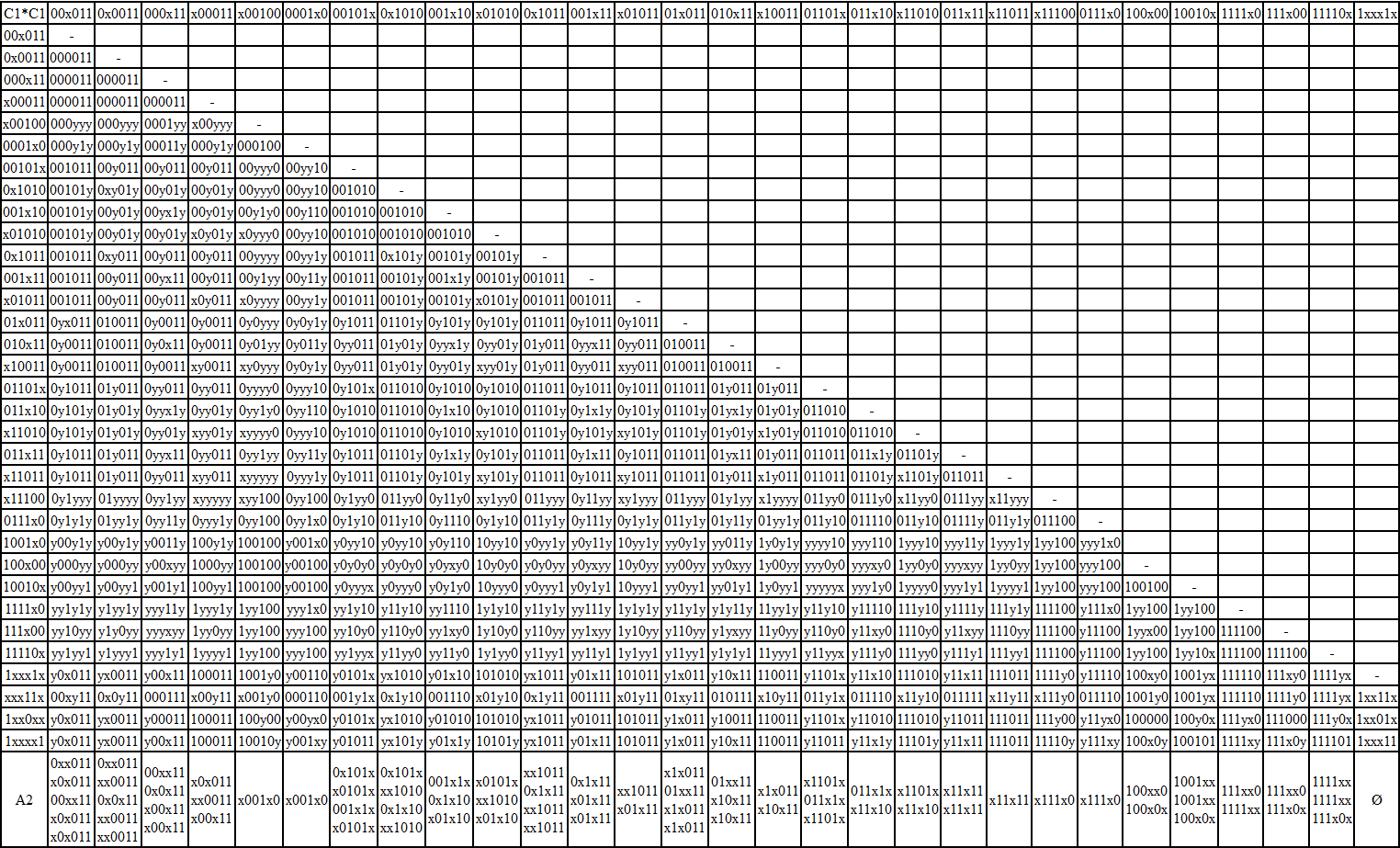
Получаем:
A2 = { 0xx011; x0x011; 00xx11; xx0011; 0x0x11; x00x11; x001x0; 0x101x; x0101x; 001x1x; xx1010; 0x1x10; x01x10; xx1011; 0x1x11; x01x11; x1x011; 01xx11; x10x11; x1101x; 011x1x; x11x10; x11x11; x111x0; 100xx0; 1001xx; 100x0x; 111xx0; 1111xx; 111x0x }
Z1 = { Ø }
B2 = { 00x011; 0x0011; 000x11; x00011; x00100; 0001x0; 00101x; 0x1010; 001x10; x01010; 0x1011; 001x11; x01011; 01x011; 010x11; x10011; 01101x; 011x10; x11010; 011x11; x11011; x11100; 0111x0; 1001x0; 100x00; 10010x; 1111x0; 111x00; 11110x; 1xxx1x; xxx11x; 1xx0xx; 1xxxx1 }
C2 = { 0xx011; x0x011; 00xx11; xx0011; 0x0x11; x00x11; x001x0; 0x101x; x0101x; 001x1x; xx1010; 0x1x10; x01x10; xx1011; 0x1x11; x01x11; x1x011; 01xx11; x10x11; x1101x; 011x1x; x11x10; x11x11; x111x0; 100xx0; 1001xx; 100x0x; 111xx0; 1111xx; 111x0x; 1xxx1x; xxx11x; 1xx0xx; 1xxxx1 }
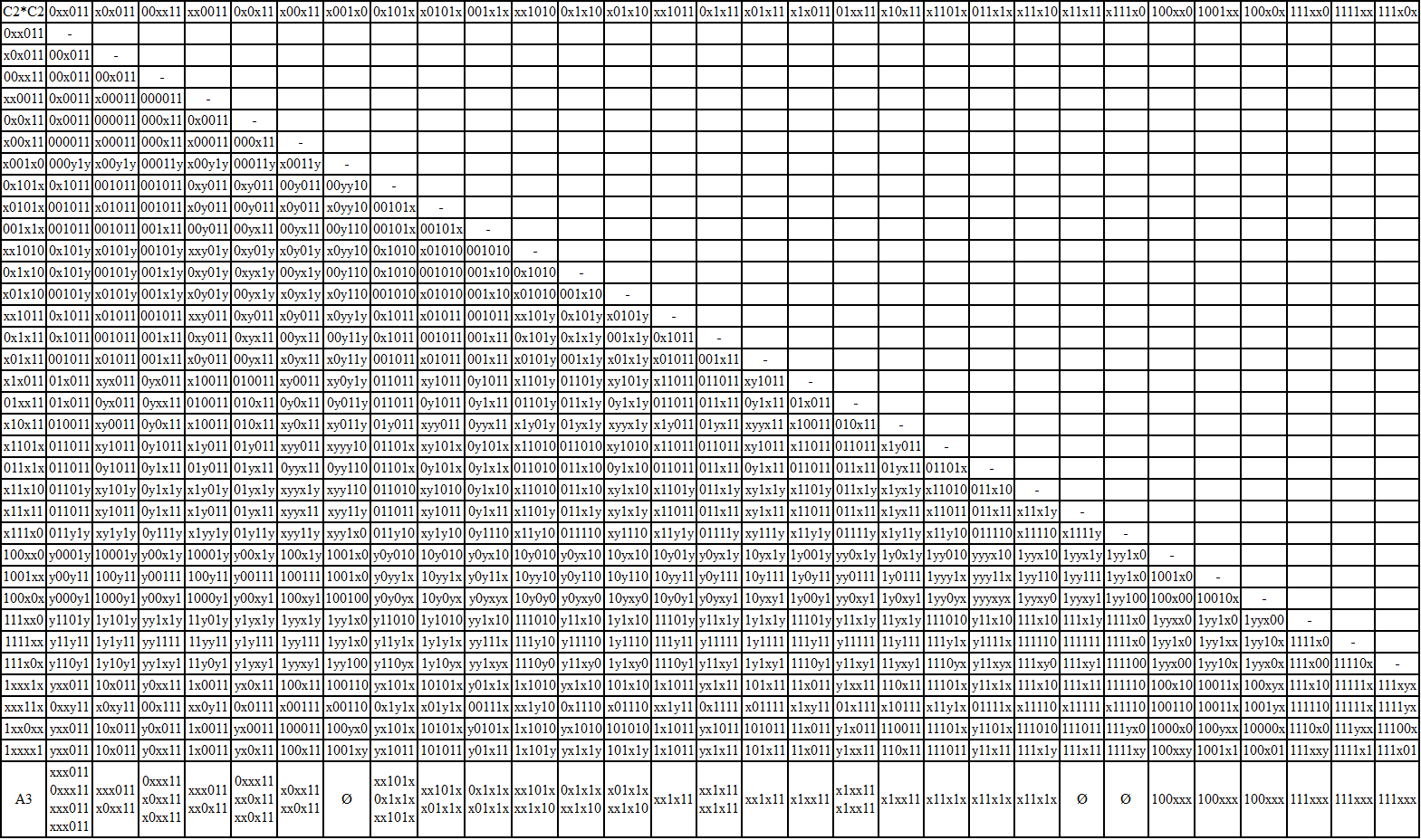
Получаем:
A3 = { xxx011; 0xxx11; x0xx11; xx0x11; xx101x; 0x1x1x; x01x1x; xx1x10; xx1x11; x1xx11; x11x1x; 100xxx; 111xxx }
Z2 = {x001x0; x111x0 }
B3 = {0xx011; x0x011; 00xx11; xx0011; 0x0x11; x00x11; 0x101x; x0101x; 001x1x; xx1010; 0x1x10; x01x10; xx1011; 0x1x11; x01x11; x1x011; 01xx11; x10x11; x1101x; 011x1x; x11x10; x11x11; 100xx0; 1001xx; 100x0x; 111xx0; 1111xx; 111x0x; 1xxx1x; xxx11x; 1xx0xx; 1xxxx1 }
| C3*C3 | xxx011 | 0xxx11 | x0xx11 | xx0x11 | xx101x | 0x1x1x | x01x1x | xx1x10 | xx1x11 | x1xx11 | x11x1x | 100xxx | 111xxx |
| xxx011 | - | ||||||||||||
| 0xxx11 | 0xx011 | - | |||||||||||
| x0xx11 | x0x011 | 00xx11 | - | ||||||||||
| xx0x11 | xx0011 | 0x0x11 | x00x11 | - | |||||||||
| xx101x | xx1011 | 0x1011 | x01011 | xxy011 | - | ||||||||
| 0x1x1x | 0x1011 | 0x1x11 | 001x11 | 0xyx11 | 0x101x | - | |||||||
| x01x1x | x01011 | 001x11 | x01x11 | x0yx11 | x0101x | 001x1x | - | ||||||
| xx1x10 | xx101y | 0x1x1y | x01x1y | xxyx1y | xx1010 | 0x1x10 | x01x10 | - | |||||
| xx1x11 | xx1011 | 0x1x11 | x01x11 | xxyx11 | xx1011 | 0x1x11 | x01x11 | xx1x1y | - | ||||
| x1xx11 | x1x011 | 01xx11 | xyxx11 | x10x11 | x11011 | 011x11 | xy1x11 | x11x1y | x11x11 | - | |||
| x11x1x | x11011 | 011x11 | xy1x11 | x1yx11 | x1101x | 011x1x | xy1x1x | x11x10 | x11x11 | x11x11 | - | ||
| 100xxx | y00x11 | 100x11 | 100x11 | 10y01x | y0yx1x | 10yx1x | 10yx10 | 10yx11 | 1y0x11 | 1yyx1x | - | ||
| 111xxx | y11x11 | 1y1x11 | 11yx11 | 11101x | y11x1x | 1y1x1x | 111x10 | 111x11 | 111x11 | 111x1x | 1yyxxx | - | |
| 1xxx1x | 1xx011 | yxxx11 | 10xx11 | 1x0x11 | 1x101x | yx1x1x | 101x1x | 1x1x10 | 1x1x11 | 11xx11 | 111x1x | 100x1x | 111x1x |
| xxx11x | xxxy11 | 0xx111 | x0x111 | xx0111 | xx1y1x | 0x111x | x0111x | xx1110 | xx1111 | x1x111 | x1111x | 10011x | 11111x |
| 1xx0xx | 1xx011 | yxx011 | 10x011 | 1x0011 | 1x101x | yx101x | 10101x | 1x1010 | 1x1011 | 11x011 | 11101x | 1000xx | 1110xx |
| 1xxxx1 | 1xx011 | yxxx11 | 10xx11 | 1x0x11 | 1x1011 | yx1x11 | 101x11 | 1x1x1y | 1x1x11 | 11xx11 | 111x11 | 100xx1 | 111xx1 |
| A4 | xxxx11 | xxxx11 | xxxx11 | xxxx11 | xx1x1x | xx1x1x | xx1x1x | xx1x1x | Ø | Ø | Ø | Ø | Ø |
C3 = {xxx011; 0xxx11; x0xx11; xx0x11; xx101x; 0x1x1x; x01x1x; xx1x10; xx1x11; x1xx11; x11x1x; 100xxx; 111xxx; 1xxx1x; xxx11x; 1xx0xx; 1xxxx1 }
Получаем:
A4 = { xxxx11; xx1x1x }
Z3 = {x001x0; x111x0; 100xxx; 111xxx; 1xx0x }
B4 = {xxx011; 0xxx11; x0xx11; xx0x11; xx101x; 0x1x1x; x01x1x; xx1x10; xx1x11; x1xx11; x11x1x; 1xxx1x; xxx11x; 1xxxx1 }
C4 = {xxxx11; xx1x1x; 1xxx1x; xxx11x; 1xxxx1 }
| C4*C4 | xx10xx | xx1x1x |
| xxxx11 | - | |
| xx1x1x | xx1x11 | - |
| 1xxx1x | 1xxx11 | 1x1x1x |
| xxx11x | xxx111 | xx111x |
| 1xxxx1 | 1xxx11 | 1x1x11 |
| A5 | Ø | Ø |
В результате:
так как |С5|£1, то поиск простых импликант закончен
Множество простыхимпликант:Z = {x001x0; x111x0; 100xxx; 111xxx; 1xx0xx; xxxx11; xx1x1x; 1xxx1x; xxx11x; 1xxxx1 }
Этап поиска простыхимпликант:
На этом этапе необходимо проверить нет ли среди кубов таких, которые стали L-экстремалями за счет безразличных. Для этого из кубов множества L вычитаются остатки простых импликант, выполняем операцию решетчатого вычитания- из каждой простой импликанты поочередно вычитаются все прочие простые импликанты Z#(Z\z)
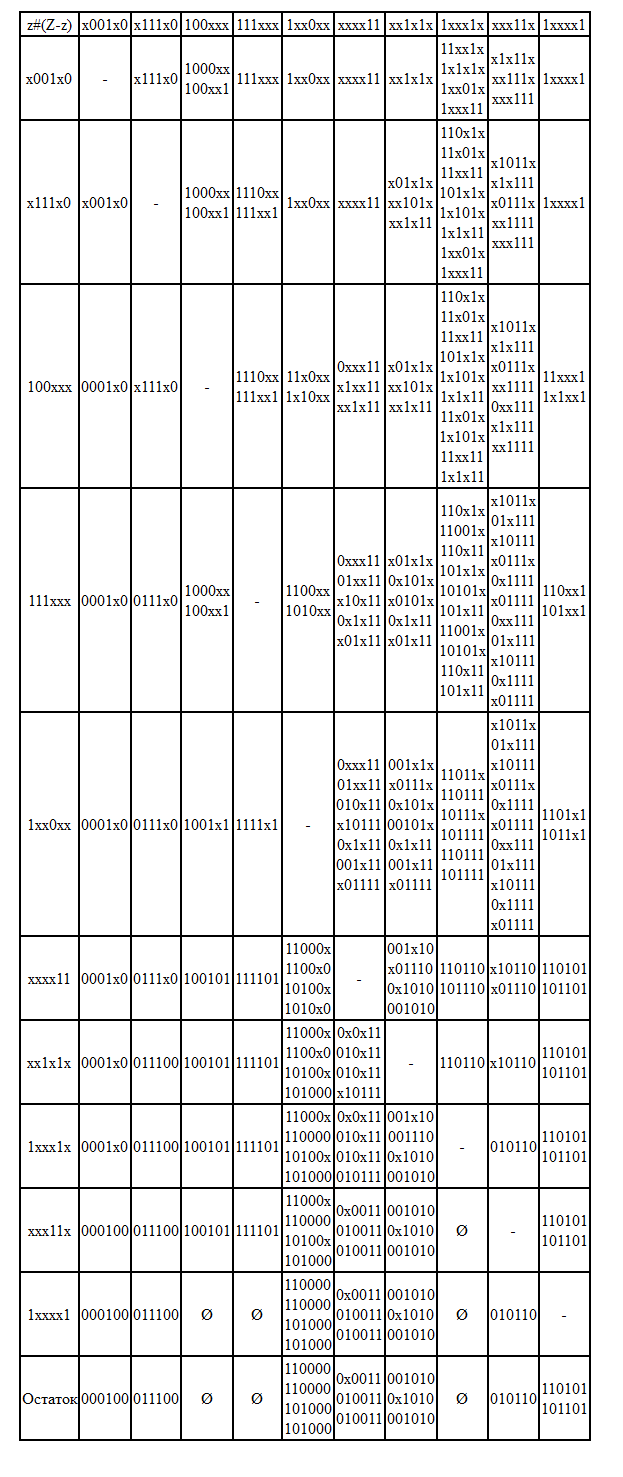
z#(Z-z) 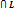 | ||||||||||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| 0x0011 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x1010 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | |
| Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Проверка L-экстремалей
Множество L-экстремалей E ={x001x0; x111x0; xxxx11; xx1x1x }
Z´ = Z - E ={100xxx; 111xxx; 1xx0xx; 1xxx1x; xxx11x; 1xxxx1 }
Проверка покрытия множества Z´ множеством найденных L-экстремалей Е
| L#E | ||||||||||
| x001x0 | Ø | Ø | ||||||||
| x111x0 | Ø | Ø | Ø | Ø | ||||||
| xxxx11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| xx1x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| Остаток | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Конечное минимальное множество= { x001x0; x111x0; xxxx11; xx1x1x }
