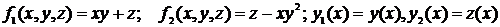Тема 4. Численные методы решения обыкновенных дифференциальных уравнений

ОДУ порядка n называется уравнение вида

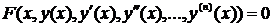(4.1)

где n - порядок наивысшей производной, входящей в уравнение.

Примеры дифференциальных уравнений:

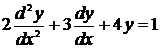(4.2)

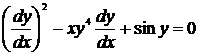(4.3)

Здесь y(x) – неизвестная функция.

Уравнение (4.2) имеет порядок 2, уравнение (4.3) – порядок 1.

Если уравнение линейно по 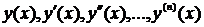, то оно называется линейным. (4.2) – линейное уравнение, (4.3) – нелинейное.

Запишем дифференциальное уравнение n порядка в явном виде:

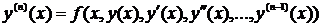(4.4)

Уравнение в виде (4.1) – уравнение в неявной форме.

Под интегрированием уравнения (4.1) понимают нахождение функции y(x), которая удовлетворяет этому уравнению. y(x) называется решением дифференциального уравнения. Общее решение ОДУ n -го порядка имеет вид:

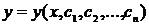(4.5)

где 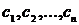- произвольные константы.

При любом наборе конкретных констант получаются частные решения.

Задача Коши есть задача о нахождении частного решения уравнения (4.4), удовлетворяющего начальным условиям

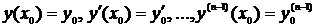(4.6)

Здесь 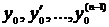- некоторые заданные числа.

Графическое изображение частного решения называют интегральной кривой. Общее решение дифференциального уравнения n-го порядка определяет n-параметрическое семейство интегральных кривых.

Задача Коши для обыкновенного дифференциального уравнения 1-го порядка

Рассмотрим два численных метода решения ОДУ первого порядка. Пусть дифференциальное уравнение первого порядка задано в виде

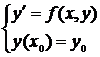(4.7)

Задача (4.7) – задача Коши для ОДУ первого порядка.

Пример:

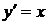Общее решение этого уравнения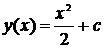

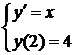
Решением этой задачи Коши будет единственная функция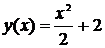

Так решались ДУ в курсе высшей математики.

Метод Эйлера

Перепишем уравнение (4.7) в виде

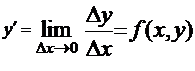
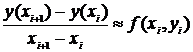Обозначим 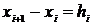. Тогда

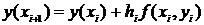(4.8)

Формула (4.8) – формула метода Эйлера решения ОДУ первого порядка.

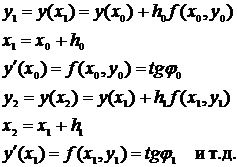
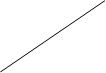
Y *

*

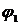
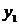
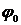
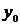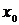
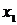
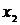X

Результатом численного решения дифференциального уравнения является таблица

X				…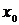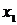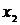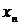
Y				…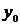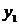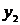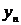

где 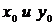заданы, 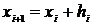(шаг h_i задается и может быть как переменным, так и постоянным, а y_i (i=1, 2, … , n) вычисляются по соответствующим формулам (например, по формуле (4.8)).

Пример:

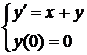h=0.2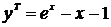

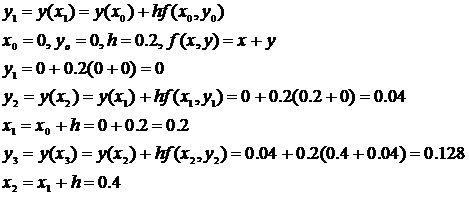
x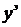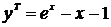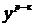
0.2		0.021403	0.0214
0.4	0.04	0.091825
0.6	0.128	0.222119

Погрешность метода Эйлера – o(h).

Метод Рунге-Кутта решения ОДУ первого порядка

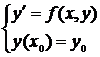
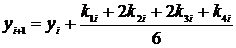
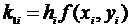
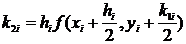
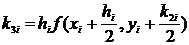
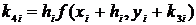
Погрешность метода Рунге-Кутта – o(h⁴).

Пример:

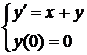h=0.2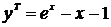

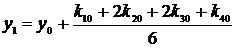
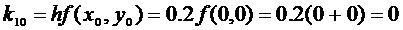
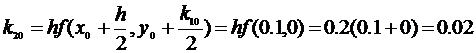
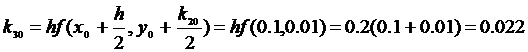
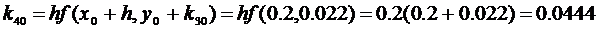
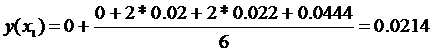
Решение систем дифференциальных уравнений первого порядка

Запишем систему дифференциальных уравнений первого порядка:

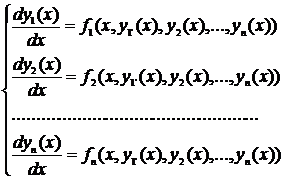(4.10)

Здесь x – независимая переменная, f₁, f₂, …, f_n – заданные функции.

Решением (4.10) называют совокупность функций 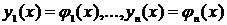, которые после подстановки в систему уравнений (4.10) обращают их в тождество.

Задача Коши для системы (4.10) ставится так:

Найти 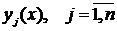такие, что 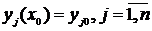, 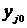- некоторые заданные числа.

Метод Эйлера для решения задачи Коши заключается в вычислении 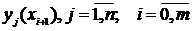по формулам:

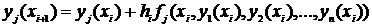(4.11)

Пример:

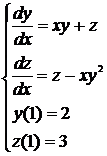Формулы для вычислений будут такими:

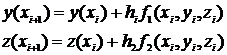
Здесь