Синтез комбинационных схем устройств умножения на основе мультиплексоров

Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2^m.

Принцип работы мультиплексора состоит в следующем. На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.

На рис. 9 показан мультиплексор, имеющий 4 информационных (I0–I3) и два управляющих (S0, S1) входа, так называемый ”один из четырех”. В табл. 14 определена зависимость выходного сигала Y от сигналов на входах мультилексора. Сигналы х₁, x₂, x₃, x₄ - это логические сигналы, поступающие на вход мультиплексора, которые могут принимать значения ноль или единица.

Из табл. 14 видно, что под действием управляющей комбинации S0S1 на выход будет пропущен сигнал, поданный на вход I0 (в нашем случае это х₁), а управляющая комбинация S0S1 пропускает на выход сигнал, поданный на вход I2 (в нашем случае это х₃).

	I0	MS	Y			Работа мультиплексора. Таблица 14.
		S0	S1	I0	I1	I2	I3	Y
I1				x1	x2	x3	x4	x1
				x1	x2	x3	x4	x2
I2				x1	x2	x3	x4	x3
				x1	x2	x3	x4	x4
I3
S0
S1
Рис.9. Мультиплексор

Мультиплексор может быть использован для синтеза комбинационных схем. С помощью мультиплексора ”один из четырех” легко реализовать любую переключательную функцию (ПФ) от двух переменных. Пример реализации функций ИЛИ и И на мультиплексоре по таблицам истинности 15 и 16 приведен соответственно на рис. 10 и 11.

Функция ”ИЛИ”. Таблица 15.

x1

x2

x1Åx2

“0”

I0

MS

Y

y = x1Åx2

“1”

I1

I2

I3

x1

S0

x2

S1

Рис.10. Реализация функции ”ИЛИ” на мультиплексоре

Функция ”И”. Таблица 16.

x1

x2

x1·x2

“0”

I0

MS

Y

y = x1·x2

I1

I2

“1”

I3

x1

S0

x2

S1

Рис.11. Реализация функции ”И” на мультиплексоре

На основе мультиплексора можно синтезировать ПФ более чем от двух переменных. Для этого на входе мультиплексора, возможно, придется разместить некоторую дополнительную логическую схему. Для синтеза этой дополнительной схемы все наборы в таблице истинности (табл. 17) целесообразно поделить на группы так, чтобы в каждой группе наборы переменных х₁, х₂ были одинаковы. Таких групп с одинаковыми наборами 00, 01, 10, 11 будет четыре.

Для синтеза входной логической схемы независимыми переменными будут только х₃ и х₄, которые в свою очередь образуют четыре различных набора в каждой группе. Записывая для единичных значений ПФ логические выражения для входных переменных х₃ и х₄, строим затем по этим выражениям для каждого входа I0 – I3 логическую схему. Например, для первой и четвертой групп y=x₃x₄+x₃x₄ = x₃ Å x₄ , а для второй и третьей групп y = 1, поскольку ПФ на всех восьми наборах равна 1.

Мультиплексор с входной логической схемой для реализации ПФ четырех переменных показан на рис. 12.

Переключательные функции пяти переменных можно реализовать на мультиплексоре “один из восьми”, применяя аналогичный подход. Здесь управляющее поле определяется тремя переменными х₁, х₂, х₃, поэтому число групп с одинаковыми значениями этих переменных будет равно восьми (табл. 18). Заметим еще раз, что каждая такая группа управляет одним из восьми входов I0 – I7_.

Таблица истинности. Таблица 18.
	x1	x2	x3	x4	x5	y
.	.	.	.	.	.	.

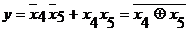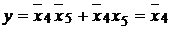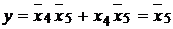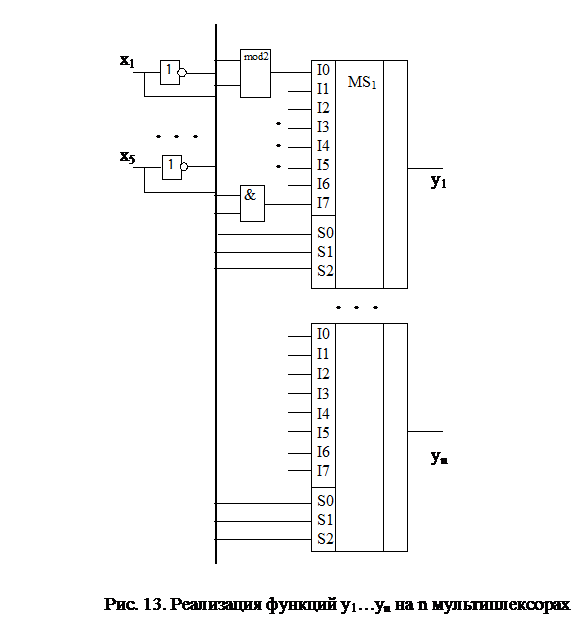
Входная логическая схема синтезируется только для входных переменных x₄ и x₅ исходя из заданных единичных значений ПФ, оказавшихся в той или иной группе. Например, для нулевой группы ; для первой группы и т.д., а для седьмой и восьмой групп и 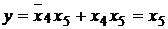. Реализация нескольких ПФ, как например ОЧС, потребует для каждой ПФ отдельного мультиплексора (рис. 13).

Литература

1. Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высшая школа, 1985.

2. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. Мн.: Вышейшая школа, 1980.

3. Лысиков Б.Г. Цифровая вычислительная техника. Мн.: , 2003 г.

4. Луцик Ю.А., Лукьянова И.В., Ожигина М.П. – Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ ,2001 г.

5. Луцик Ю.А., Лукьянова И.В.– Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ ,2004 г.

ПРИЛОЖЕНИЕ

Таблица П1. Исходные данные к расчетной работе

№вар.

Сомножители в десятичной системе счисления

Мн

43,34

81,92

65,91

15,44

36,39

48,51

68,39

28,69

73,48

49,27

72,34

67,83

56,59

29,63

52,26

48,27

84,19

16,35

31,50

72, 95

37, 32

28, 12

78, 11

42, 97

Мт

32,65

44,35

17,39

47,31

53,25

69,11

16,71

21,59

49,13

38,70

35,44

25,37

18,27

63,29

83,31

72,23

55,13

67,21

45,17

67, 65

28, 15

69, 97

25, 17

55, 39

Алгоритм выполнения операции умножения

А

Б

В

Г

А

Б

В

Г

А

Б

В

Г

А

Б

В

Г

А

Б

В

Г

А

Б

В

Г

Варианты кодирования четверичных цифр двоичными кодами

“0”

“1”

“2”

“3”

Логический базис для реализации ОЧС (см. табл.2) и метод минимизации.

А1

А2

А3

А4

А5

А6

А7

А1

А2

А3

А4

А5

А6

А7

А1

А2

А3

А4

А5

А6

А7

А1

А2

А3

Карты Карно-Вейча

Алгоритм Рота

Логический базис для реализации ОЧУ(ОЧУС, см. табл.2) и метод минимизации.

А4

А5

А6

А7

А1

А2

А3

А4

А5

А6

А7

А1

А2

А3

А4

А5

А6

А7

А1

А2

А3

А4

А5

А6

Алгоритм Рота

Карты Карно-Вейча

Тип реализуемой структурной схемы

Таблица П2 Логический базис для реализации схем

Функционально полный Логический базис	Базовые логические Элементы
& А1	x х1х2 х1 + х2
A2	х1х2 x1Åx2	&     “1” mod2
A3	х1+х2 x1Åx2	“1”     mod2
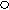А4	х1х2 _ Х	&
А5	х1+х2 _ Х
А6	х1х2	&
А7	х1+х2

Содержание

Задание к расчетной работе. 3

Исходные данные к расчетной работе. 4

Пример синтеза сумматора-умножителя (разработка алгоритма умножения и структурной схемы сумматора-умножителя) 5

Разработка алгоритма умножения. 5

Разработка структурной схемы сумматора-умножителя. 1

Синтез структуры сумматора-умножителя 1-го типа. 2

Синтез структуры сумматора-умножителя 2-го типа. 2

Разработка функциональных схем основных узлов сумматора-умножителя. 4

Логический синтез одноразрядного четверичного умножителя. 4

Логический синтез одноразрядного четверичного сумматора. 6

Логический синтез одноразрядного четверичного умножителя-сумматора. 13

Синтез комбинационных схем устройств умножения на основе мультиплексоров 16

Литература. 21

ПРИЛОЖЕНИЕ. 23

Таблица П1. Исходные данные к расчетной работе. 23

Таблица П2 Логический базис для реализации схем. 25

Св. план , поз.

УЧЕБНОЕ ИЗДАНИЕ

МЕТОДИЧЕСКОЕ ПОСОБИЕ

к расчетной работе

по курсу