Арифметические и логические основы
АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
для студентов специальности
”Вычислительные машины, системы и сети”
всех форм обучения
Минск 2006
УДК 004.7 (075.8)
ББК 32.97 я 73
Л 84
Лукьянова И.В., Луцик Ю.А.
| Л 84 | Арифметические и логические основы вычислительной техники: Методические пособие к расчетной работе / Ю.А. Луцик, И.В. Лукъянова, − Мн.: БГУИР, 2006. − с.: ил. . ISBN 985-444-642-5 |
| В методическом пособии приведены исходные данные для выполнения расчетной работы и рассмотрен пример выполнения и оформления расчетной работы для одного из вариантов задания. Пособие может быть использовано студентами всех форм обучения, специальности 40 02 01 ”Вычислительные машины системы и сети”, магистрантами и аспирантами. |
УДК 004.7 (075.8)
ББК 32.97 я 73
© Лукьянова И.В., Луцик Ю.А., 2006
ISBN 985-444-642-5 © БГУИР, 2006
Задание к расчетной работе
Расчетная работа предполагает синтез цифровых схем арифметических устройств, выполняющих операции сложения и умножения над числами, представленными в форме с плавающей запятой в двоичной и двоично-четверичной системах счисления (с/с).
По исходным данным необходимо разработать:
1. Алгоритм выполнения операции умножения, для чего потребуется:
§ перевести заданные исходные числа в четверичную систему счисления;
§ представить числа в форме с плавающей запятой, при этом число четверичных разрядов для мантиссы равно шести, для порядка – два, плюс два разряда для знаков мантиссы и порядка;
§ произвести перемножение чисел согласно заданному алгоритму;
§ оценить погрешность вычисления после перевода результата в исходную систему счисления.
2. Алгоритм выполнения операции сложения.
3. Структурную схему вычислительного устройства, выполняющего сложение и умножение, содержащую узлы для действия над мантиссами и порядками, а также при этом необходимо определить время умножения с учетом временных задержек в комбинационных схемах.
4. Функциональные схемы основных узлов проектируемого сумматора-уножителя в заданном логическом базисе. Для этого следует провести:
§ логический синтез комбинационного одноразрядного четверичного сумматора (ОЧС) на основе составленной таблицы истинности для суммы слагаемых с учетом переноса из младшего разряда, используя при этом карты Карно-Вейча или алгоритм извлечения (Рота), оценив эффективность минимизации;
§ логический синтез одноразрядного комбинационного четверичного умножителя (ОЧУ) в случае разработки структурной схемы 1-го типа путем минимизации переключательных функций по каждому выходу схемы. Минимизация выполняется с применением алгоритма Рота или карт Карно-Вейча с последующей оценкой эффективности минимизации;
§ логический синтез одноразрядного комбинационного четверичного умножителя-сумматора (ОЧУС) в случае разработки структурной схемы 2-го типа путем минимизации переключательных функций по каждому выходу схемы. Минимизация выполняется с применением алгоритма Рота или карт Карно-Вейча с последующей оценкой эффективности минимизации;
§ логический синтез комбинационной схемы преобразователя множителя (ПМ);
§ построить функциональную схему ОЧС в заданном логическом базисе и на мультиплексорах;
§ построить функциональную схему ПМ и ОЧУ (ОЧУС) в заданном логическом базисе.
По результатам разработки определить время умножения на один разряд и на n разрядов множителя.
Исходные данные к расчетной работе
Исходные данные для выполнения расчетной работы (приведены в прил.):
1. Исходные операнды - десятичные числа с целой и дробной частью, над которыми производится операция умножения (заданы в строке 1 табл. П.1);
2. Алгоритм выполнения операции умножения: А, Б, В, Г (определяется строкой 2 табл. П.1):
А – умножение начинается с младших разрядов множителя со сдвигом частичных сумм вправо,
Б – умножение начинается с младших разрядов множителя со сдвигом частичных произведений (множимого) влево,
В – умножение начинается со старших разрядов множителя со сдвигом частичных сумм влево,
Г – умножение начинается со старших разрядов множителя со сдвигом частичных произведений вправо.
3. Метод ускоренного умножения, на базе которого строится умножитель:
§ для алгоритмов А и Б: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах;
§ для алгоритмов В и Г: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в дополнительных кодах.
4. Двоичные коды четверичных цифр множимого для работы в двоично-четверичной системе счисления (вариант кодирования учитывается при выполнении арифметических операций и задается строкой 3 табл.П.1). Множитель представляется обычным весомозначным кодом: 04 ─ 00, 14 ─ 01, 24 ─ 10, 34 ─ 11.
5. Тип синтезируемого устройства умножения, определяемый основными структурными узлами, на базе которых строится умножитель:
§ умножитель 1-го типа строится на базе ОЧУ, ОЧС и регистра-аккумулятора;
§ умножитель 2-го типа строится на базе ОЧУС, ОЧС и регистра результата (см. строку 6 табл. П.1 ).
6. Способ минимизации и логический базис для аппаратной реализации ОЧУ, ОЧУС и ОЧС (определяется строками 4, 5, 6 табл. П.1), при этом ОЧС реализуется в заданном логическом базисе и на мультиплексорах.
Пример синтеза сумматора-умножителя (разработка алгоритма умножения и структурной схемы сумматора-умножителя)
Исходные данные:
исходные сомножители: Мн = 15,55; Мт = - 45,35;
алгоритм умножения: А;
метод умножения: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах;
коды четверичных цифр множимого для перехода к двоично-четверичной системе кодирования:04 ® 00, 14 ® 11, 24 ® 10, 34 ® 01;
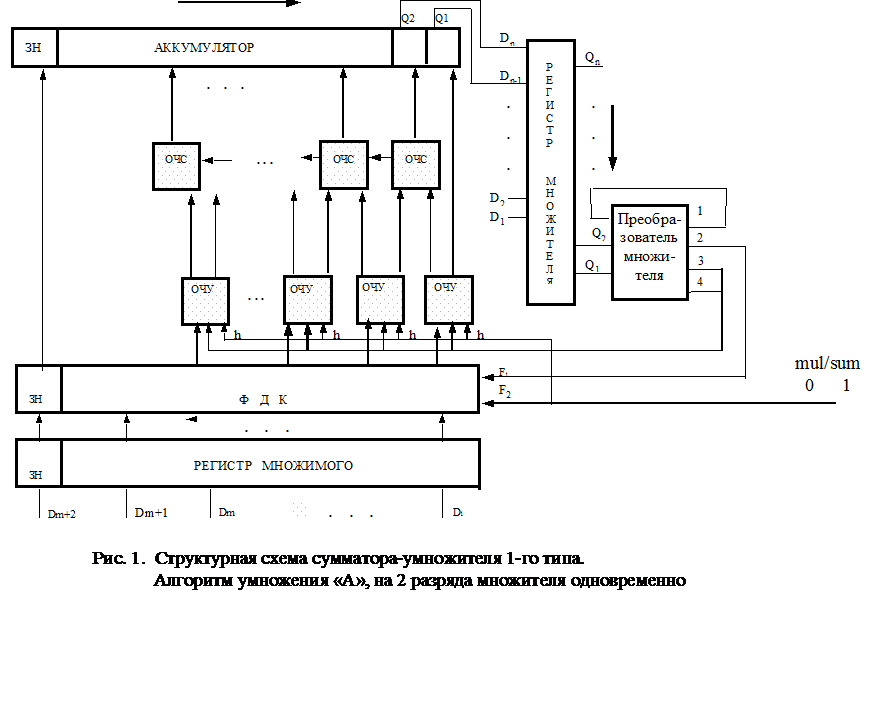
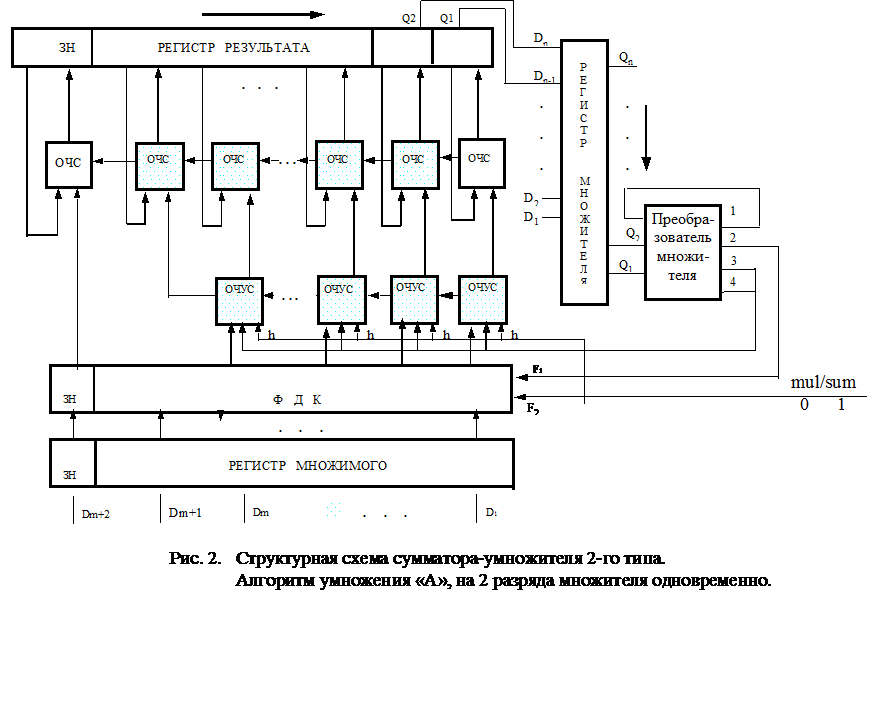
тип синтезируемого умножителя: структурные схемы приведены для обоих типов умножителей - на рис.1 приведена структура 1-го типа (ОЧУ, ОЧС, аккумулятор), на рис.2 приведена структура 2-го типа (ОЧУС, ОЧС, регистр результата).
Арифметические операции сложения двоично-четверичных чисел с разными знаками в дополнительных кодах и умножения на 2 разряда множителя в прямых кодах должны выполняться одним цифровым устройством, именуемым сумматор-умножитель. Учитывая то, что суммирующие узлы обязательно входят в состав умножителя, начнем синтез с разработки алгоритма умножения.
Множимое
15 | 4 0,55 Мн4 =33,2030
12 3 4 в соответствии с заданной кодировкой
3 2,20 множимого
4 Мн2/4 = 0101,10000100
0,80
4
3,20
4
0,80
Множитель
45| 4 0,35 Мт4 = -231,112
44 11 | 44
1 8 2 1,40 Мт2/4 = -101101,010110
3 4 множитель представляется обычным
1,60 весомозначным кодом: 04 - 00, 14 - 01,
4 24 - 10, 34 - 11
2,40 для всех вариантов
4
1,60
2. Запишем сомножитель в форме с плавающей запятой в прямом коде:
Мн = 0,010110000100 РМн = 0.0010 +0210 - закодировано по заданию,
Мт = 1,101101010110 РМт = 0.0011 +0310 - закодировано традиционно.
3. Умножение двух чисел с плавающей запятой на два разряда множителя одновременно в прямых кодах. Это сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму, и перемножению мантисс сомножителей.
Порядок произведения будет равен:
РМн = 0.0010 02
РМт = 0.001103
РМн·Мт = 0.1111 11.
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак произведения определяется суммой по модулю ”два” знаков сомножителей, т.е.
зн Мн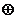 
зн Мт = 0 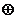1 = 1.
Для умножения мантисс необходимо предварительно преобразовать множитель. При умножении чисел в прямых кодах диада 11(34) заменяется на триаду 1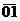 
. Преобразованный множитель имеет вид: Мтп4 = 1 
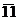1112 или Мтп2= 01 01010110. Перемножение мантисс по алгоритму “А” приведено в табл. 1.
4. После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение (Мн·Мт4 = -0,23000331002, РМн ·Мт = 5) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
Мн · Мт4 = -23000,331002 РМн ·Мт = 0;
Мн · Мт10 = - 704,9884.
Перемножение мантисс. Таблица 1.
| Четверичная с/с | Двоично-четверичная с/с | Комментарии | |||||
| 0. | 0. | 00 00 00 00 00 00 00 | S0ч= 0 | ||||
| 0. | 1330120 | 0. | 11 01 01 00 11 10 00 | П1ч = Мн · 2 | |||
| 0. | 0. | 11 01 01 00 11 10 00 | S1ч | ||||
| 0. | 0. | 00 11 01 01 00 11 10 | S1ч · 4-1 | ||||
| 0. | 0332030 | 0. | 00 01 01 10 00 01 00 | П2ч = Мн · 1 | |||
| 0. | 0. | 11 11 01 11 11 00 10 | S2ч | ||||
| 0. | 0. | 00 11 11 01 11 11 00 | 10 00 | S2ч · 4-1 | |||
| 0. | 0332030 | 0. | 00 01 01 10 00 01 00 | П3ч = Мн · 1 | |||
| 0. | 0. | 11 11 11 11 10 00 00 | 10 00 | S3ч | |||
| 0. | 0. | 00 11 11 11 11 10 00 | 00 10 00 | S3ч · 4-1 | |||
| 0. | 0332030 | 0. | 00 01 01 10 00 01 00 | П4ч = Мн · 1 | |||
| 0. | 0. | 11 11 00 01 10 11 00 | 00 10 00 | S4ч | |||
| 0. | 0. | 00 11 11 00 01 10 11 | 00 00 10 00 | S4ч · 4-1 | |||
| 3. | 3001310 | 1. | 01 00 00 11 01 11 00 | П5ч = Мн · (-1) | |||
| 3. | 1. | 01 11 11 10 10 01 11 | 00 00 10 00 | S5ч | |||
| 3. | 1. | 01 01 11 11 10 10 01 | 11 00 00 10 00 | S5ч · 4-1 | |||
| 3. | 3001310 | 1. | 01 00 00 11 01 11 00 | П6ч = Мн · (-1) | |||
| 3. | 2313133 | 1. | 10 01 11 01 11 01 01 | 11 00 00 10 00 | S6ч | ||
| 3. | 1. | 01 10 01 11 01 11 01 | 01 11 00 00 10 00 | S6ч · 4-1 | |||
| 0. | 0332030 | 0. | 00 01 01 10 00 01 00 | П7ч = Мн · 1 | |||
| 0. | 0. | 00 10 01 00 00 00 01 | 01 11 00 00 10 00 | S7ч |
Результат прямого перемножения операндов дает следующее значение:
Мн10 · Мт10 = 15,55 · 45,35 = 705,1925.
Абсолютная погрешность:
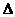= 705,1925 – 704,9884 = 0,2041.
Относительная погрешность:
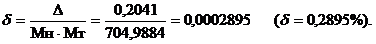
Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.
Литература
1. Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высшая школа, 1985.
2. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. Мн.: Вышейшая школа, 1980.
3. Лысиков Б.Г. Цифровая вычислительная техника. Мн.: , 2003 г.
4. Луцик Ю.А., Лукьянова И.В., Ожигина М.П. – Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ ,2001 г.
5. Луцик Ю.А., Лукьянова И.В.– Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ ,2004 г.
ПРИЛОЖЕНИЕ
Таблица П1. Исходные данные к расчетной работе
| №вар. | ||||||||||||||||||||||||
| Сомножители в десятичной системе счисления | ||||||||||||||||||||||||
| Мн | 43,34 | 81,92 | 65,91 | 15,44 | 36,39 | 48,51 | 68,39 | 28,69 | 73,48 | 49,27 | 72,34 | 67,83 | 56,59 | 29,63 | 52,26 | 48,27 | 84,19 | 16,35 | 31,50 | 72, 95 | 37, 32 | 28, 12 | 78, 11 | 42, 97 |
| Мт | 32,65 | 44,35 | 17,39 | 47,31 | 53,25 | 69,11 | 16,71 | 21,59 | 49,13 | 38,70 | 35,44 | 25,37 | 18,27 | 63,29 | 83,31 | 72,23 | 55,13 | 67,21 | 45,17 | 67, 65 | 28, 15 | 69, 97 | 25, 17 | 55, 39 |
| Алгоритм выполнения операции умножения | ||||||||||||||||||||||||
| А | Б | В | Г | А | Б | В | Г | А | Б | В | Г | А | Б | В | Г | А | Б | В | Г | А | Б | В | Г | |
| Варианты кодирования четверичных цифр двоичными кодами | ||||||||||||||||||||||||
| “0” | ||||||||||||||||||||||||
| “1” | ||||||||||||||||||||||||
| “2” | ||||||||||||||||||||||||
| “3” | ||||||||||||||||||||||||
| Логический базис для реализации ОЧС (см. табл.2) и метод минимизации. | ||||||||||||||||||||||||
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А1 | А2 | А3 | |
| Карты Карно-Вейча | Алгоритм Рота | |||||||||||||||||||||||
| Логический базис для реализации ОЧУ(ОЧУС, см. табл.2) и метод минимизации. | ||||||||||||||||||||||||
| А4 | А5 | А6 | А7 | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А1 | А2 | А3 | А4 | А5 | А6 | |
| Алгоритм Рота | Карты Карно-Вейча | |||||||||||||||||||||||
| Тип реализуемой структурной схемы | ||||||||||||||||||||||||
Таблица П2 Логический базис для реализации схем
| Функционально полный Логический базис | Базовые логические Элементы | |||||||||
|  x х1х2 х1 + х2 |
| ||||||||
    A2 | х1х2 x1Åx2 |
| ||||||||
  A3 | х1+х2 x1Åx2 |
| ||||||||
    А4 | х1х2 _ Х |
| ||||||||
   А5 | х1+х2 _ Х |
| ||||||||
   А6 |  х1х2 |
| ||||||||
  А7 |  х1+х2 |
|
Содержание
Задание к расчетной работе. 3
Исходные данные к расчетной работе. 4
Пример синтеза сумматора-умножителя (разработка алгоритма умножения и структурной схемы сумматора-умножителя) 5
Разработка алгоритма умножения. 5
Разработка структурной схемы сумматора-умножителя. 1
Синтез структуры сумматора-умножителя 1-го типа. 2
Синтез структуры сумматора-умножителя 2-го типа. 2
Разработка функциональных схем основных узлов сумматора-умножителя. 4
Логический синтез одноразрядного четверичного умножителя. 4
Логический синтез одноразрядного четверичного сумматора. 6
Логический синтез одноразрядного четверичного умножителя-сумматора. 13
Синтез комбинационных схем устройств умножения на основе мультиплексоров 16
Литература. 21
ПРИЛОЖЕНИЕ. 23
Таблица П1. Исходные данные к расчетной работе. 23
Таблица П2 Логический базис для реализации схем. 25
Св. план , поз.
УЧЕБНОЕ ИЗДАНИЕ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
к расчетной работе
по курсу
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
для студентов специальности
”Вычислительные машины, системы и сети”
всех форм обучения
Составители: Лукъянова Ирина Викторовна
Луцик Юрий Александрович
Редактор
Корректор
Компьютерная верстка
Подписано в печать . . Формат 60х84 1/16. Бумага офсетная.
Гарнитура Times New Roman. Печать ризографическая. Усл. печ. л. .
Уч.- изд. л. . Тираж экз. Заказ .
Издатель и полиграфическое исполнение:
Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Лицензия ЛП № 156 от 05.02. 2001.
Лицензия ЛВ № 509 от 03.08. 2001.
220013, Минск, П.Бровки, 6.
АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
для студентов специальности
”Вычислительные машины, системы и сети”
всех форм обучения
Минск 2006
УДК 004.7 (075.8)
ББК 32.97 я 73
Л 84
Лукьянова И.В., Луцик Ю.А.
| Л 84 | Арифметические и логические основы вычислительной техники: Методические пособие к расчетной работе / Ю.А. Луцик, И.В. Лукъянова, − Мн.: БГУИР, 2006. − с.: ил. . ISBN 985-444-642-5 |
| В методическом пособии приведены исходные данные для выполнения расчетной работы и рассмотрен пример выполнения и оформления расчетной работы для одного из вариантов задания. Пособие может быть использовано студентами всех форм обучения, специальности 40 02 01 ”Вычислительные машины системы и сети”, магистрантами и аспирантами. |
УДК 004.7 (075.8)
ББК 32.97 я 73
© Лукьянова И.В., Луцик Ю.А., 2006
ISBN 985-444-642-5 © БГУИР, 2006
Задание к расчетной работе
Расчетная работа предполагает синтез цифровых схем арифметических устройств, выполняющих операции сложения и умножения над числами, представленными в форме с плавающей запятой в двоичной и двоично-четверичной системах счисления (с/с).
По исходным данным необходимо разработать:
1. Алгоритм выполнения операции умножения, для чего потребуется:
§ перевести заданные исходные числа в четверичную систему счисления;
§ представить числа в форме с плавающей запятой, при этом число четверичных разрядов для мантиссы равно шести, для порядка – два, плюс два разряда для знаков мантиссы и порядка;
§ произвести перемножение чисел согласно заданному алгоритму;
§ оценить погрешность вычисления после перевода результата в исходную систему счисления.
2. Алгоритм выполнения операции сложения.
3. Структурную схему вычислительного устройства, выполняющего сложение и умножение, содержащую узлы для действия над мантиссами и порядками, а также при этом необходимо определить время умножения с учетом временных задержек в комбинационных схемах.
4. Функциональные схемы основных узлов проектируемого сумматора-уножителя в заданном логическом базисе. Для этого следует провести:
§ логический синтез комбинационного одноразрядного четверичного сумматора (ОЧС) на основе составленной таблицы истинности для суммы слагаемых с учетом переноса из младшего разряда, используя при этом карты Карно-Вейча или алгоритм извлечения (Рота), оценив эффективность минимизации;
§ логический синтез одноразрядного комбинационного четверичного умножителя (ОЧУ) в случае разработки структурной схемы 1-го типа путем минимизации переключательных функций по каждому выходу схемы. Минимизация выполняется с применением алгоритма Рота или карт Карно-Вейча с последующей оценкой эффективности минимизации;
§ логический синтез одноразрядного комбинационного четверичного умножителя-сумматора (ОЧУС) в случае разработки структурной схемы 2-го типа путем минимизации переключательных функций по каждому выходу схемы. Минимизация выполняется с применением алгоритма Рота или карт Карно-Вейча с последующей оценкой эффективности минимизации;
§ логический синтез комбинационной схемы преобразователя множителя (ПМ);
§ построить функциональную схему ОЧС в заданном логическом базисе и на мультиплексорах;
§ построить функциональную схему ПМ и ОЧУ (ОЧУС) в заданном логическом базисе.
По результатам разработки определить время умножения на один разряд и на n разрядов множителя.
Исходные данные к расчетной работе
Исходные данные для выполнения расчетной работы (приведены в прил.):
1. Исходные операнды - десятичные числа с целой и дробной частью, над которыми производится операция умножения (заданы в строке 1 табл. П.1);
2. Алгоритм выполнения операции умножения: А, Б, В, Г (определяется строкой 2 табл. П.1):
А – умножение начинается с младших разрядов множителя со сдвигом частичных сумм вправо,
Б – умножение начинается с младших разрядов множителя со сдвигом частичных произведений (множимого) влево,
В – умножение начинается со старших разрядов множителя со сдвигом частичных сумм влево,
Г – умножение начинается со старших разрядов множителя со сдвигом частичных произведений вправо.
3. Метод ускоренного умножения, на базе которого строится умножитель:
§ для алгоритмов А и Б: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах;
§ для алгоритмов В и Г: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в дополнительных кодах.
4. Двоичные коды четверичных цифр множимого для работы в двоично-четверичной системе счисления (вариант кодирования учитывается при выполнении арифметических операций и задается строкой 3 табл.П.1). Множитель представляется обычным весомозначным кодом: 04 ─ 00, 14 ─ 01, 24 ─ 10, 34 ─ 11.
5. Тип синтезируемого устройства умножения, определяемый основными структурными узлами, на базе которых строится умножитель:
§ умножитель 1-го типа строится на базе ОЧУ, ОЧС и регистра-аккумулятора;
§ умножитель 2-го типа строится на базе ОЧУС, ОЧС и регистра результата (см. строку 6 табл. П.1 ).
6. Способ минимизации и логический базис для аппаратной реализации ОЧУ, ОЧУС и ОЧС (определяется строками 4, 5, 6 табл. П.1), при этом ОЧС реализуется в заданном логическом базисе и на мультиплексорах.
Пример синтеза сумматора-умножителя (разработка алгоритма умножения и структурной схемы сумматора-умножителя)
Исходные данные:
исходные сомножители: Мн = 15,55; Мт = - 45,35;
алгоритм умножения: А;
метод умножения: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах;
коды четверичных цифр множимого для перехода к двоично-четверичной системе кодирования:04 ® 00, 14 ® 11, 24 ® 10, 34 ® 01;
тип синтезируемого умножителя: структурные схемы приведены для обоих типов умножителей - на рис.1 приведена структура 1-го типа (ОЧУ, ОЧС, аккумулятор), на рис.2 приведена структура 2-го типа (ОЧУС, ОЧС, регистр результата).
Арифметические операции сложения двоично-четверичных чисел с разными знаками в дополнительных кодах и умножения на 2 разряда множителя в прямых кодах должны выполняться одним цифровым устройством, именуемым сумматор-умножитель. Учитывая то, что суммирующие узлы обязательно входят в состав умножителя, начнем синтез с разработки алгоритма умножения.