Формула Бернулли и ее следствия

Пусть проводится n последовательных независимых одинаковых испытаний (экспериментов), в каждом из которых событиеА может появиться с одной и той же вероятностью p и не появиться с вероятностью 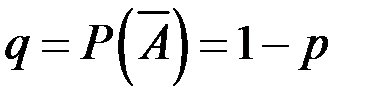. Вероятность появления события в каждом опыте не зависит от того, появилось или нет это событие в других экспериментах (т.к. испытания независимые).

Вероятность того, что в n независимых испытаниях событиеА появится ровно m раз 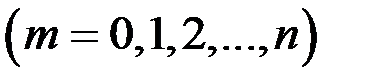, выражается формулой Бернулли

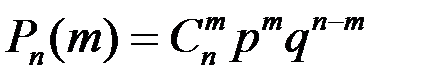, где .

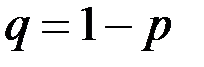Из формулы Бернулли вытекает ряд важных следствий, широко используемых на практике, в частности, при контроле качества изделий, в теории стрельбы, в теории связи и т.д.

Следствия формулы Бернулли

1. Вероятность того, что в серии из n опытов событиеА появится хотя бы один раз вычисляется по формуле: .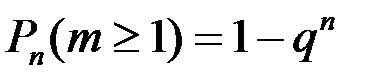

2. Вероятность того, что в серии из n опытов событиеА появится не менее k раз (k и больше) находится по формуле: .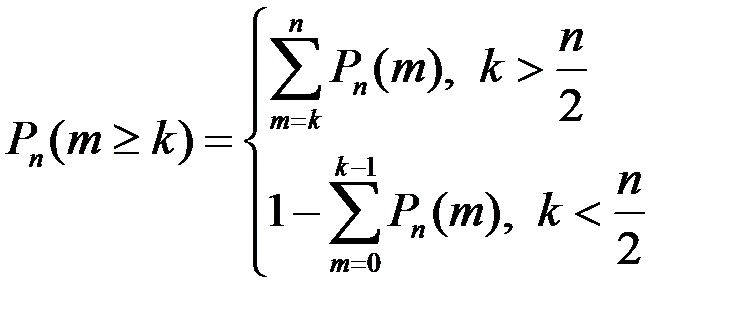

3. Вероятность того, что в серии из n опытов событиеАпоявится не более k раз (k и меньше) находится по формуле: .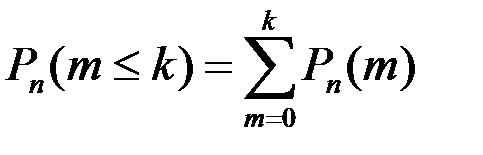

4. Число опытов необходимых для того, чтобы событие А появилось хотя бы один раз с вероятностью не менее заданной Р находится по формуле: 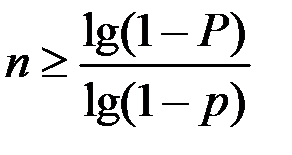, где Р – заданная вероятность, р – вероятность появления событияА в каждом опыте.

5. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число 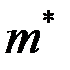наступлений событияА в nиспытаниях заключено между числами np-q и np+p .

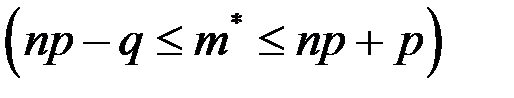Пример 1

Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.

Решение

Поскольку 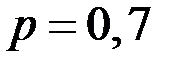, то 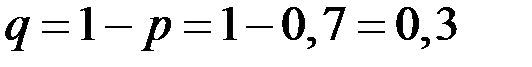. По условию 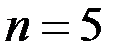, , 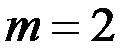по формуле Бернулли получим

.

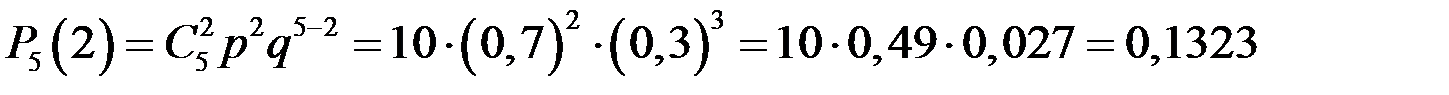Пример 2

Для нормальной работы автобазы на линии должно быть не менее восьми машин, а имеется их десять. Вероятность невыхода каждой машины на линию равна 0,1. Найти вероятность нормальной работы автобазы на ближайший день.

Решение

Автобаза будет работать нормально (событие D), если на линию выйдет или восемь (событие А), или девять (событие В), или все десять (событие С) автомашин.

По теореме сложения вероятностей

.

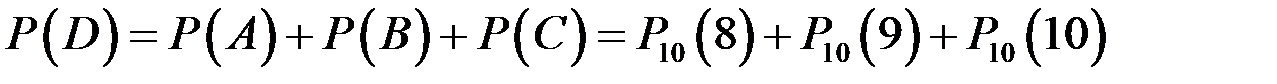Каждое слагаемое найдем по формуле Бернулли. Поскольку вероятность невыхода каждой автомашины на линию равна 0,1, то вероятность выхода автомашины на линию будет равна 0,9, т.е. 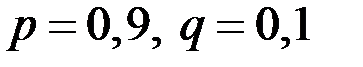. Из условия следует, что 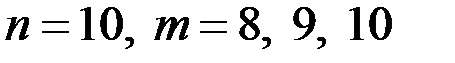. Следовательно,

.

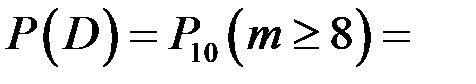
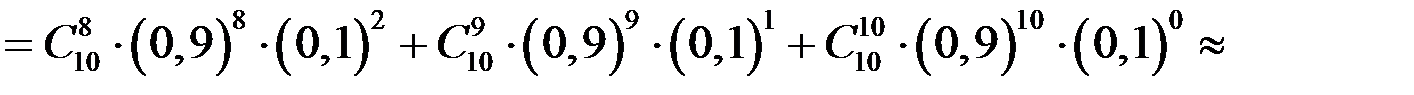
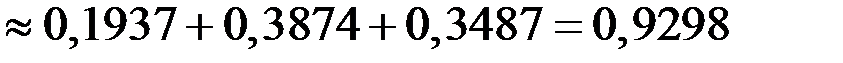Пример 3

Вероятность попадания в мишень при одном выстреле равна 0,8. Найти наиболее вероятное число попаданий в мишень при 5 выстрелах и соответствующую этому числу вероятность.

Решение

Воспользуемся неравенством

.

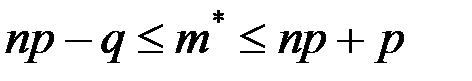Поскольку 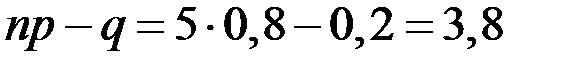, , 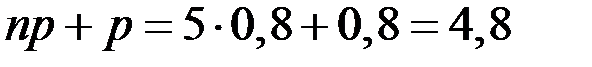то 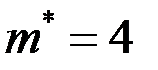. Вероятность 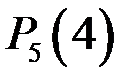находим по формуле Бернулли:

.

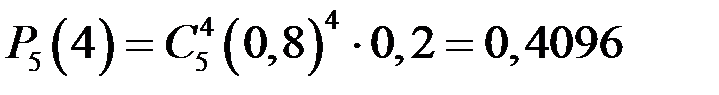Пример 4

Вероятность того, что наудачу взятая деталь нестандартная 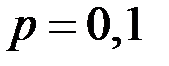. Найти вероятность того, что среди 5 деталей будет не более двух нестандартных (событие А).

Решение

Искомую вероятность находим, используя следствие из формулы Бернулли:

.
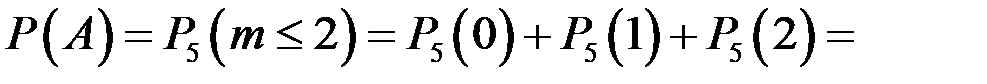
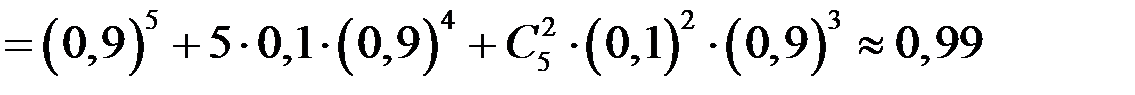