Решение многошаговых задач оптимизации методом динамического программирования

Во многих динамических задачах время рассматривается непрерывно, или как дискретная величина. Задачи такого типа называются многошаговыми (многоэтапными) задачами оптимизации. Их можно решать методом динамического программирования.

В многошаговых задачах оптимизации время принимает дискретные значения: .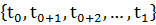

Состояние системы в момент времени 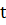задается вектором: 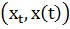, где , .

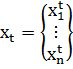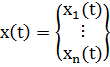В уравнении в момент времени 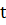задается 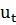дискретными значениями.

Рассмотрим простейшую многошаговую систему - одношаговую систему. Начальное состояние системы записывается известным вектором состояния 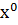. Выбор некоторого управления 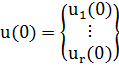определяет переход системы из 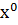в состояние 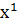. Этот переход описывается соотношениями: .

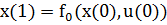Для многошаговых систем будем иметь

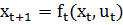, где 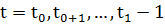; (11)

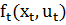– вектор, составленный из непрерывно дифференцируемых функций текущего состояния 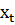и текущих значений управления .

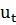Блок-схема многошагового процесса имеет вид (Рис.2):

X(1)

X( -1)

X( )

X(2)

X(0)

…

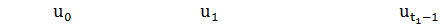
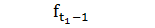
Рис.2

Здесь 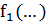вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управляющих параметров.

Предполагаем, что заданное начальное состояние 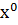- фиксированное. Требуется найти такую последовательность векторов 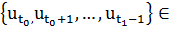фиксированной области управления 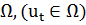, где 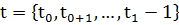, которая максимизирует целевую функцию

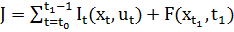
Таким образом, данная задача аналогична задачи оптимального управления с непрерывным временем – дискретная задача – многошаговая задача оптимального управления.

Подход динамического программирования в данном случае состоит в том, что решаемая задача “погружается ” в более широкий класс задач, описываемых рядом параметров, и вслед за этим, используя принцип оптимальности Беллмана, определяется основное рекуррентное соотношение.

Первый подход.

Возьмем в качестве параметров многошаговой задачи оптимизации начальный момент времени 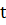и начальное состояние 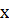. Тогда функция оптимального поведения равна оптимальному значению целевой функции J задачи с начальным состоянием 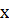и начальным моментом времени 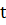. Тогда оптимальное значение целевой функции исходной задачи равно: 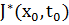. Согласно принципу оптимальности Беллмана:

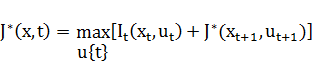, где , .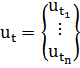

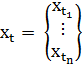Это означает, что оптимальное значение целевой функции с наименьшим состоянием 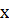и наименьшим моментом времени 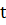равно оптимальному значению функции 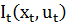в момент времени 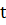и оптимальному значению функции оптимального поведения 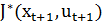в момент времени 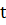. Можно представить все рекуррентные соотношения в виде:

.

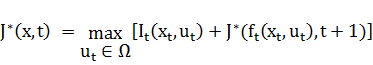Для этого соотношения граничное условие будет: 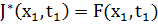- – показывает, что оптимальное значение целевой функции с начальным состоянием 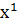в момент времени 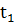равно (совпадает) со значением функции конечных параметров, рассчитанных при 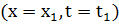. Данная задача аналогична задачи оптимального управления с непрерывным временем.

Второй подход.

Другой подход при решении многошаговых задач оптимизации состоит в том, что в качестве характеристических параметров выбираются не начальные состояния и не начальный момент времени, а начальное состояние и промежуток времени, остающийся до конечного момент времени.

Тогда ФОП 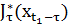– которая представляет собой оптимальное значение целевой функции с начальным состоянием 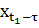, разворачивающаяся в промежутке протяженностью 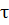. Оптимальное значение целевой функции исходной задачи соответственно равно: 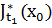– когда 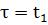. В этом случае последовательность решений определяется методом динамического программирования в порядке, обратном тому, который рассматривается до сих пор.

Первым членом этой последовательности является: 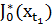, то есть оптимальное значение целевой функции с временным промежутком нулевой протяженности, начинающейся (и заканчивающейся) в 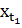. Оптимальное значение целевой функции этой задачи равно функции конечных параметров: .

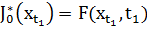Рассмотрим 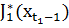– оптимальное значении целевой функции, задачи с промежутком равным одной единице времени 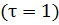, начинающегося в 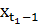. Эта задача называется первым шагом.

Оптимальное значение в этой задачи определяется как максимум значения суммы той части целевой функции, которая соответствует указанному времени, и оптимальное значение задачи с моментом времени 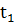с управляющим вектором :

.

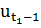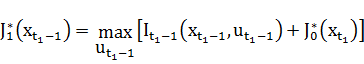Используя уравнение перехода: 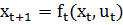, получаем

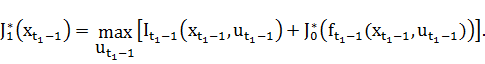
Данный выбор управления на первом шаге согласуется с принципом оптимальности Беллмана, поскольку управление 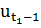- оптимально, то по отношению к состоянию 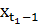, которое достигается в результате 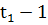предыдущих выборов управляющих векторов.

Аналогично этому, на втором шаге (в задаче с промежутком равным двум промежуткам времени) получим

.

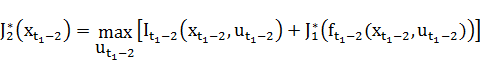Общее рекуррентное соотношение на шаге с номером 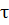выглядит следующим образом

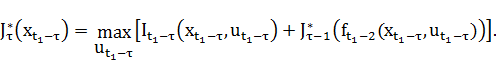
В рассмотренной задаче, оптимальное значение равно: 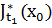– является оптимальным значением последней задачи в последовательности одношаговых задач оптимизации, описываемых функциональным уравнением, при 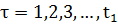, с граничным условием: 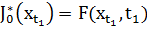. Вместо того, что бы решать эту задачу методом НЛП (выбирать сразу 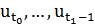), то здесь мы решаем последовательность одношаговых задач оптимизации.

Пример решения задачи оптимизации методом динамического программирования

В качестве примера применения подхода динамического программирования к многошаговым задачам оптимизации, в которых требуется найти набор из неотрицательных чисел 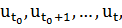максимизируем сепарабельную функцию (функция называется сепарабельной, если она представляет собой сумму функций, каждая из которых зависит только от одной переменной), при условии, что сумма этих чисел равна фиксированном числу .

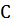Постановка задачи.

Найти ,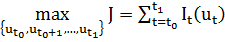

при ограничениях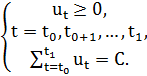

Решение:

Будем решать данную задачу методом динамического программирования. В данной задаче можно интерпретировать постоянную 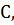как общий уровень имеющихся ресурсов и рассматривать ее в качестве параметра задачи. Обозначим через 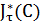– функцию оптимального поведения для процесса развертывания в момент времени 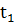с общим запасам ресурсов .

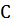Для процесса на временном промежутке протяженностью равной нулю и заканчивающегося для 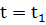будет

.

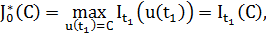
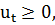
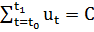Для одношагового процесса заканчивающегося в 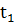, при этом надо распределять ресурсы между 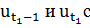огласно принципу оптимальности

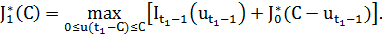
Общее рекуррентное соотношение имеет вид

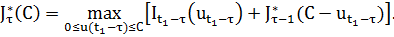
Решение задачи отыскивается с помощью общего рекуррентного соотношения, последовательно начиная с граничного условия 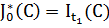, вплоть до шага (длина шага 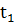) 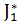(C).