Тема 2 Поле комплексных чисел

Определение. Полем комплексных чисел называется множество C, обладающее следующими свойствами:

1) С – поле,

2) R 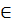C, R C.

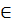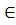3) i C, ,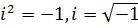

4) С с условиями 1,2,3 минимальное.

Алгебраическая форма комплексного числа

Определение. Пусть x и y – действительные числа. Число вида z = x + iy называется комплексным числом в алгебраической форме. x называют вещественной или действительной частью числа z и обозначают x = Re(z); y называют мнимой частью числа z и обозначают y = Im(z). Число i называют мнимой единицей, .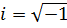

Пример z = 2 – 3i. Re(z) = 2, Im(z) = -3.

Определение. Два комплексных числа 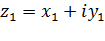, 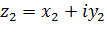называются равными, если, , .

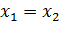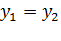Определение. Комплексное число z = x + iy равно 0, если x = 0 и y = 0.

Определение. Число 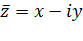называется сопряженным комплексному числу z = x + iy.

Действия над комплексными числами

1) – (a + bi) = – a – bi;

2) (a + bi) + (c + di) = (a + c) + (b + d) i;

3) (a + bi) - (c + di) = (a - c) + (b - d) i;

4) (a + bi) ∙ (c + di) = (ac - bd) + (bc + ad) i;

5) (a + bi)(a – bi) = ;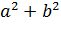

6) ;

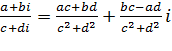7) Извлекать из комплексных чисел в алгебраической форме можно только корень второй степени.

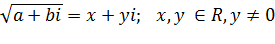
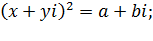
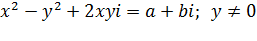
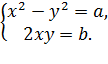
Решая систему находим х и у.

8) cтепени мнимой единицы.

Первой степенью числа i является само это число, тогда:

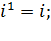
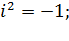
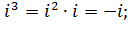
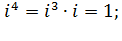
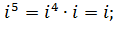
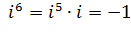
и так далее.

При любом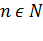

.

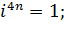
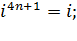
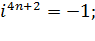
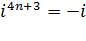Пример 1 Найти сумму (разность) комплексных чисел:

а) (2 + i)+ (5 + 6i) = (2 + 5) + (1 + 6)i = 7 + 7i,

б) (5 + 7i) + (2 - 6i) = (5 + 2) + (7 - 6)i = 7 + i,

в) (6 - 4i) + (- 15 - 2i) = (6 - 15) + (- 4 - 2)i = -9 - 6i,

г) (5 + 6i) - (3 + 7i) = (5 - 3) + (6 - 7)i = 2 - i.

Пример 2 Решить уравнение (5x + 3yi) + (2y - xi) = 9 + 5i.

Сложив комплексные числа в левой части уравнения получим

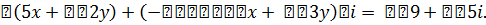
Два комплексных числа равны, если равны их действительные части и равны мнимые части, т.е.

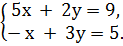
Решением данной системы уравнений будет x =1 и y = 2.

Пример 3 Найти произведение комплексных чисел:

1) (2 + 3i) ∙ (6 - 5i) = (2 ∙ 6 - 3 ∙ (- 5)) + (2 ∙ (- 5i) + 3i ∙ 6) = 27 + 8i,

2) (1 + i) ∙ (1 + i) = 1+ i + i + i² = 1 + 2i -1 = 2i,

3) (2 + 3i) ∙ (2 - 3i) = 4 - 6i + 6i - 9i² = 4 + 9 = 13.

Пример 4 Найти z если (2 - 3i) ∙ z = -1 - 5i.

Пусть z = a + bi, тогда

(2 - 3i) ∙ (a + bi) = (2a + 3b) + (- 3a + 2b)i = -1- 5i,

что равносильно системе уравнений

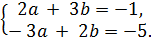
Решением данной системы уравнений будет a =1, b = -1, т.е. z = 1- i.

Проверим полученное решение

(2 - 3i) ∙ z = (2 - 3i) ∙ (1- i) = 2 - 2i - 3i + 3i 2 = -1- 5i.

Пример 5 Найти частное 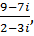2 - 3i ≠ 0 + 0i.

.

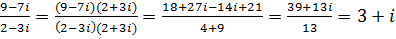Пример 6 Вычислить:

,

.

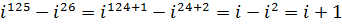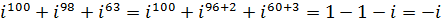Задачи для решения

1 Вычислить в алгебраической форме:

а) (3 + 6i) + (- 3 - 5i),

б) (- 9 - 4i) + (- 2 - 3i),

в) (- 3-i)³,

г) (1 + 6i) + (1 - 6i)² - (4 + i)³ + (- 4 + i),

д) (7 + 4i)² + 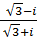+ (5 + i) ∙ (5 - i),

е) (1+ i)³ + 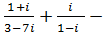(6 + 4i) ∙ (- 6 + 4i),

ж) 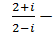(2 + 3i) + (5 - 3i),

з) ,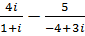

и) ,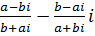

к) ,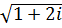

л) 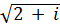- (9 - i) ∙ (7 + 2i) ∙ (7 + 3i) - .

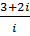2 Решить уравнение в действительных числах:

а) (2x - 5yi) + (3y + 2xi) = 13 - i,

б) 7 (3x + 2yi) + (2y - i) = 19 + 3.

3 Найти z, если:

а) z ∙ (2 + i)=15, б) (2 + 2i) ∙ z = 8i.

4 Доказать равенство:

.

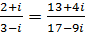5 Вычислить:

а) ;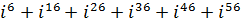

б) .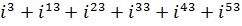

Геометрическая форма комплексного числа

Комплексное число z = х + уi можно охарактеризовать упорядоченной парой вещественных чисел (х, у), где х – действительная часть, у – мнимая часть числа z.

Такую пару чисел можно отождествить с точкой на плоскости, если на ней задана система координат (рисунок 1).

Множество всех комплексных чисел находится во взаимно однозначном соответствии с множеством всех точек плоскости.

Рисунок 1 – Геометрическая форма комплексного числа

Пример Комплексное число z = 3+ 2i можно отождествить с точкой A (3, 2), которую можно изобразить на плоскости XOY (рисунок 2). Комплексно-сопряженное число 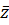= 3 - 2i изобразится точкой A (3, -2), симметричной точке A (3, 2) относительно действительной оси. Точки B (0, 1) и C (- 2, 0) соответствуют комплексным числам z = 0 + i и z = -2 + 0i (рисунок 2).

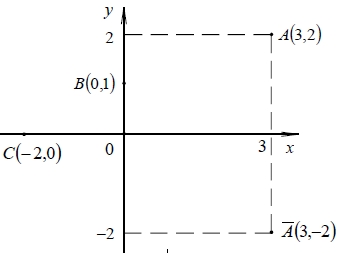
Рисунок 2 – Пример построения геометрической формы

Задачи для решения

1 Записать комплексные числа, сопряженные данным. Изобразить данные и сопряженные к ним комплексные числа точками на плоскости:

а) 1+ i; б) 4 - 7i; в) 3;

г) 3i; д) -1- 3i; е) 3 + 6i;

ж) - 3 - 5i; з) 2 + 3i; и) - 9 - 4i; к) 15- i.