Общая постановка динамической задачи разработки управленческого решения

Задача разработки управленческого решения переходит в категорию динамических в том случае, когда входящие в ее состав параметры оказываются функциями времени. Следует отметить, что в некоторых задачах время может рассматриваться как ресурс. Его специфической особенностью является то обстоятельство, что расходом времени невозможно управлять. Вместе с тем учет времени как ресурса оказывается принципиальным для целого класса задач, в основе которых лежит, например, требование минимизации времени, затрачиваемого на выполнение работы.

В других задачах время может выступать в качестве дополнительного параметра, значение которого изменяется самопроизвольно по известному закону. Динамические задачи разработки управленческого решения могут рассматриваться как в предположении непрерывности времени как аргумента, так и в предположении, что значимые параметры задачи определяются только в некоторые фиксированные моменты времени. В первом случае говорят о непрерывных динамических задачах, а во втором о дискретных. Математически при переходе от непрерывной задачи к дискретной непрерывное время заменяется неким набором дискретных отсчетов , где 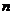- номер отсчета, а - шаг дискретизации, - номер отсчета. Обычно рассматривают эквидистантные задачи, для которых . Наконец, в некоторых случаях число рассматриваемых моментов времени может быть конечным.

Формально динамическая задача разработки управленческого решения может быть описана следующим выражением:

Дискретное представление исходных параметров заставляет вводить в рассмотрение не интегральные зависимости, а суммы. Формально такая замена проводится достаточно легко, однако в этой операции имеется ряд тонких моментов, которые необходимо принимать во внимание. К их числу следует в первую очередь отнести размер выборки . Если число сравнительно велико, а шаг дискретизации оказывается относительно небольшим, процедура дискретизациипараметра не оказывает существенного влияния на результат решения (рис. 21 a).

Рис. 21 Дискретизация непрерывного процесса с маленьким а) и большим б) шагами

Ситуация существенно меняется в том случае, когда за время интервала дискретизации параметр успевает существенно измениться, а само число его отсчетов невелико (рис. 21 б). Если в первом случае можно говорить о приближенном дискретном представлении непрерывного параметра, то во втором речь идет о существенном искажении вида параметра, что приводит к серьезным изменениям в структуре решения и может дать существенно отличные результаты.

На настоящий момент отсутствует исчерпывающая классификация динамических задач разработки управленческого решения, поэтому далее представлена коллекция различных вариантов их постановки и методов решения.

Метод сетевого планирования

В основе методов сетевого планирования лежит так называемый сетевой граф, пример которого показан на рис. 22. В кружках графа обычно отмечают различные события, например «Завершены монтажные работы». Стрелки графа означают собственно работу, которая может потребовать определенных ресурсов, в том числе и времени. Важной особенностью сетевого графа является возможность определения полного времени, которое требуется на выполнение работы. Оно определяется так называемым критическим путем, который представляет собой последовательность событий, достижение которых требует максимально большого времени. Очевидно, что если бы граф не имел разветвлений, то полное время выполнения работ совпадало бы с суммой времен, затраченных на каждую работу. Однако, в случае ветвлений, некоторые из работ параллельных ветвей могут быть завершены раньше. Тогда полное время выполнения параллельных работ определяется временем выполнения самой длинной работы. Она и оказывается на критическом пути.

Применительно к сетевому графику может быть поставлена задача оптимизации использования материальных, трудовых и финансовых ресурсов. Например, если имеется несколько параллельных ветвей графа, то работа, лежащая на критическом пути, обязательно должна быть обеспечена всеми необходимыми ресурсами. В то же время остальные работы могут, при необходимости, начаты с некоторой задержкой. Эта задержка может быть запланирована и использована для того, чтобы один и тот же ресурс первоначально использовался для выполнения одной работы, а потом другой. Время окончания любой работы должно быть согласовано с временем окончания работы, лежащей на критическом пути, поскольку иначе задержанная с началом работа сама окажется на критическом пути.

Рис. 22. Пример сетевого графа выполнения строительных работ

Сетевой график может рассматриваться как в условиях определенности, так и в условиях риска и неопределенности. В случае риска можно говорить и среднем времени выполнения работы и рассчитывать его теми же методами, которые использовались при решении статических задач. Аналогично в случае неопределенности можно рассматривать оптимальные стратегии.

Сетевые графики широко используются в современной методологии управления различными видами деятельности, имеющими четко обозначенное начало и конец, и получившими название «Управление проектами». Проект – комплекс взаимосвязанных мероприятий, предназначенных для достижения в течение заданного времени и при установленном бюджете поставленных задач с четко определенными целями.

Для поддержки проекта существуют специальные программные средства, позволяющие автоматизировать многие операции, связанные с разработкой, оптимизацией и реализацией проекта. На рис. 23 показан пример выдачи программой пакета Microsoft Project последовательности работ проекта в виде так называемой диаграммы Ганта. Удобство такой диаграммы заключается в том, что система сразу выделяет цветом работы, находящиеся на критическом пути, а также дополнительно выдает информацию о сроках (датах) каждой работы. Кроме этого, система может строить и обычный сетевой график (рис. 24), отображать загрузку и расход ресурсов, контролировать ход выполнения проекта, в том числе и расход его сметы и многое другое.

Рис. 23. Диаграмма Ганта.