Метод Монте-Карло при решении задачи в условиях риска

Метод предусматривает существование алгоритмической и программной модели решения задачи и замену реального случайного процесса его имитацией от датчика случайных чисел. Свое название метод Монте-Карлополучил по имени казино, находящегося в княжестве Монако в одноименном городе, в котором исторически было сосредоточено большое число игровых заведений. Вероятно первые разработчики этого метода на основе анализа последовательностей случайных чисел, генерируемых колесом рулетки, пытались создать методику выбора очередного числа, на которое и должна была бы быть сделана ставка. Поскольку возможностей для непосредственных экспериментов в здании казино нет, было предложено определить закон распределения чисел для конкретного стола, а далее имитировать эту последовательность в лабораторных условиях с целью отыскания необходимого алгоритма. Заметим, что поскольку казино в Монако существуют до сих пор, этот эксперимент закончился неудачей.

В соответствии с методом Монте-Карло на основании известной функции распределения случайного процесса генерируется выборка значений от датчика случайных чисел. В современной практике используется программная генерация таких чисел на основе стандартных и относительно несложных алгоритмов. Подобный подход позволяет, при необходимости, повторить генерацию выборки с заданным законом распределения или создать новую с тем же законом. Одним из недостатков программного метода является возникающая в некоторых случаях периодичность значений, борьба с которой ведется за счет настройки датчика. Тем не менее, говорить о том, что программным методом генерируется последовательность полностью случайных чисел, не приходится. Поэтому в литературе программные датчики называют обычно датчиками псевдослучайных чисел.

Для решения задачи разработки управленческого решения методом Монте-Карло также необходимо знать функцию распределения случайного параметра. Если она известна, то исследователь может отказаться от реальных данных, получение которых сопряжено с известными трудностями, и заменить их выборками значений от программного датчика. Количество таких значений может существенно превышать объемы реальных выборок, но, в случае совпадения законов распределения реальных и сгенерированных данных, точность получаемых результатов существенно возрастает. При решении задачи в Excel для вызова датчика случайных чисел необходимо включить надстройку Анализ данных, в пункте Сервис главного меню выбрать пункт Анализ данных, а в открывшемся меню Инструменты анализа пункт Генерация случайных чисел.

Основной задачей использования метода является построение функции распределения целевой функции с сохранением полученных для каждого значения решений. Далее на ее основе выбирается оптимальное решение, соответствующее вероятности (при симметричной функции распределения) при М-постановке или с заданным значением вероятности при Р-постановке, как это делалось при реализации алгоритмического метода.

Для каждого значения сгенерированного датчиком случайных чисел параметра решается оптимизационная задача и определяется значение критериальной функции и соответствующее ей решение. Далее строится гистограммараспределения критериальной функции, на основе которой принимается решение.

Примечание. Гистограмма (эмпирическая плотность распределения) строится следующим способом. Проводится разбиение оси аргументов на конечное число граничащих друг с другом промежутков . Затем подсчитывают число значений, полученных в нашем случае от датчика случайных чисел, лежащих в диапазоне . Эти числа называются групповыми частотами. Над рисуют прямоугольник высоты , где ‑ общее количество в нашем случае сгенерированных датчиком чисел. Возникающий ступенчатый график и есть гистограмма. Для получения эмпирической функции распределения (интегральная гистограмма распределения) строят ступенчатый график, у которого высота прямоугольника при есть сумма значений . Очевидно, что при правильной работе датчика случайных чисел при уменьшении и соответствующем увеличении 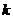эмпирическая функция распределения будет стремиться к заданной функции распределения случайного процесса [1].

Подобный способ удобен при наличии программной реализации задачи математического программирования в виде, например, самостоятельной функции. При использовании для расчетов Excel для построения гистограммы достаточно в пункте Сервис главного меню выбрать пункт Анализ данных, а в открывшемся меню Инструменты анализа пункт Гистограмма. В открывшемся меню необходимо указать диапазон значений случайных чисел, сгенерированных от датчика, и в качестве параметров вывода Интегральный процент.

При использовании надстройки Поиск решения каждый расчет требует некоторого количества ручных операций. Для уменьшения трудоемкости вычислений гистограмма распределения случайного параметра может быть построена до решения задачи оптимизации. В этом случае для расчета значений критериальной функции могут быть использованы средние значения карманов гистограммы, а соответствующие им значения критериальной функции встретятся в итоговом распределении столько раз, сколько они были в исходной гистограмме. Фактически задача в этом случае сводится к замене оцифровки оси абсцисс гистограммы распределения значениями критериальной функции при сохранении значений ординат.