Однокритериальная статическая задача разработки управленческого решения в условиях определенности

Альтернативы в задачах экономики и менеджмента сводится к различным вариантам использования ресурсов. К числу таких ресурсов можно отнести материальные, финансовые, людские и время. Время относится к особой категории ресурсов, расходом которых управлять невозможно. 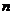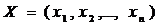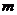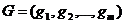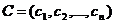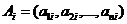Однокритериальная статическая задача управленческого решения в условиях определенности – это задача с набором из независящих от времени контролируемых параметров (параметров, которыми можно управлять в интересах решающего задачу) ; набором из не зависящих от времени ограничений ; набором не зависящих от времени неконтролируемых параметров, которые определяются условием задачи , , 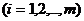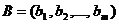; с одним не зависящим от времени критерием 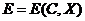. Формальная математическая запись однокритериальной статической задачи в условиях определенности имеет вид:

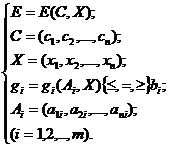
Решение такой задачи – это одна из альтернатив 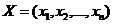. Она может быть выбрана случайно (случайное решение). Если набор таких альтернатив был заранее разработан, то, выбирая наилучшую из них по значению критериальной функции, мы имеем рациональное решение. Наконец, если мы можем воспользоваться оптимальным методом, то метод и должен автоматически определить наилучшую альтернативу 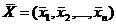из числа возможных. В этом случае будет обеспечено оптимальное (максимальное или минимальное) значение критерия 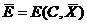при заданных значениях неконтролируемых параметров.

Очевидно, что случайные решения мало кого устраивают. При разработке рациональных решений перед принятием решения (выбором альтернативы) нам необходимо провести работу по разработке набора альтернатив, удовлетворяющих ограничениям задачи. В зависимости от конкретной задачи для выполнения такой работы нам может потребоваться достаточно много усилий, например, разработать несколько альтернативных проектов. Очень часто так и приходится поступать. В то же время, в нашем случае основной интерес представляет процесс выбора, а не разработки альтернативы. Поэтому для лучшего понимания метода нам было бы удобно генерировать альтернативы автоматически, что позволяют оптимальные методы. В принципе, мы можем воспользоваться любым известным нам оптимальным методом поиска экстремума функции. Поэтому для определенности для изучения способов решения однокритериальной статической задачи управленческого решения воспользуемся методами математического программирования.

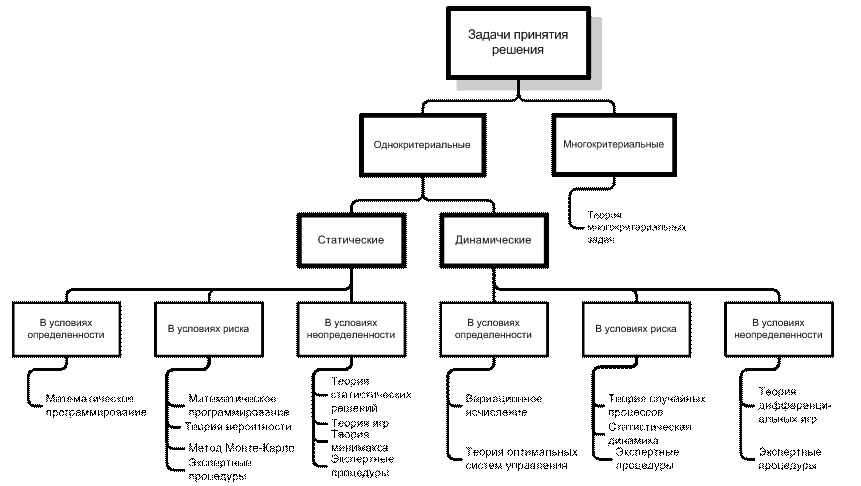
Рис. 16. Математическая классификация задач принятия решения

Задача Л.В. Канторовича (1, 2), рассматриваемая применительно к экономике и менеджменту, получила название производственной задачи или задачи распределения ресурсов. Действительно, если уравнение (1) описывает доход или прибыль от производственной деятельности, а выражения (2) описывают расход имеющихся принятых во внимание ресурсов, которые необходимы для осуществления производственной деятельности, то решение этой задачи позволяет получить оптимальную по критерию дохода или прибыли программу выпуска продукции 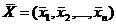. Полученное в этом случае максимальное значение целевой функции 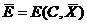есть ни что иное, как максимально возможный доход или прибыль, которые можно получить в конкретной ситуации. Таким образом, для постановки этой задачи необходимо придать конкретный смысл неконтролируемым параметрам 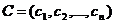, 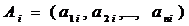и . 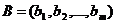Например, значения 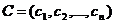могут быть отпускными ценами соответствующих наименований продукции, значения 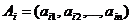- это коэффициенты расхода ресурса 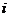на выпуск единицы продукции соответствующего вида, а 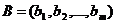‑ это наличие соответствующего ресурса.

Примечание. В задаче, решенной в процессе выполнения лабораторной работы номер 1, исходные данные были сформированы от датчика случайных чисел. Полученное решение математически является оптимальным, но оно никак не может быть интерпретировано по отношению к какой либо практической задаче. Если выбрать практическую задачу, решаемую методом линейного или математического программирования, и задать значения неконтролируемых параметров на основе реальных данных, то полученное решение имеет практический смысл.

Существует еще несколько вариантов постановки задачи, решаемой методами математического программирования. Задача о назначенияхимеет следующий смысл. Пусть имеется 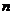кандидатов на 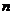должностей. Эффект от назначения кандидата 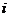на должность 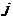оценивается как 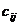. Необходимо так назначить кандидатов на должности, чтобы максимизировать общий эффект

.

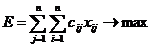Очевидно, что один кандидат может быть назначен только на одну должность. Это обстоятельство может быть формализовано в виде ограничений

, .

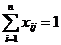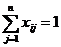Поскольку кандидат может быть или назначен, или не назначен на соответствующую должность, имеет место еще одно ограничение 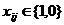. Решение задачи есть квадратная матрица с единичными элементами.

Транспортная задачаоптимизирует перевозки между несколькими пунктами отправки и получения груза. Пусть существует 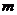пунктов отправки грузов, в каждом их которых имеется груз 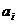. Их надо доставить 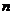получателям в объеме 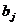. Здесь 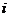и 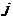номера пунктов отправления и получения груза. Затраты на перевозку груза из пункта 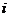в пункт 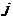определяются как 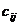. Необходимо составить оптимальный план перевозки так, чтобы

.

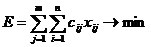Если предположить, что все грузы должны быть перевезены, то ограничения задачи имеют вид

.

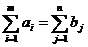
Решением задачи является матрица размерностью 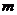на 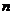элементов 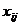, каждый из которых имеет смысл объема перевозки из пункта 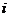в пункт .

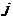Задача составления смесейвнешне похожа на задачу распределения ресурсов. Смысл задачи – минимизировать затраты на изготовление смеси различных веществ, например, при изготовлении бетона, так, чтобы при этом гарантировать наличие в смеси определенных составляющих, например, цемента, в заданном количестве. Тогда выражение для целевой функции имеет вид

.

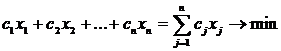Выражения для ограничений приобретают вид

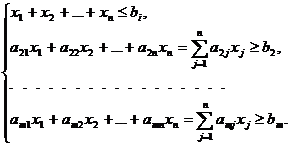
Здесь первое неравенство задает общий объем смеси, а выполнение остальных гарантирует наличие в ней принципиально необходимых компонентов в заданном количестве.

Задача о ранцепредусматривает выбор из имеющегося набора предметов. Предположим, что имеется 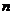видов предметов, а ценность каждого определяется коэффициентом 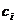. Каждый вид предметов имеет, например, объем 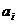. Из общего количества предметов необходимо выбрать такой набор, чтобы максимизировать его ценность

,

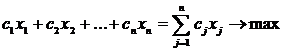при этом общий объем предметов не должен превысить некоторой величины предельного объема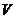

.

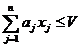Решение задачи позволяет оптимальным способом приблизить отобранный набор к заданному объему обеспечивая максимальную ценность выборки. Отметим, что если количество предметов какого-то вида ограничено, то это обстоятельство можно учесть, добавив в задачу ограничение вида 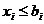.