Лабораторная работа №1. Методы поиска экстремумов с помощью надстройки Поиск решения пакета Excel

Задание

Установите у себя на машине надстройку Поиск решения и научитесь решать задачи поиска экстремума с ее помощью.

Порядок выполнения работы

1. Создайте новую рабочую книгу Excel.

2. Убедитесь, что в вашей рабочей книге в пункте главного меню Сервисимеется пункт Поиск решения (рис. 5). Если он отсутствует, то выберите пункт меню Сервис / Надстройки и в открывшемся окне включите режим Поиск решения (рис. 6). Если и в этом окне пункт Поиск решения отсутствует, то это означает, что на вашей машине установлена сокращенная версия электронных таблиц, поэтому произведите установку пакета Excel заново.

3. Возьмите в качестве основы для решения задачу линейного программирования (1, 2). Для задания значений параметров используйте (4). Задайтесь количеством неизвестных вашей задачи 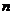и выделите на рабочем листе Excel группу смежных ячеек для хранения 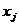. Обнулите эти ячейки.

4. Выберите на рабочем листе группу свободных смежных ячеек для хранения коэффициентов 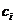. Задайтесь значениями коэффициентов 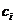из (4) и занесите их в соответствующие ячейки.

5. Выберите на рабочем листе свободную ячейку для хранения результатов вычисления целевой функции (1). Воспользовавшись функцией СУММПРОИЗВ(), запрограммируйте в выбранной ячейке формулу для вычисления значения целевой функции. Меняя данные в ячейках 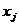, убедитесь в правильности прогаммирования целевой функции.

6. Выберите на рабочем листе группу смежных ячеек для хранения коэффициентов 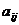. Задайтесь значениями коэффициентов 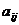из (4) и занесите их в соответствующие ячейки.

7. Выделите на рабочем листе группу свободных смежных ячеек для хранения коэффициентов 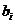. Задайтесь значениями коэффициентов 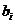из (4) и занесите их в соответствующие ячейки.

8. Выберите на рабочем листе группу свободных смежных ячеек для хранения результатов вычисления сумм

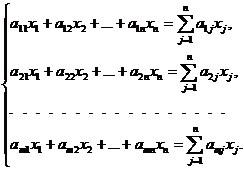(5).

9. Воспользовавшись функцией СУММПРОИЗВ(), рассчитайте в выбранных вами ячейках значения (5). Меняя данные в ячейках 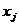, убедитесь в правильности вычисления (5).

10. Выполните команду Сервис / Надстройки / Поиск решения и в открывшейся форме Поиск решения в поле Установить целевую ячейку укажите ячейку, в которой рассчитывается целевая функция (см. шаг 5). В окне Изменяя ячейки укажите область, в которой размещены управляемые переменные 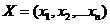(см. шаг 3). В поле Ограничения нажмите кнопку Добавить, и в открывшейся форме Добавление ограничений в поле Ссылка на ячейку укажите адреса ячеек, созданных на шагах 8 и 9. В среднем окне задайте вид ограничения. В окно Ограничения занесите адреса ячеек, в которых размещаются коэффициенты 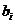(см. шаг 7). Закройте форму Добавление ограничений и убедитесь, что введенные вами ограничения появились в области Ограниченияна панели Поиск решения.

11. Нажмите кнопку Параметры и перейдите к форме Параметры поиска решения. Ознакомьтесь с настройками параметров по умолчанию. Установите флажок Неотрицательные значения. Установите другие значения параметров по своему усмотрению. Вернитесь в окно Поиск решения.

12. Нажмите кнопку Выполнить и получите результат работы надстройки. Если вы получаете диагностическое сообщение Решение найдено. Все ограничения и условия оптимальности выполнены, то закажите все предлагаемые отчеты. Ознакомьтесь с их содержанием и убедитесь, что результаты вычислений совпадают с результатами, представленными на рис. 13, 14, 15. Если вы получаете другое диагностическое сообщение или другие результаты оптимизации, то ищите ошибку программирования надстройки Поиск решения или задания исходных данных и повторите решение задачи и генерацию отчетов.

13. По согласованию с преподавателем выберите себе из таблицы 2 индивидуальное задание на вычисление экстремума. Выполните программирование и получите решение. Убедитесь, что вычисленное вами значение целевой ячейки совпадает со значением 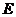, указанным в таблице 2. Ознакомьтесь с отчетами, генерируемыми системой.

14. Вернитесь к программируемой задаче. На панели Поиск решения в поле Ограничениянажмите кнопку Изменить и на форме Добавление ограничений для выбранных вами параметров задайте дополнительное ограничение Целое. Сравните первоначальные результаты работы и результаты в работы в целочисленном режиме.

Контрольные вопросы

1. Какие методы поиска экстремумов существуют?

2. Почему при решении задачи Канторовича нельзя воспользоваться методом Ньютона?

3. Что такое целевая функция?

4. В чем разница между линейными и нелинейными задачами?

5. Почему количество ограничений задачи не связано с количеством ее переменных?

6. Каково назначение надстройки Поиск решения?

7. Какой смысл флажка Неотрицательные значенияформы Параметры поиска решения?

8. Какой смысл флажка Линейная модельформы Параметры поиска решения?

9. Какой смысл параметра ограниченияЦелое?

10. Что означает статус Связанное в отчете по результатам?

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, пример результатов вычислений экстремума, результаты решения индивидуального задания из таблицы 2, результаты исследования решения задачи в зависимости от различных вариантов установки ограничения Целое. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Вариант титульного листа отчета, какой он был в 2007-2008 учебном году, приведен в приложении А. С действующим вариантом титульного листа можно ознакомиться на http://standarts.guap.ru

Таблица 2. Индивидуальные задания на вычисление экстремумов функций.

Вариант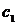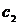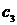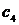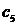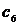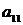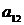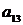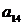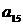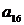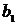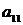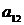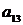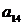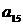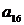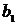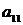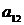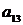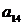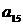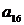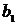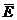
	7,5	20,7	25,2	48,7	43,1	58,6	38,2	10,1	59,6	89,9	88,5	95,8	478,7	35,0	51,3	59,7	61,7	27,1	9,3	716,2	29,7	87,0	87,5	91,4	46,8	79,5	643,8	338,3
	76,5	51,9	15,3	6,1	45,7	57,5	1,5	40,7	86,3	13,9	24,5	4,5	347,0	0,2	47,3	97,9	65,4	70,4	87,0	472,8	34,4	9,7	15,3	0,3	2,1	90,7	888,2	2263,5
	18,7	51,5	8,9	0,9	69,4	37,2	3,2	16,4	22,0	1,7	28,5	34,3	414,4	30,5	5,2	61,0	16,9	42,1	49,6	288,7	99,6	28,4	86,4	95,7	18,3	49,6	774,8	1306,0
	42,3	6,2	6,6	41,7	57,3	60,8	55,4	35,7	37,2	35,6	91,0	46,6	778,5	41,8	79,4	97,9	75,8	11,3	39,6	599,2	55,7	94,5	87,4	90,0	60,3	99,1	962,5	696,2
	77,5	31,9	15,7	14,2	6,3	76,7	42,6	30,4	97,6	80,7	99,1	25,6	737,3	73,8	93,1	81,8	89,0	57,5	0,3	848,1	31,4	43,8	62,8	35,8	80,1	47,1	237,8	587,3
	34,0	83,8	19,8	51,1	1,0	94,6	95,2	5,3	70,5	81,7	97,3	46,6	959,0	19,9	89,4	30,6	3,8	4,6	59,4	696,6	29,4	33,5	14,6	0,9	72,4	57,6	255,3	1187,7
	88,0	95,8	50,5	11,3	3,4	17,4	30,0	75,0	35,1	77,6	7,4	19,8	744,9	20,1	23,9	20,6	57,5	61,6	68,1	456,6	80,2	97,1	86,5	66,0	29,2	49,2	95,6	105,0
	77,6	42,6	68,2	66,0	51,3	50,5	6,4	35,8	48,7	51,1	37,3	98,6	297,3	51,5	65,1	64,6	98,5	89,3	21,1	485,4	66,3	16,5	12,5	83,3	49,0	2,7	126,0	469,3
	37,4	47,3	18,9	3,0	47,6	1,2	4,1	23,1	0,5	92,6	10,0	25,7	620,5	19,6	73,0	24,3	12,8	37,9	86,3	294,2	82,7	89,4	70,6	48,2	25,9	89,1	190,5	350,3
	70,5	67,4	4,7	17,4	73,7	83,7	77,6	68,0	80,9	72,4	8,5	13,2	77,9	33,5	75,5	66,4	91,1	30,4	3,6	216,8	76,7	35,2	87,6	20,4	79,7	96,8	600,0	557,1
	89,6	46,3	35,7	62,0	95,7	29,7	75,6	62,7	17,4	40,5	55,2	71,2	818,5	65,1	25,9	94,2	27,6	90,5	27,9	798,1	7,9	94,6	1,3	51,1	32,0	27,0	853,8	1300,8
	60,6	17,2	22,1	20,8	43,5	70,1	55,5	18,1	97,0	68,7	52,9	79,7	576,3	41,8	58,4	74,0	60,5	60,4	53,2	319,6	92,4	5,0	11,6	95,7	69,7	5,8	274,2	436,3
	61,5	55,3	0,4	48,7	65,6	86,4	80,6	26,2	17,8	86,7	11,5	6,0	911,3	37,0	31,2	64,8	6,1	31,5	29,6	523,2	62,5	30,6	60,9	68,3	94,9	86,1	82,2	148,9
	71,4	16,8	46,2	57,9	30,5	55,9	76,2	73,8	98,6	92,6	90,4	54,5	941,5	95,8	15,8	50,2	63,8	24,4	34,1	415,9	98,5	57,3	80,2	1,6	52,2	50,6	105,5	425,2
	92,9	70,8	97,6	83,9	8,7	51,4	50,1	67,5	49,0	14,6	3,8	79,6	663,1	92,0	21,8	78,9	48,3	28,7	37,9	302,5	72,8	0,9	42,0	63,7	48,9	35,4	226,4	835,7
	57,3	46,2	34,5	97,1	5,9	26,5	67,2	73,2	58,5	15,2	89,2	37,8	809,5	59,0	0,6	58,9	90,9	54,0	97,1	221,2	21,5	62,7	81,6	23,5	72,0	42,9	193,6	335,5
	78,5	99,3	38,8	77,0	16,2	44,8	20,0	20,6	33,4	32,5	30,0	80,2	694,1	93,1	12,7	29,0	10,5	58,6	35,1	410,8	15,4	89,6	99,0	3,6	56,2	55,0	96,3	1688,8
	18,8	76,8	65,8	50,0	38,3	23,4	69,6	27,1	90,4	3,9	70,9	45,4	796,5	96,5	28,8	65,9	54,0	37,7	53,2	461,6	70,4	94,6	43,4	85,1	88,4	63,9	91,8	139,2
	96,3	61,5	59,0	30,9	88,2	44,9	51,7	25,7	29,1	80,2	78,9	67,6	536,2	26,7	37,2	89,6	99,2	64,1	56,3	581,2	19,0	45,3	34,5	85,3	58,6	68,4	144,8	735,6
	88,2	23,4	24,5	24,7	14,8	84,4	75,5	94,9	61,9	72,2	96,8	36,9	728,6	64,0	2,7	6,5	68,4	13,3	85,3	515,8	78,7	91,8	82,2	87,6	94,3	95,6	917,6	744,6
	30,1	37,3	39,8	75,7	80,4	75,4	85,0	55,7	87,3	44,1	21,8	85,9	760,4	4,3	27,9	8,7	81,1	61,2	54,6	4,9	7,2	37,3	67,3	21,3	62,4	75,2	153,1	34,4
	28,9	4,5	68,1	48,1	74,1	59,2	28,0	70,3	70,7	37,6	33,0	8,6	808,3	47,2	79,0	20,4	38,0	52,2	83,2	638,4	42,7	30,0	26,5	28,8	97,0	63,9	237,5	610,7
	77,9	2,6	82,2	35,7	92,8	32,1	97,7	28,6	53,4	40,7	99,8	89,5	823,6	96,7	4,4	84,1	44,1	93,6	26,3	995,2	7,3	20,0	78,3	88,7	28,0	69,3	753,5	981,7
	88,5	79,0	28,8	65,2	74,1	6,4	81,1	90,9	57,5	70,6	40,1	11,1	32,5	25,4	65,0	98,6	0,6	57,5	35,2	973,7	4,4	61,5	35,0	34,9	59,9	3,1	971,9	60,0
	51,9	77,9	15,2	29,1	57,2	57,0	89,7	38,6	9,6	77,8	78,4	66,6	945,7	94,7	75,6	93,0	94,0	80,8	53,4	932,2	93,5	87,7	81,5	2,7	86,6	77,3	296,8	460,6

Примечание. Для всех ограничений предполагается знак 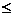. Сами оптимальные решения 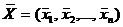не представлены. Для контроля правильности ваших вычислений используйте значение целевой функции .

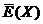Теория принятия решений

Основные понятия теории принятия решений

В основе теории принятия решений лежит понятие проблемы. Большая Советская Энциклопедия (БСЭ) дает следующее определение понятия проблема: «Проблема (от греч. рroblema – задача), в широком смысле сложный теоретический или практический вопрос, требующий изучения, разрешения, в науке – противоречивая ситуация, выступающая в виде противоположных позиций в объяснении каких либо явлений, объектов, процессов и требующая адекватной теории для их разрешения. Важной предпосылкой успешного решения проблемы служит ее правильная постановка. Неверно поставленная проблема или псевдопроблема уводит в сторону от решения подлинных проблем».

В учебнике по разработке управленческих решений [2] дается с одной стороны более узкое, а с другой стороны более точное определение этого понятия: «Проблема - понятие, характеризующее разницу между действительным и желаемым состоянием объекта». Применительно к задачам нашего изложения мы рассматриваем понятие проблемы в следующем виде: проблема - субъективно сформулированное описание ситуации, в которой имеется расхождение между действительным и желаемым состоянием объекта и разрешение которой позволяет получить некий эффект

При разрешении проблемы преследуется некая цель. Цель ‑ это один из элементов поведения и сознательной деятельности человека, который характеризует предвосхищение в мышлении результата деятельности и пути его реализации с помощью определенных средств. Цель выступает как способ интеграции различных действий человека в некоторую последовательность или систему. Анализ деятельности как целенаправленной предполагает выявление несоответствия между наличной жизненной ситуацией и целью, то есть выявление проблемы. Достижение цели является процессом преодоления этого несоответствия и разрешения проблемы с получением эффекта.

Предполагается, что цель или цели недвусмысленно сформулированы, имеют сроки исполнения, мотивируют действия исполнителя в необходимом направлении и совместимы с интересами организации и отдельных групп исполнителей. Официальные цели определяют общее назначение организации, декларируются в уставе, а также заявляются публично руководителем. Они объясняют необходимость организации для общества, имеют внешнюю направленность и выполняют важную защитную функцию, создавая организации соответствующий имидж. Оперативные цели определяют, чем на самом деле в текущий период занимается организация, и могут не полностью совпадать с официальными целями. Такие цели имеют внутреннюю направленность и призваны мобилизовать ресурсы организации. Формой их выражения может быть план работы.

Операционные цели еще более конкретны и измеряемы. Они направляют деятельность конкретных работников и позволяют давать оценку их работе. Такие цели формулируются в виде конкретных заданий отдельным группам и исполнителям. Именно операционные цели легче всего формализуются и их достижение точнее всего фиксируется. В соответствии с БСЭ «операция (от лат. оperatio – действие), 1)законченное действие или ряд действий, направленное на решение определенной задачи, достижение поставленной цели, … 2)очередное периодически повторяющееся действие, входящее в круг функций, задач данного учреждения, предприятия или их отдела …».

Степень достижения цели операции удобно измерять критерием. По определению БСЭ «критерий (от греч. kriterion – средство для суждения), признак, на основании которого производится оценка, определение или классификация чего-либо; мерило суждения, оценки». Существуют и другие, более точные определения критерия. Так, в соответствии с [3], «критерием называется математическое выражение цели». Еще одно определение дается в книге [4]: «под критерием будем понимать некоторую функцию от состояния системы, отражающую цели функционирования системы в каждый определенный отрезок времени». Фактически критерий представляет собой некую математическую функцию, в том числе и функцию времени, значения которой могут быть вычислены. Очевидно, что далеко не для каждой цели можно подобрать математический критерий. С другой стороны, если такой критерий существует, то его величина характеризует степень достижения этой самой цели.

В теории принятия решений принято оперировать так называемыми альтернативами. По определению БСЭ «альтернатива (от лат. alter – один из двух), ситуация, в которой надлежит произвести выбор одной из двух исключающих друг друга возможностей (эти возможности также нередко называются альтернативами) …». Тем не менее, количество альтернатив может быть и большим двух. Обычно в теории принятий решений оперируют таким определением: «Альтернатива - вариант решения задачи разработки управленческого решения». Таких вариантов может быть два, несколько или бесконечное количество. Таким образом, под решением понимается выбор альтернативы. С другой стороны, если альтернатива одна, то решение принимать не надо, поскольку выбор отсутствует.

Выбор альтернативы можно производить по самым разным правилам. Наибольший интерес представляет альтернатива, которая обеспечивает наилучшее значение критерия. Очевидно, что это решение соответствует максимуму или минимуму критериальной функции. Для обозначения такого решения обычно используют термин оптимальное. В соответствии с БСЭ «оптимальный (от лат. optimus- наилучший), наиболее благоприятный, лучший из возможных (напр., О. решение)». Тогда оптимальное решение- альтернатива, которая обеспечивает максимум критерия (критериальной функции) из числа всех возможных. Факт существования оптимального решения надо доказать. Это можно сделать, например, воспользовавшись ранее рассмотренными методами поиска экстремумов функций.

Оптимальные решения на практике достаточно редки. Это объясняется в первую очередь объективными сложностями записи выражений критериальных функций как функций аргументов и параметров решаемой задачи. В некоторых случаях это сделать просто невозможно, а в некоторых возникают проблемы с решением задачи поиска экстремума. Поэтому достаточно часто практики сталкиваются с необходимостью выбора из конечного набора альтернатив, полученных самыми разными способами. Делать этот выбор можно разными методами. Наиболее логичным и разумным представляется выбор той альтернативы из числа имеющихся, которая обеспечивает наилучшее значение критериальной функции.

В соответствии с БСЭ «рационализм (франц. rationalisme, от лат. ratkmalis - разумный, ratio - разум), филос. направление, признающее разум основой познания и поведения людей». Если делается разумный выбор, то возникает так называемое рациональное решение- альтернатива, которая обеспечивает максимум критерия (критериальной функции) из числа всех найденных. В отличие от оптимального решения, рациональное решение может быть улучшено, если каким-либо способом будет найдена альтернатива, обеспечивающая лучшее значение критериальной функции.

Кроме рационального может существовать еще большое количество других методов выбора вариантов решений. Очевидно, что любой отличный от рационального метод выбора альтернативы не может обеспечить значение критериальной функции лучшее, чем имеет место при рациональном и, тем более, оптимальном решении. Мотивы, побуждающие людей делать нерациональный выбор, могут быть самыми разными. Не вдаваясь в детали, будем называть нерациональные решения случайными.