Методы поиска экстремумов функций

Экстремумомфункции 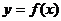на интервале 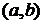называется наибольшее или наименьшее значение функции относительно некоторой окрестности. Это значение может отличаться от наибольшего или наименьшего значения на всей области определения. Найти экстремум 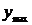– это значит найти такое значение аргумента 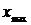, при котором функция имеет максимум или минимум (рис. 2).

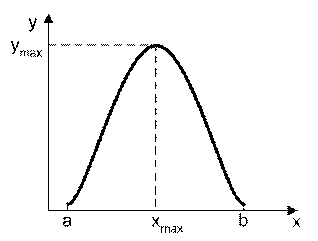
Рис. 2. Экстремум функции на интервале определения

Традиционным методом поиска экстремума является дифференциальное исчисление(метод И. Ньютона). Необходимым условием существования экстремума дифференцируемой на интервале функции является равенство нулю первой ее производной. Соответствующая точка рассматривается как критическая. Достаточным условием существования максимума дифференцируемой на интервале функции является отрицательное значение второй производной функции в критической точке, а минимума - положительное значение второй производной. Если вторая производная в рассматриваемой точке равна нулю, то экстремум не существует, а критическая точка является точкой перегиба.

Предположим, что функция изменяет свое значение на интервале определения 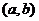, но имеет экстремум вне интервала. Тогда возникает задача поиска находящихся как раз на границах интервала максимального и минимального значения функции (рис. 3). Отметим, что первая производная функции на границах интервала определения в этом случае вовсе не обращается в нуль. Поэтому использование традиционного метода поиска экстремума (метода И. Ньютона) в данном случае оказывается невозможным.

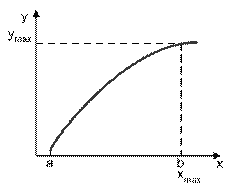
Рис. 3. Экстремум на границе интервала определения

Функция нескольких переменных 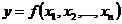также может быть дифференцируема в некой точке (полный дифференциал). Если функция дифференцируема в некой точке, то существуют частные производные по каждой из переменных, причем в критической точке они обращаются в нуль 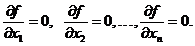(обратное не верно). В зависимости от конкретного вида функции 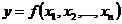таких точек может быть ни одной, одна или несколько. Существование критической точки является необходимым, но не достаточным условием экстремума. Для его нахождения необходимо вычислить вторые чистые и смешанные производные критериальной функции

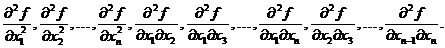
Производная в некой точке по направлению может рассматриваться как производная сечения многомерной функции плоскостью, образованной направлением и точкой. Вектор производных функции по каждой из координат в некой точке называется градиентом функции в заданной точке, а сам метод поиска экстремумов градиентным.

Достаточное условие существования локального экстремума формулируется следующим образом [15]: пусть функция 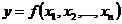имеет критическую точку ( 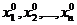), определяемую за счет вычисления выражений

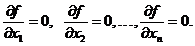
Тогда, если дифференциал второго порядка

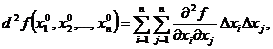
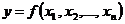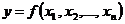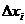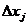больше нуля, то функция имеет минимум, а если меньше нуля, то функция имеет максимум при любых и , не обращающихся в нуль одновременно. Если в зависимости от 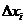и 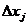значение дифференциала может принимать и положительные, и отрицательные значения, то экстремума в критической точке нет.

Если функция 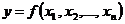имеет несколько экстремумов, то их обычно называют локальными. Наибольший их локальных максимумов или наименьший из локальных минимумов называют глобальным.

В качестве примера рассмотрим функцию двух переменных 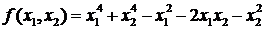. Приравняем к нулю ее первые частные производные

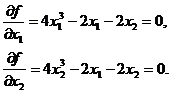
Вычитая из первого уравнения второе, имеем 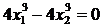, откуда 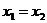. Подставляя 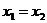в выражения для частных производных, имеем 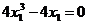. Получившееся уравнение имеет три решения: 0, 1, -1. Тогда критическими точками являются 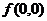, 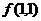и .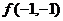

Вторые частные производные имеет вид

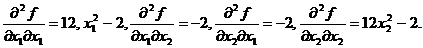
Следуя [6], «разумным» образом выберем комбинацию приращени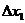й и 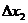равными +1 и –1, поскольку такие значения соответствуют максимально возможному диапазону изменения аргументов при переходе от одной критической точки к другой. Результаты вычислений вторых частных производных и дифференциала второго порядка при различных комбинациях 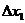и 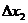сведены в таблицу 1.

Как следует из таблицы 1, в критической точке (0,0) локального экстремума нет. А вот в точках (1,1) и (-1,-1) имеют место локальные минимумы. Поскольку в рассматриваемом примере значения критериальной функции в точках (1,1) и (-1,-1) равны между собой, в качестве оптимального решения можно выбрать любое из двух предложенных.

Таблица 1. Расчеты критических точек

Критическая точка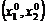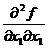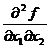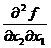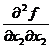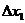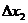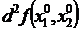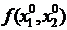
(0,0)	-2	-2	-2	-2	-1 -1	-1 -1	-8
(1,1) (-1,-1)		-2	-2		-1 -1	-1 -1		-2