Средняя величина остатков не равна нулю

остатки гетероскедастичны

остатки автокоррелированны

дисперсия остатков не является постоянной величиной

Решение:

Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений 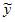минимальна. Отклонение 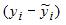, посчитанное для i-го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю.

5. Пусть y – издержки производства, 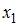– объем продукции, 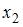– основные производственные фонды, 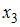– численность работников. Известно, что в уравнении 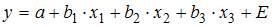дисперсии остатков пропорциональны квадрату объема продукции .

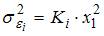Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на 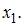После применения обобщенного метода наименьших квадратов новая модель приняла вид 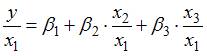. Тогда параметр 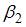в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …

Фондоемкости продукции при неизменном уровне трудоемкости продукции

трудоемкости продукции при неизменном уровне фондоемкости продукции

фондовооруженности труда при неизменном уровне производительности труда производительности труда при неизменном уровне фондовооруженности труда

Решение:

Пусть y – издержки производства, 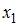– объем продукции, 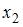– основные производственные фонды, 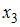– численность работников. Известно, что в уравнении 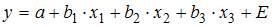дисперсии остатков пропорциональны квадрату объема продукции .

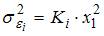После применения обобщенного метода наименьших квадратов новая модель приняла вид 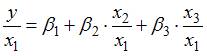. Новая модель имеет дело с новыми переменными 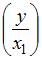– затраты на единицу продукции, 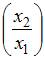– фондоемкость продукции, 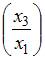– трудоемкость продукции. В новой модели параметр 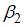показывает среднее изменение затрат на единицу продукции 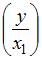с увеличением на единицу фондоемкости продукции 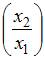при неизменном уровне трудоемкости продукции .

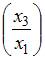Тема 9: Оценка тесноты связи

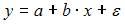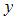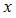1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …

Корреляции

детерминации

регрессии

эластичности

Решение:

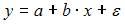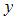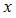Заданная регрессионная модель вида – это линейное уравнение парной регрессии, для которого показателем тесноты связи между переменными и является парный коэффициент линейной корреляции.

2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 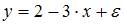является …

[–1; 0]

[0; 1]

[–1; 1]

[–2; 2]

Решение:

Коэффициент корреляции для парной линейной регрессии в общем случае изменяется в пределах [–1, 1]. Однако так как значение коэффициента регрессии отрицательное, то и значение коэффициента корреляции для уравнения тоже будет отрицательным, значит, самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 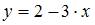будет [–1; 0].

3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии 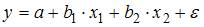, если известны парные коэффициенты корреляции 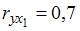, 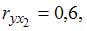является интервал …

[0,7; 1]

[0; 1]

[0,6; 0,7]

[-1; 1]

Решение:

Показатель множественной корреляции изменяется в пределах [0; 1]. Однако величина индекса множественной корреляции должна быть больше максимального парного индекса корреляции или равна ему 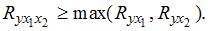Следовательно, самым коротким интервалом изменения показателя множественной корреляции будет [0,7; 1].

4. Для регрессионной модели вида 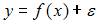получена диаграмма

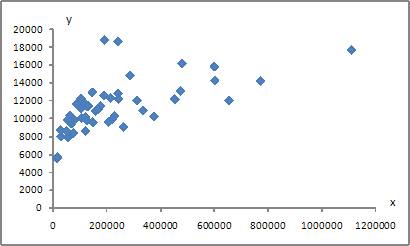
Такое графическое отображение называется …

Полем корреляции

диаграммой детерминации

полем детерминации

коррелограммой

Решение:

Графическое отображение совокупности точек с координатами 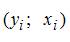на плоскости для зависимости от называется полем корреляции, или диаграммой рассеяния. Поэтому верный ответ – «полем корреляции».