Тема 2: Отбор факторов, включаемых в модель множественной регрессии

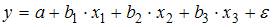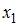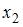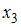1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы 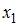, 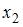и …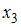

Независимы

мультиколлинеарны

количественно измеримы

значимы

Решение:

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 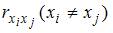были бы равны нулю.
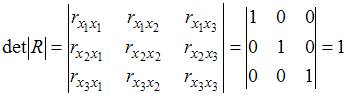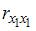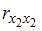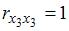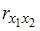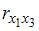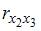, поскольку = = и = = =0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.

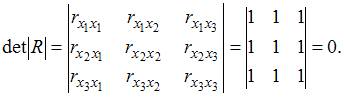
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

2. При моделировании линейного уравнения множественной регрессии вида 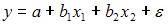необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

x₁ и x₂

y и {x₁; x₂}

a и {b₁; b₂}

b₁ и b₂

Решение:

Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 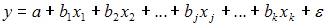, где y – зависимая переменная; x_j – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, b_j – параметры (a – свободный член уравнения, b_j – коэффициент регрессии); 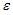– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x₁ и x₂.

Дана матрица парных коэффициентов корреляции.

Коллинеарными являются факторы …

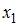и

и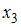

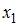и

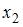
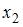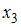
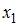и y

Решение:

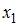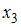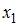Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если . В нашей модели только коэффициент парной линейной регрессии между факторами и больше 0,7. , значит, факторы и 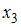коллинеарны.

4. В модели множественной регрессии 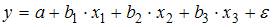определитель матрицы парных коэффициентов корреляции между факторам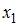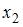и , и 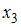близок к нулю. Это означает, что факторы 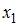, 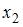и …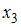

Мультиколлинеарны

независимы

количественно измеримы

значимы

Решение:

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 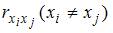были бы равны нулю.
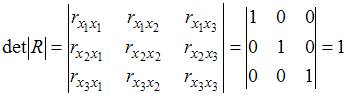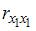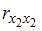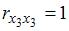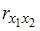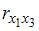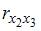, поскольку = = и = = =0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.

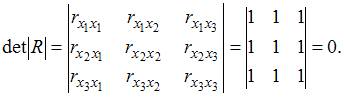
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

5. Для эконометрической модели линейного уравнения множественной регрессии вида 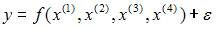построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х⁽¹⁾, х⁽²⁾, х⁽³⁾, x⁽⁴⁾– независимые переменные):

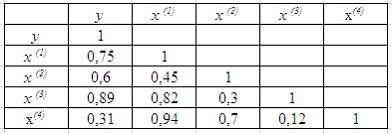
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …

x⁽²⁾ и x⁽³⁾

x⁽¹⁾ и x⁽³⁾

x⁽¹⁾ и x⁽⁴⁾

x⁽²⁾ и x⁽⁴⁾

Решение:

При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары независимых (объясняющих) переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными (теснота связи с переменной y в данном случае не рассматривается). Такие независимые переменные называются коллинеарными. Если значение коэффициента парной корреляции между объясняющими переменными не превышает по абсолютной величине 0,7, то такие объясняющие переменные не являются коллинеарными. Рассмотрим значения парных коэффициентов межфакторной корреляции: между x⁽¹⁾ и x⁽²⁾ значение равно 0,45; между x⁽¹⁾ и x⁽³⁾ – равно 0,82; между x⁽¹⁾ и x⁽⁴⁾ – равно 0,94; между x⁽²⁾ и x⁽³⁾ – равно 0,3; между x⁽²⁾ и x⁽⁴⁾ – равно 0,7; между x⁽³⁾ и x⁽⁴⁾ – равно 0,12. Таким образом, не превышают 0,7 значения 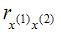, , 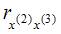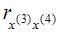. Следовательно, коллинеарными не являютсяфакторы x⁽¹⁾ и x⁽²⁾, x⁽²⁾ и x⁽³⁾, x⁽³⁾ и x⁽⁴⁾. Из последних перечисленных пар в вариантах ответов присутствует пара x⁽²⁾ и x⁽³⁾ – это верный вариант ответа. Для остальных пар: x⁽¹ и x⁽³⁾, x⁽¹⁾ и x⁽⁴⁾, x⁽²⁾ и x⁽⁴⁾ – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.

Тема 3: Фиктивные переменные

1. Дана таблица исходных данных для построения эконометрической регрессионной модели:

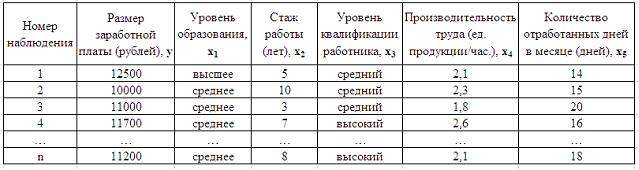Фиктивными переменными не являются …

стаж работы

производительность труда

уровень образования