Выборочные средние значения компонент

, ;

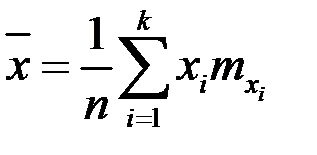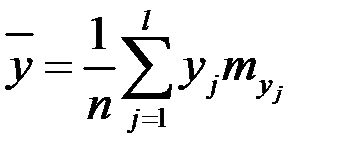Выборочные дисперсии компонент

,

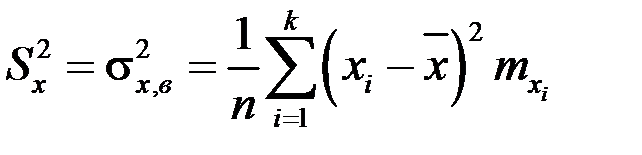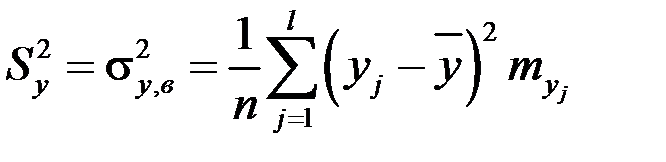
или

, ;

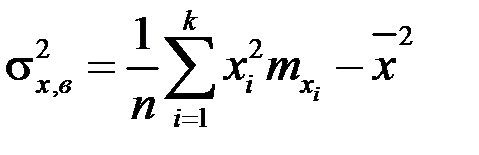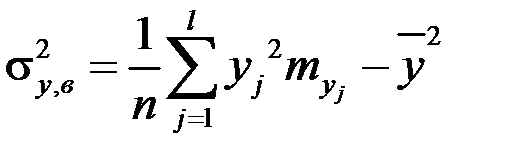Выборочный корреляционный момент

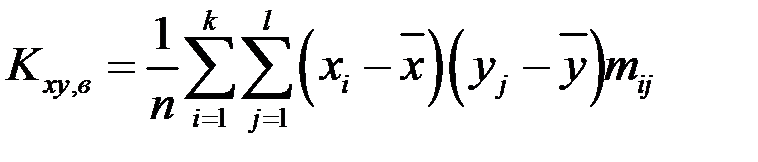
или

;

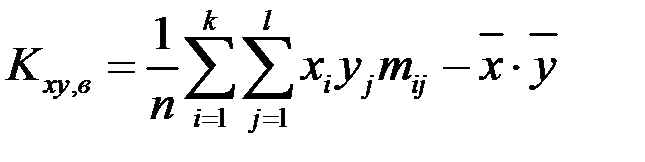Выборочный коэффициент корреляции

;

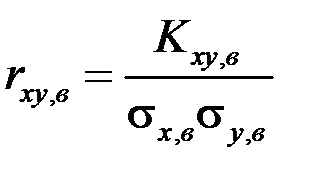Условные средние компонент

, ,

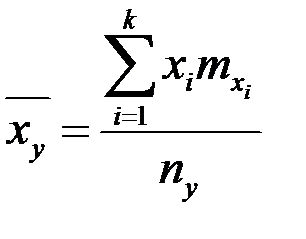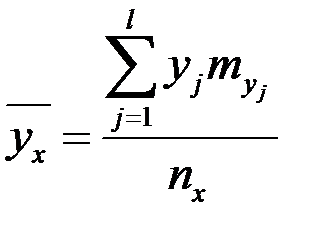где усреднение ведется в 1-ой формуле лишь по тем 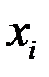, которые появились совместно с данным у, а во 2-ой формуле лишь по тем 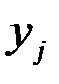, которые появились совместно с данным х.

Функция регрессии имеет важное значение при статистическом анализе зависимостей и может быть использована для прогнозирования значений одной из СВ, если известны значения другой СВ. Точность такого прогноза определяется условной дисперсией. Однако возможности практического применения функции регрессии весьма ограничены, так как для ее использования необходимо знать аналитический вид двумерного распределения 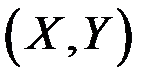. Поэтому идут на упрощение и вместо корреляционной зависимости рассматривают статистическую зависимость, которая устанавливает функциональную связь между значениями одной из величин и условным средним другой величины, например

,

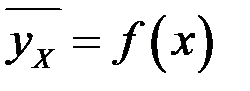эта функция называется эмпирической функцией регрессии, а ее график – эмпирической линией (кривой) регрессии. На практике получают лишь оценку кривой регрессии, так как число значений величины Х в выборке конечно.

Функция регрессии обладает замечательным свойством – она дает наименьшую среднюю погрешность оценки прогноза, т.е. величина

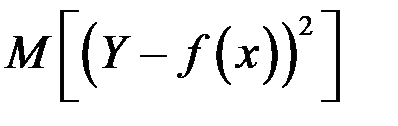
является минимальной именно для функции

.

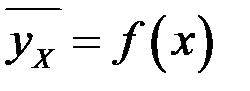На этом свойстве построен метод наименьших квадратов для определения неизвестных параметров функции регрессии.

Сущность метода наименьших квадратов состоит в выборе линии регрессии таким образом, чтобы сумма квадратов отклонений экспериментальных значений Y от теоретических была наименьшей.

Для иллюстрации метода рассмотрим частный случайлинейной регрессии

.

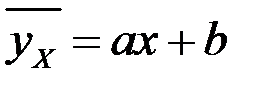По данным выборки требуется определить параметры а и b.

Строим функцию :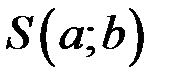

.

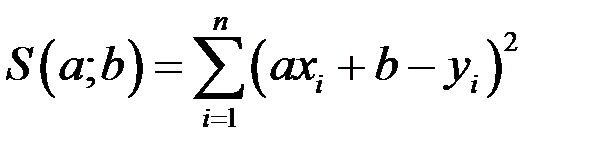Используя корреляционную таблицу функцию 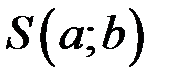можно записать в виде

.

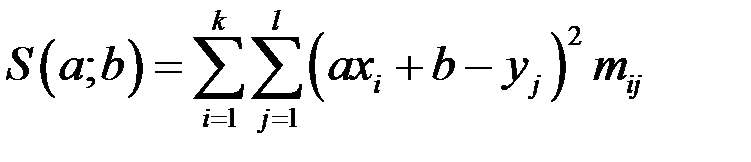Составляем необходимые условия экстремума:

.

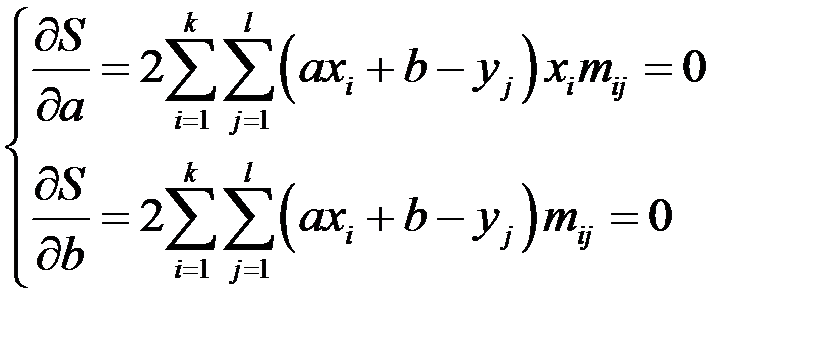После упрощения система примет вид:

.

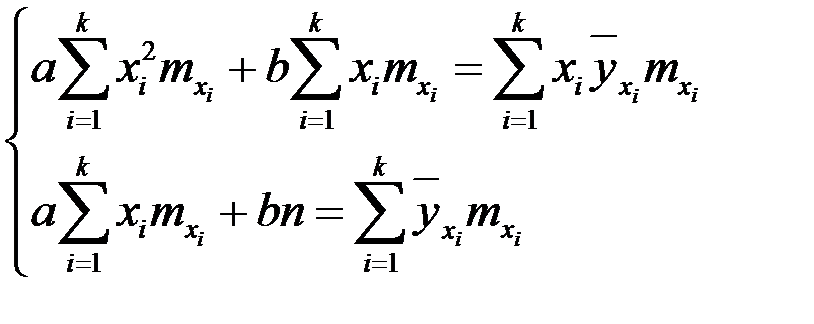Последнюю систему называютнормальной,решая ее получаем значения неизвестных коэффициентов а и b.

Уравнение регрессии можно также найти путем вычисления коэффициента регрессии. Уравнение регрессии у на х можно записать в виде

.

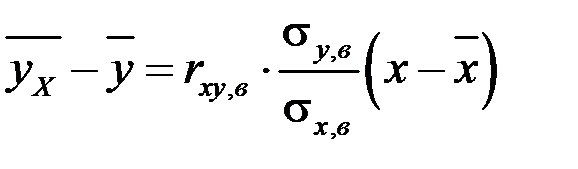Число 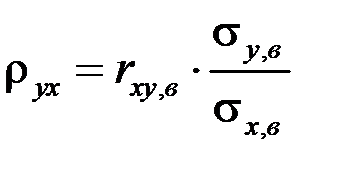называют коэффициентом регрессииу на х.

Пример

Двумерная выборка результатов совместных измерений признаков х и у объемом 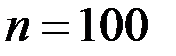измерений задана корреляционной таблицей:

Таблица 5

Y X		4,2	5,4	6,6	7,8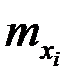
1,2			–	–	–
				–	–
4,8	–			–	–
6,6	–	–			–
8,4	–	–			–
10,2	–	–
	–	–	–

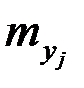1. Найти выборочные средние 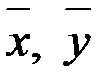и выборочные дисперсии .

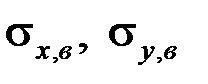2. Построить уравнение линии регрессии уна х в виде .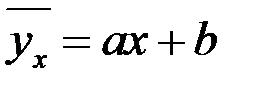

3. На графике изобразить корреляционное поле, т.е. нанести точки 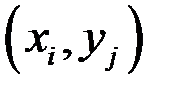и построить прямую .

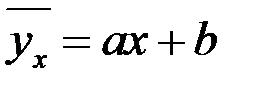Решение

1. Запишем законы распределения для случайных величин Х и Y:

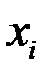	1,2		4,8	6,6	8,4	10,2

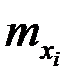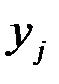		4,2	5,4	6,6	7,8

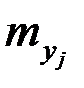Найдем числовые характеристики. Выборочные средние:

,

,

,

;

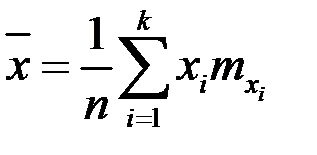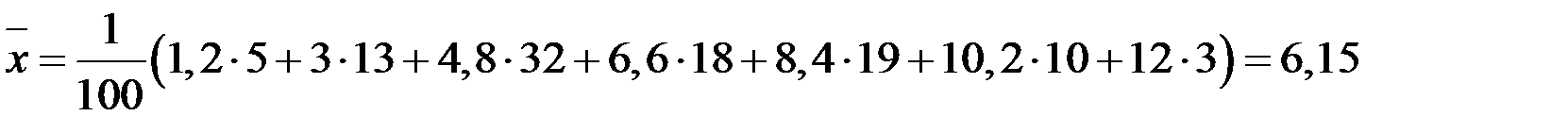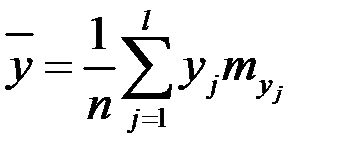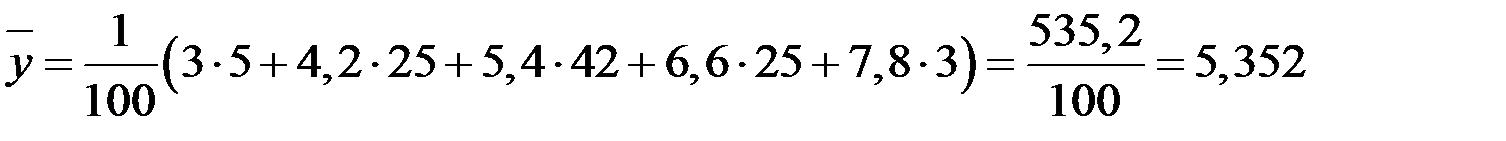выборочные дисперсии:

,

,

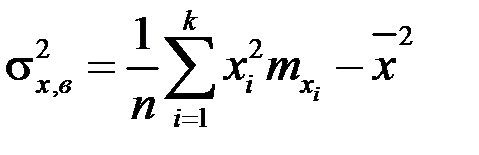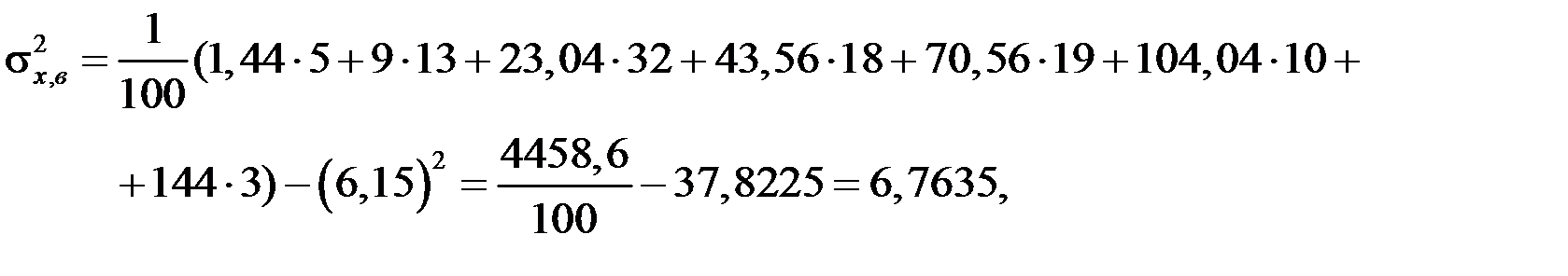
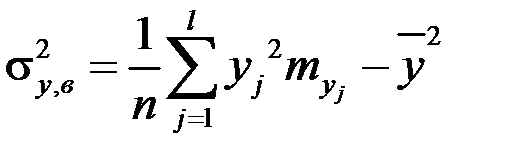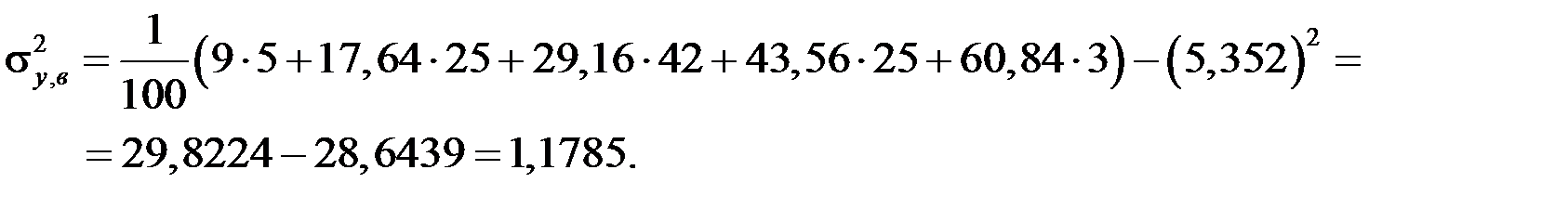
2. Найдем уравнение линии регрессии 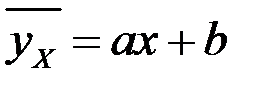у на х по методу наименьших квадратов, для этого составим систему уравнений для нахождения коэффициентов а и b:

,

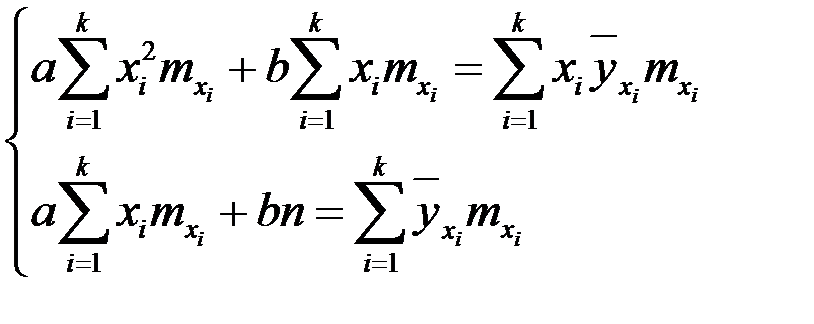выше при вычислении числовых характеристик было найдено:

, .

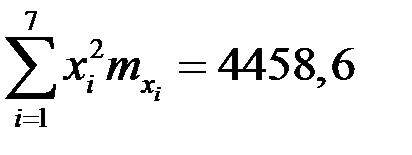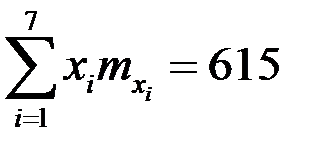Используя корреляционную таблицу каждому варианту 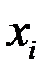признака Х поставим в соответствие среднее арифметическое 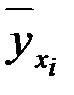соответствующих ему (входящих с ним в пару) значений признака Y, т.е.

,

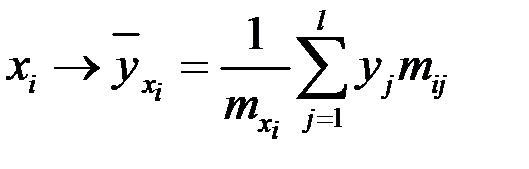результаты вычислений сведем в таблицу (таблица 6).

Таблица 6

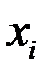	1,2		4,8	6,6	8,4	10,2
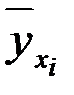	3,72	4,10769	4,875	5,9333	6,03157	6,36	7,4

Вычислим:

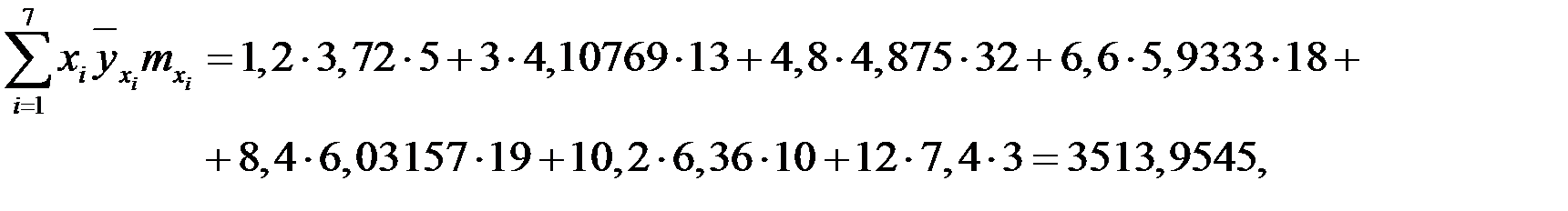
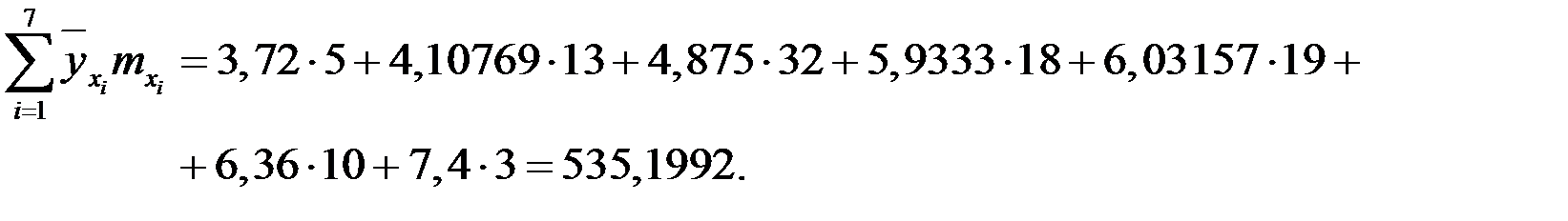
Подставим найденные коэффициенты и свободные члены в систему, получим

.

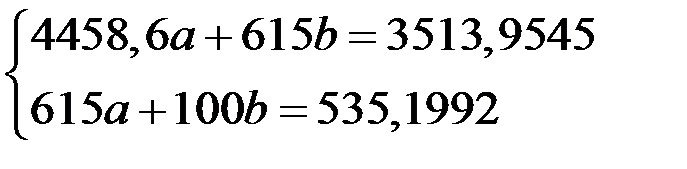Решим систему по формулам Крамера:

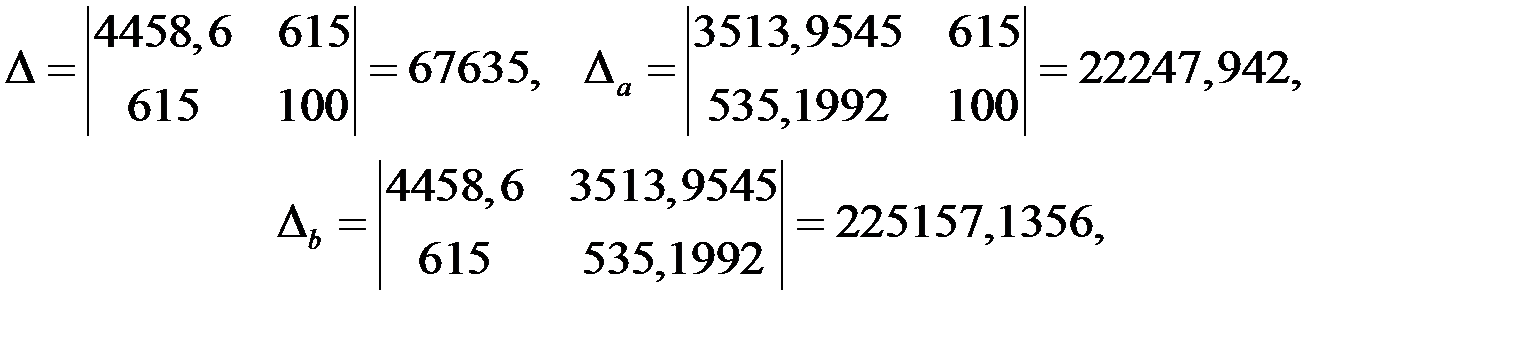
тогда

.

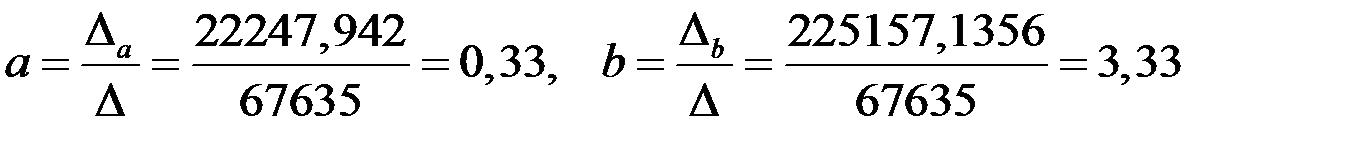Таким образом, эмпирическая функция регрессии у на х имеет вид:

.

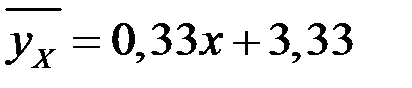Найдем ту же эмпирическую функцию регрессии у на х путем вычисления коэффициента регрессии

.

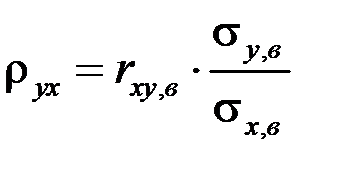Найдем:

, ,

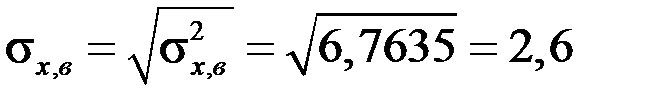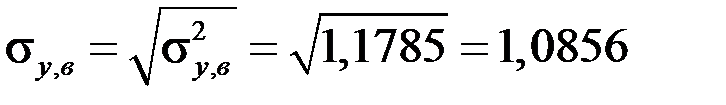выборочный корреляционный момент найдем по формуле

,

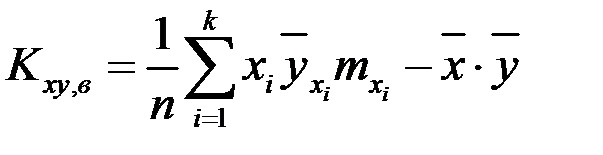в нашем случае

,

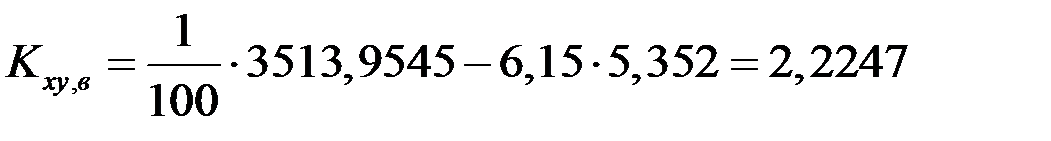выборочный коэффициент корреляции найдем по формуле

,

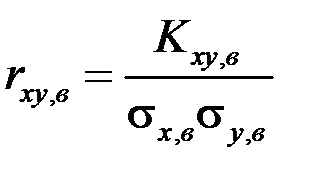в нашем случае

.

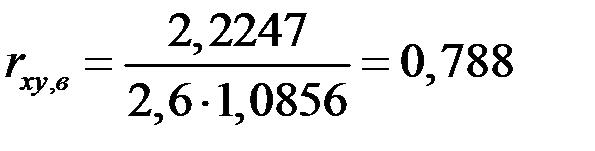Проверим гипотезу о существования связи между факторами Х и Y, вычислим :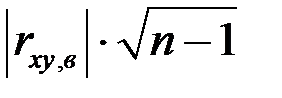

,

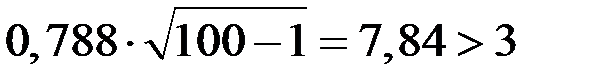следовательно, связь достаточно вероятна.

Подставим найденные значения 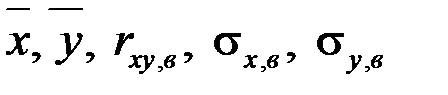в уравнение

,

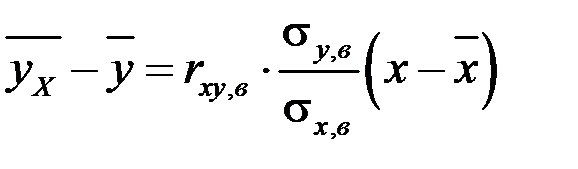получим

,

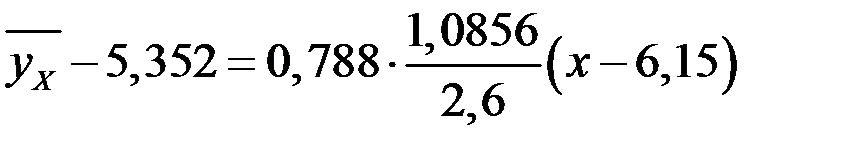после преобразований получаем уравнение эмпирической функции регрессии у на х

.

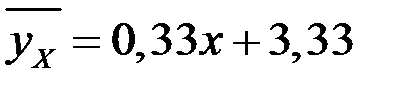3. Изобразим корреляционное поле и построим прямую 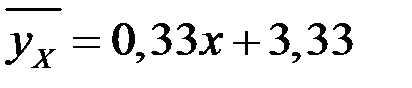(рис. 3).

Рис. 3

Краткое содержание (программа) курса

Математическая статистика

Предмет и задачи математической статистики. Генеральная и выборочная совокупности.Статистический ряд распределения. Группированный статистический ряд.Полигон частот и относительных частот. Гистограмма частот и относительных частот. Эмпирическая функция распределения, ее свойства. Числовые характеристики выборки. Понятие точечной оценки. Критерии качества точечных оценок. Метод моментов и метод наибольшего правдоподобия. Доверительные интервалы. Основные этапы решения задачи о статистической проверке гипотез. Критерий согласия 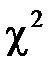(Пирсона). Выборка из двумерной генеральной совокупности, ее характеристики. Функция регрессии. Метод наименьших квадратов для нахождения неизвестных параметров функции регрессии.

Приложение 1

Значения функции Лапласа

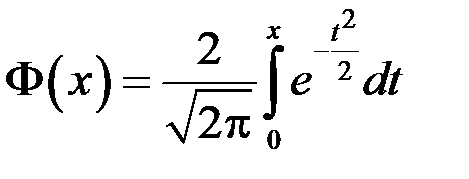
х	F(х)	х	F(х)	х	F(х)	х	F(х)
0,00	0,0000	0,30	0,2358	0,60	0,4515	0,90	0,6319
0,01	0,0080	0,31	0,2434	0,61	0,4581	0,91	0,6372
0,02	0,0160	0,32	0,2510	0,62	0,4647	0,92	0,6424
0,03	0,0239	0,33	0,2586	0,63	0,4713	0,93	0,6476
0,04	0,0319	0,34	0,2661	0,64	0,4878	0,94	0,6528
0,05	0,0399	0,35	0,2737	0,65	0,4843	0,95	0,6579
0,06	0,0478	0,36	0,2812	0,66	0,4907	0,96	0,6629
0,07	0,0558	0,37	0,2886	0,67	0,4971	0,97	0,6680
0,08	0,0638	0,38	0,2961	0,68	0,5035	0,98	0,6729
0,09	0,0717	0,39	0,3035	0,69	0,5098	0,99	0,6778
0,10	0,0797	0,40	0,3108	0,70	0,5161	1,00	0,6827
0,11	0,0876	0,41	0,3182	0,71	0,5223	1,01	0,6875
0,12	0,0955	0,42	0,3255	0,72	0,5285	1,02	0,6923
0,13	0,1034	0,43	0,3328	0,73	0,5346	1,03	0,6970
0,14	0,1113	0,44	0,3401	0,74	0,5407	1,04	0,7017
0,15	0,1192	0,45	0,3473	0,75	0,5467	1,05	0,7063
0,16	0,1271	0,46	0,3545	0,76	0,5527	1,06	0,7109
0,17	0,1350	0,47	0,3616	0,77	0,5587	1,07	0,7154
0,18	0,1428	0,48	0,3688	0,78	0,5646	1,08	0,7199
0,19	0,1507	0,49	0,3759	0,79	0,5705	1,09	0,7243
0,20	0,1585	0,50	0,3829	0,80	0,5763	1,10	0,7287
0,21	0,1663	0,51	0,3899	0,81	0,5821	1,11	0,7330
0,22	0,1741	0,52	0,3969	0,82	0,5878	1,12	0,7373
0,23	0,1819	0,53	0,4039	0,83	0,5935	1,13	0,7415
0,24	0,1897	0,54	0,4108	0,84	0,5991	1,14	0,7457
0,25	0,1974	0,55	0,4177	0,85	0,6047	1,15	0,7499
0,26	0,2051	0,56	0,4245	0,86	0,6102	1,16	0,7540
0,27	0,2128	0,57	0,4313	0,87	0,6157	1,17	0,7580
0,28	0,2205	0,58	0,4381	0,88	0,6211	1,18	0,7620
0,29	0,2282	0,59	0,4448	0,89	0,6265	1,19	0,7660
х	F(х)	х	F(х)	х	F(х)	х	F(х)
1,20	0,7699	1,50	0,8664	1,80	0,9281	2,50	0,9876
1,21	0,7737	1,51	0,8690	1,81	0,9297	2,55	0,9892
1,22	0,7775	1,52	0,8715	1,82	0,9312	2,60	0,9907
1,23	0,7813	1,53	0,8740	1,83	0,9328	2,65	0,9920
1,24	0,7850	1,54	0,8764	1,84	0,9342	2,70	0,9931
1,25	0,7887	1,55	0,8789	1,85	0,9357	2,75	0,9940
1,26	0,7923	1,56	0,8812	1,86	0,9371	2,80	0,9949
1,27	0,7959	1,57	0,8836	1,87	0,9385	2,85	0,9956
1,28	0,7995	1,58	0,8859	1,88	0,9399	2,90	0,9963
1,29	0,8029	1,59	0,8882	1,89	0,9412	2,95	0,9968
1,30	0,8064	1,60	0,8904	1,90	0,9426	3,00	0,9973
1,31	0,8098	1,61	0,8926	1,91	0,9432	3,10	0,9981
1,32	0,8132	1,62	0,8948	1,92	0,9451	3,20	0,9986
1,33	0,8165	1,63	0,8969	1,93	0,9464	3,30	0,9990
1,34	0,8198	1,64	0,8990	1,94	0,9476	3,40	0,9993
1,35	0,8230	1,65	0,9011	1,95	0,9488	3,50	0,9995
1,36	0,8262	1,66	0,9031	1,96	0,9500	3,60	0,9997
1,37	0,8293	1,67	0,9051	1,97	0,9512	3,70	0,9998
1,38	0,8324	1,68	0,9070	1,98	0,9523	3,80	0,9999
1,39	0,8355	1,69	0,9090	1,99	0,9534	3,90	0,9999
1,40	0,8385	1,70	0,9109	2,00	0,9545	4,00	0,9999
1,41	0,8415	1,71		2,05	0,9596	4,42	1-10-5
1,42	0,8444	1,72	0,9146	2,10	0,9643	4,89	1-10-6
1,43	0,8473	1,73	0,9164	2,15	0,9684	5,33	1-10-7
1,44	0,8501	1,74	0,9181	2,20	0,9722
1,45	0,8529	1,75	0,9199	2,25	0,9756
1,46	0,8557	1,76	0,9216	2,30	0,9786
1,47	0,8584	1,77	0,9233	2,35	0,9812
1,48	0,8611	1,78	0,9249	2,40	0,9836
1,49	0,8638	1,79	0,9265	2,45	0,9857

Приложение 2

Таблица значений c² в зависимости от r=n-1 и p.

	р
n-1	0,99	0,98	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05	0,02	0,01	0,001
	0,000	0,001	0,004	0,016	0,064	0,148	0,455	1,074	1,642	2,71	3,84	5,41	6,64	10,83
	0,020	0,040	0,103	0,211	0,446	0,713	1,386	2,41	3,22	4,60	5,99	7,82	9,21	13,82
	0,115	0,185	0,352	0,584	1,005	1,424	2,37	3,66	4,64	6,25	7,82	9,34	11,84	16,27
	0,297	0,429	0,711	1,064	1,649	2,20	3,36	4,88	5,99	7,78	9,49	11,67	13,28	18,46
	0,554	0,752	1,145	1,610	2,34	3,00	4,35	6,06	7,29	9,24	11,07	13,39	15,09	20,5
	0,872	1,134	1,635	2,20	3,07	3,93	5,35	7,23	8,56	10,64	12,59	15,03	16,81	22,5
	1,239	1,564	2,17	2,83	3,82	4,67	6,35	8,38	9,80	12,02	14,07	16,62	18,48	24,3
	1,646	2,03	2,73	3,49	4,59	5,53	7,34	9,52	11,03	13,36	15,51	18,17	20,1	26,1
	2,09	2,53	3,32	4,17	5,38	6,39	8,34	10,66	12,24	14,68	16,92	19,68	21,7	27,9
	2,56	3,06	3,94	4,86	6,18	7,27	9,34	11,78	13,44	15,99	18,31	21,2	23,2	29,6
	3,05	3,61	4,58	5,58	6,99	8,15	10,34	12,90	14,63	17,28	19,68	22,6	24,7	31,3
	3,57	4,18	5,23	6,30	7,81	9,03	11,34	14,01	15,81	18,55	21,0	24,1	26,2	32,9
	4,11	4,76	5,89	7,04	8,63	9,93	12,34	15,12	16,98	19,81	22,4	25,5	27,7	34,6
	4,66	5,37	6,57	7,79	9,47	10,82	13,34	16,22	18,15	21,1	23,7	26,9	29,1	36,1
	5,23	5,98	7,26	8,55	10,31	11,72	14,34	17,32	19,31	22,3	25,0	28,3	30,6	37,7
	5,81	6,61	7,96	9,31	11,15	12,62	15,34	18,42	20,5	23,5	26,3	29,6	32,0	39,3
	6,41	7,26	8,67	10,08	12,00	13,53	16,34	19,51	21,6	24,8	27,6	31,0	33,4	40,8
	7,02	7,91	9,39	10,86	12,86	14,44	17,34	20,6	22,8	26,0	28,9	32,3	34,8	42,3
	7,63	8,57	10,11	11,65	13,72	15,35	18,34	21,7	23,9	27,2	30,1	33,7	36,7	43,8
	8,26	9,24	10,85	12,44	14,58	16,27	19,34	22,8	25,0	28,4	31,4	35,0	37,6	45,3
	8,90	9,92	11,59	13,24	15,44	17,18	20,3	23,9	26,2	29,6	32,7	36,3	38,9	46,8
	9,54	10,60	12,34	14,04	16,31	18,10	21,3	24,9	27,3	30,8	33,9	37,7	40,3	48,3
	10,20	11,29	13,09	14,85	17,19	19,02	22,3	26,0	28,4	32,0	35,2	39,0	41,6	49,7
	10,86	11,99	13,85	15,66	18,06	19,94	23,3	27,1	29,6	33,2	36,4	40,3	43,0	51,2
	11,52	12,70	14,61	16,47	18,94	20,9	24,3	28,2	30,7	34,4	37,7	41,7	44,3	52,6
	12,20	13,41	15,38	17,29	19,82	21,8	25,3	29,2	31,8	35,6	38,9	42,9	45,6	54,1
	12,88	14,12	16,15	18,11	20,7	22,7	26,3	30,3	32,9	36,7	40,1	44,1	47,0	55,5
	13,56	14,85	16,93	18,94	21,6	23,6	27,3	31,4	34,0	37,9	41,3	45,4	48,3	56,9
	14,26	15,57	17,71	19,77	22,5	24,6	28,3	32,5	35,1	39,1	42,6	46,7	49,6	58,3
	14,95	16,31	18,49	20,6	23,4	25,5	29,3	33,5	36,2	40,3	43,8	48,0	50,9	59,7