Задача 5. Определение расстояния от точки до прямой.

y

M1(x1,y1)

Найти расстояние dот данной точки М₁(x₁,y₁) до данной прямой lAx+By+C=0 можно по формуле (рис. 4):

l

d

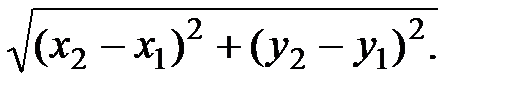d= (7)

M2(x2,y2)

x

Точка М₂(x₂,y₂) - основание перпендикуляра, опущенного из точки М₁(x₁,y₁) на прямую. Угловой коэффициент прямой М₁М₂ равен = .

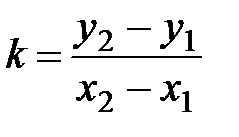Координаты точки М₂(x₂,y₂) находим из Рис. 4

решения системы уравнений

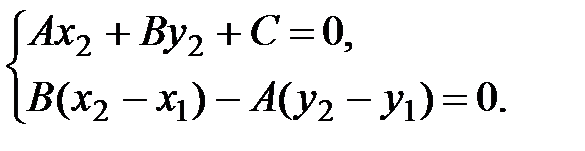(8)

Введем замену: u= x₂ -x₁;v = y₂ -y₁. Тогда (7) и (8) можно записать в виде

d= 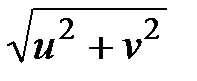; (9)

Au + Bv + Ax₁ + By₁ + C = 0;

Au-Bv= 0.

Решая систему из двух последних уравнений, находим

u= - ;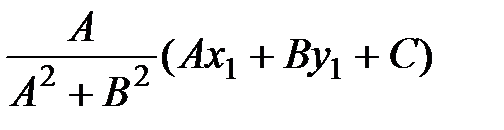

v= - .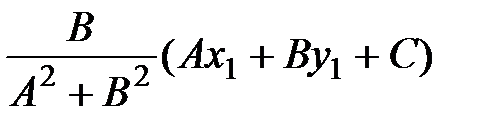

Подставив эти значения в (9), получим

d= 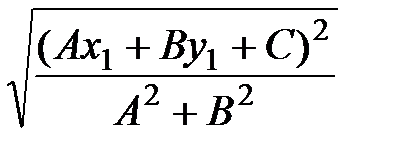= 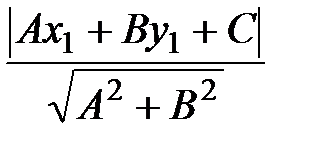. (10)

Пример 8. Найти расстояние от точки М(1,-2) до прямой 3x-2y-9 = 0.

Решение. Искомое расстояние находится по формуле (10):

d= = = . ■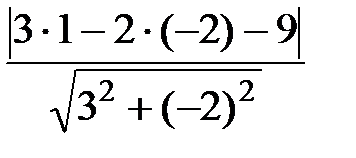

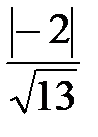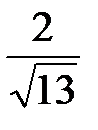2[кроме ФЭУ]. Кривые второго порядка.

Уравнение вида

Ax²+ Bxy+ Cy² + Dx + Ey + F= 0, (11)

если хотя бы одна из трех величин A, Bили Cне равна нулю, называется уравнением второго порядка, а линия, представляемая таким уравнением, -кривой второго порядка.Частными случаями линий, определяемых общим уравнением (11), являются окружность, эллипс, гипербола и парабола.

2.1 . Окружность.

Пусть дана окружность радиуса R с центром в точке М₀(x₀,y₀). Найдем ее уравнение. Для любой точки М(x,y), принадлежащей окружности, расстояние от центра до этой точки постоянно и равно радиусу окружности R, то есть ММ₀=R (для точек, не лежащих на окружности, это равенство выполняться не будет). Из формулы для определения расстояния между двумя точками следует R= 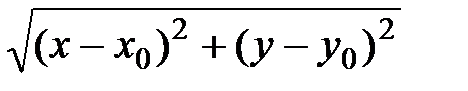(рис. 5).

Таким образом, уравнение рассматриваемой окружности имеет вид:

y

M(x,y)

R

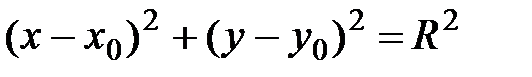. (12)

M0

Если центр окружности лежит в начале координат, то x₀= y₀= 0, а уравнение окружности приобретает видx² + y² = R².

x

Пример 9. Составить уравнение окружности радиуса 4 с центром в точке

М₀(0,-3).

Рис. 5

Решение. В данном случае x₀ = 0, y₀ = -3,

R= 4, поэтому уравнение окружности имеет вид . ■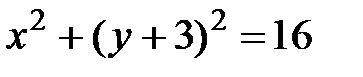

Пример 10. Выяснить геометрический смысл уравнения x²+y²+6x-2y+5=0.

Решение. Выделим в левой части уравнения полные квадраты: (x²+6x+9)+(y²-2y+1)+5-9-1=0. Отсюда 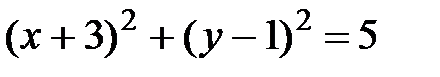. Таким образом, данное уравнение представляет собой уравнение окружности радиуса R= с центром в точке (-3,1). ■

2.2. Эллипс.

Эллипсом называется линия, для каждой точки которой сумма расстояний до двух фиксированных точек F₁ и F₂ (фокусов) есть постоянная величина, обозначаемая 2а.

Если оси декартовой системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат на расстоянии 2с друг от друга, то в этой системе координат уравнение эллипса имеет простейший вид

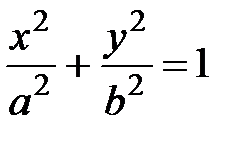. (13)

Уравнение (13) называется каноническим уравнением эллипса (оно может быть получено путем несложных алгебраических преобразований из равенстваMF₁+MF₂ = 2a). Здесь а -большая полуось, b- малая полуось эллипса; фокусы F₁ и F₂ находятся на расстоянии с = 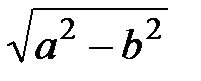от центра эллипсаО (при этом предполагается, чтоa>b). Отношение 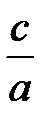=e называется эксцентриситетом эллипса (e< 1).

M(x,y)

b

-a

a

y

Если М(x,y) - произвольная точка эллипса, то отрезки MF₁ иMF₂ (рис. 6) называются фокальными радиусами точкиM и определяются по формулам

x

F2

F1 0

MF₁ = a+e x, MF₂ = a-e x. (14)

-b

Замечание.Еслиa = b, то уравнение (13) определяет окружность, рассматриваемую как

частный случай эллипса. При этом Рис. 6

эксцентриситет окружности e= 0.

Пример 11. Составить уравнение эллипса, симметричного относительно осей координат и проходящего через точки М₁(4,- 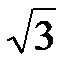) и М₂(2 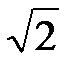,3), а также найти расстояние между фокусами и эксцентриситет эллипса.

Решение. Подставляя координаты точек М₁ и М₂ в уравнение (13), получаем систему двух уравнений:

, .

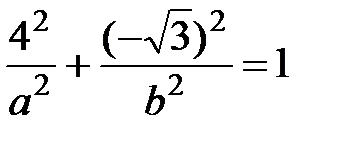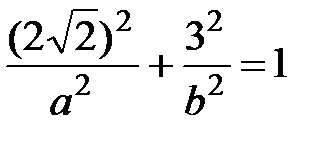Решая эту систему находим полуосиa= 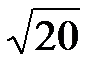и b= 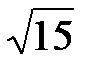. Искомое уравнение эллипса 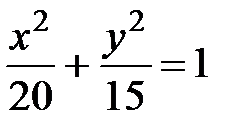. Находим, далее, с = 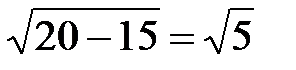и расстояние между фокусами 2с =2 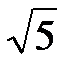. Эксцентриситет эллипса e= 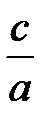= = 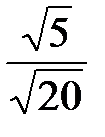=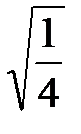0,5. ■

Пример 12. Убедившись, что точка М(-4; 2,4) лежит на эллипсе 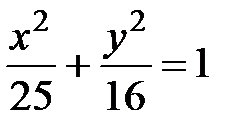, определить фокальные радиусы точки М.

Решение. Подставляя координаты точки М в уравнение эллипса 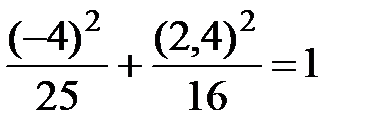, получаем верное равенство, доказывающее, что М- точка эллипса. Фокальные радиусы точки М находим по формулам (14), полагая a=5, b=4, с = 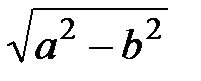= =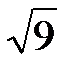3, e= = :

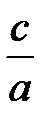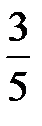MF₁ = a+ex = 5+ 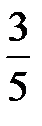×(-4) = 2,6; MF₂ = a-ex = 5- 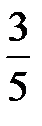×(-4) = 7,4. ■

2.3. Гипербола.

Гиперболой называется линия, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек F₁ и F₂ (фокусов) есть постоянная величина, обозначаемая 2а.

В системе координат, изображенной на рис. 7, уравнение гиперболы имеет простейший вид

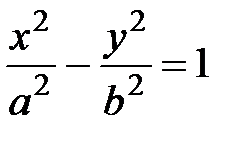, (15)

называемыйканоническим уравнением гиперболы.

F2 y

F1 y

-a

a y

-b y

b y

y

x

M(x,y)

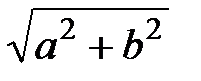Уравнение (15) получено из равенства |MF₁-MF₂ | = 2a. Здесь а называется действительной полуосью, b- мнимой полуосью гиперболы; фокусыF₁ и F₂ находятся на расстоянии с = от центра гиперболыО (при этом а может быть как больше, так и меньше b). Отношение 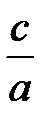= e называется эксцентриситетом гиперболы (e> 1).

Прямые y = 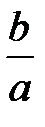x иy = - 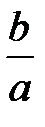x называются асимптотами гиперболы; при неограниченном продвижении точки М(x,y) вдоль гиперболы в бесконечность расстояние от М до соответствующей асимптоты стремится к нулю.

Расстояния от любой точки М(x,y) гиперболы до ее фокусовF₁ и F₂-фокальные радиусы точки М- определяются по формулам:

MF₁ = |ex+a|, MF₂= |ex-a|. (16)

Две гиперболы, заданные уравнениями

,

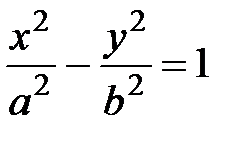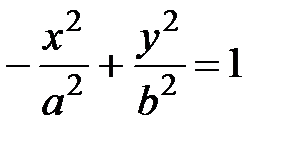
в одной и той же системе координат, называются сопряженными.

Пример 13. Составить каноническое уравнение гиперболы, проходящей через точки М₁(6,-1) и М₂(-8,2 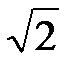), и найти ее асимптоты.

Решение. Подставляя координаты точек М₁ и М₂ в уравнение (15), получаем систему двух уравнений относительно неизвестных полуосей гиперболы a и b:

, .

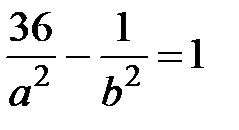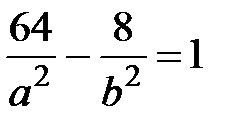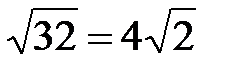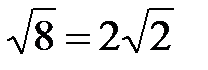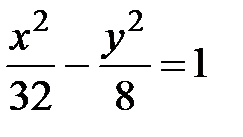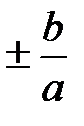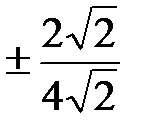Из этой системы находим а² = 32, b² =8. Таким образом, действительная полуось гиперболы a= , а мнимая полуось b= . Искомое уравнение гиперболы . Асимптоты определяются по формуле y = x = x = . ■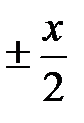

Пример 14. Найти координаты фокусов гиперболы 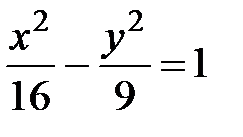, а также расстояния от точки М(-5, ) до фокусов гиперболы.

Решение. Имеем с = 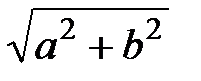= 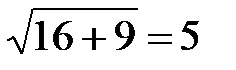, так что расстояние между фокусами равно 2с = 10, а координаты фокусовF₁(-5,0) и F₂(5,0).

Точка М(-5, ) принадлежит гиперболе (в чём легко убедиться подстановкой её координат в уравнение гиперболы), поэтому искомые расстояния до фокусов вычисляем по формулам (16), полагая в них a = 4, эксцентриситет e= 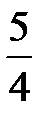: MF₁ =| 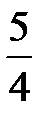×(-5) + 4| = 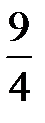; MF₂ =| 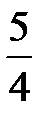×(-5) - 4| = . ■

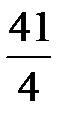Замечание. Если в уравнении (15)a = b, то гиперболу в этом случае называют равнобочной; ее уравнение имеет вид x² -y² = а²; асимптоты y = x иy = -x взаимно перпендикулярны; эксцентриситет равен 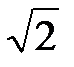. Если взять асимптоты равнобочной гиперболы в качестве новых осей координат, то в такой системе координат 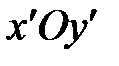гипербола представляет собой график обратной пропорциональной зависимости с уравнением 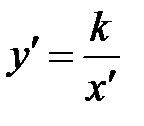, где k= .

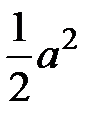2.4. Парабола.

Параболой называется линия, для каждой точки которой расстояние до фиксированной точки F (фокуса) равно расстоянию до данной прямой, называемой директрисой.

Расстояние FС = рот фокуса до директрисы называется параметром параболы.

Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно директрисе и была направлена от директрисы к фокусу; начало координатОрасположим посередине между фокусом и директрисой, так что FО=ОС= 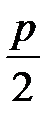(рис. 8).

y

y

K

M(x,y)

-p/2

x

F y

x

-p/2

а)Рис. 8б)

В этой системе координат парабола будет определяться уравнением

y² = 2px.(17)

Уравнение (17) называется каноническим уравнением параболы (оно получается из равенстваFМ=МК). В этой же системе координат фокус данной параболыF( 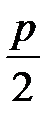,0), а директриса имеет уравнениеx= 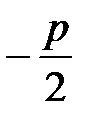. Фокальный радиус произвольной точки М(x,y) параболы (то есть длина отрезка FМ) может быть вычислен по формуле MF=x+ .

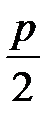Уравнение x² = 2py или же y = аx² (где а= 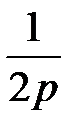), так же как и уравнение (17) представляет параболу, только в этом случае ось параболы совпадает с осью ординат и парабола расположена так, как показано на рис. 8(б). Её фокус F(0, 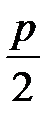), а директриса имеет уравнение y= 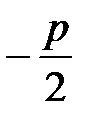. Если в уравнении y=аx² коэффициента отрицателен, то ветви параболы направлены вниз.

Пример 15. Составить уравнение параболы, проходящей через начало координат, точку М(1,-2) и симметричной относительно оси абсцисс; написать уравнение директрисы; найти фокальный радиус точки М.

Решение. Подставив координаты точки М (x= 1, y= -2) в уравнение y² = 2px, получим 4=2p×1, р=2, так что уравнение параболы y² = 4x. Уравнение директрисы x = -1. Фокальный радиус MF=1+ 1 =2. ■