Цели и задачи практической работы

1) Решить задачу Коши (1)-(2) (или (3)-(4)) наиболее известными и широко используемыми на практике методами Рунге-Кутта второго и четвертого порядка точности, аппроксимировав дифференциальную задачу соответствующей разностной схемой (на равномерной сетке); полученное конечно-разностное уравнение (или уравнения в случае системы), представляющее фактически некоторую рекуррентную формулу, просчитать численно;

2) Найти численное решение задачи и построить его график;

3) Найденное численное решение сравнить с точным решением дифференциального уравнения (подобрать специальные тесты, где аналитические решения находятся в классе элементарных функций, при проверке можно использовать ресурсы on-line системы http://www.wolframalpha.com или пакета Maple и т.п.).

Отчет по практической работе

Отчет должен содержать

§ титульный лист (образец прилагается);

§ описание постановки задачи и ее целей;

§ описание метода (алгоритма) решения;

§ описание программы и ее оригинальный текст с комментариями;

§ тесты, доказывающие корректность работы программы (не менее 3-5 тестов, проверенных непосредственно вручную или с помощью специализированного программного обеспечения.

Варианты заданий

Таблица 1.

Варианты задания правой части уравнения (1) и начального условия (2)

в случае одного дифференциального уравнения

Вариант		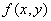	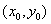Точное решение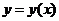

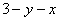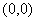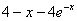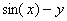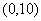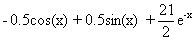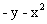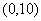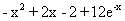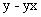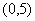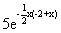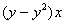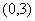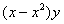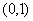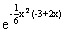Таблица 2.

Варианты задания правых частей системы (3) и начального условия (4)

в случае системы двух обыкновенных дифференциальных уравнений

Вариант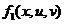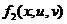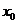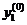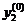
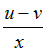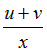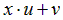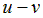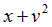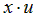					-1
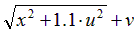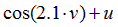				0.5
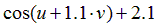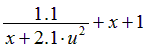					0.05
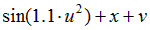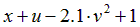					0.5
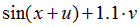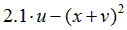				0.5
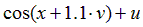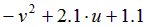				0.25
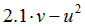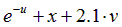					0.25
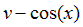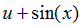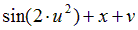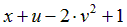					0.5
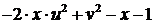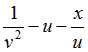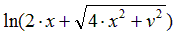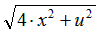				0.5
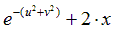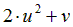				0.5
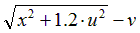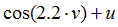				0.5
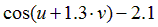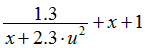					0.05
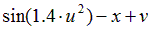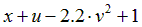					0.5
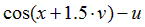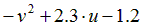				0.25
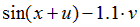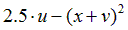				0.5
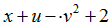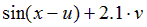				1.5
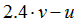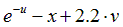					0.25

ПРАКТИЧЕСКАЯ РАБОТА № 2 (2)

Подвариант № 2

РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, РАЗРЕШЕННОГО ОТНОСИТЕЛЬНО СТАРШЕЙ ПРОИЗВОДНОЙ

Цель работы

освоить метод прогонки решения краевой задачи для дифференциального уравнения второго порядка.

Постановка задачи

Рассматривается линейное дифференциальное уравнение второго порядка вида

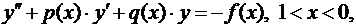(1)

с дополнительными условиями в граничных точках

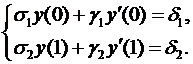(2)

Цели и задачи практической работы

1) Решить краевую задачу (1)-(2) методом конечных разностей, аппроксимировав ее разностной схемой второго порядка точности (на равномерной сетке); полученную систему конечно-разностных уравнений решить методом прогонки;

2) Найти разностное решение задачи и построить его график;

3) Найденное разностное решение сравнить с точным решением дифференциального уравнения (подобрать специальные тесты, где аналитические решения находятся в классе элементарных функций, при проверке можно использовать ресурсы on-line системы http://www.wolframalpha.com или пакета Maple и т.п.).