Непрерывная модель электродвигателя постоянного тока независимого возбуждения

В данном параграфе на примере двигателя постоянного тока независимого возбуждения (ДПТ НВ) рассмотрим создание S-функции для модели реального объекта.

Математическое описание ДПТ НВ

Двигатель постоянного тока независимого возбуждения (рис. 16.9), описывается следующей системой дифференциальных и алгебраических уравнений в абсолютных единицах:

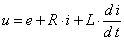	(1)
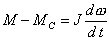	(2)
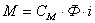	(3)
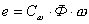	(4)

где

u - напряжение на якорной обмотке двигателя,e - электродвижущая сила (ЭДС) якоря,i - ток якоря,Ф - поток, создаваемый обмоткой возбуждения,M - электромагнитный момент двигателя,M_С - момент сопротивления движению, - скорость вращения вала двигателя,R - активное сопротивление якорной цепи,L - индуктивность якорной цепи,J - суммарный момент инерции якоря и нагрузки,С - коэффициент связи между скоростью и ЭДС,С_М - коэффициент связи между током якоря и электромагнитным моментом.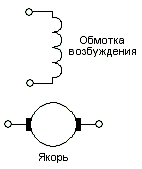

Рис. 16.9 Двигатель постоянного тока с независимым возбуждением.

С точки зрения будущей модели, входными воздействиями являются напряжения якоря u и момент сопротивления движению M_С , выходными переменными - электромагнитный момент двигателя M и скорость вращения вала двигателя , а переменными состояния - переменные стоящие под знаком производной: ток якоря i и скорость вращения вала двигателя . Остальные переменные, входящие в состав уравнений (1) - (4) являются параметрами, численные значения которых, необходимо будет задавать при проведении расчетов.

Преобразуем дифференциальные уравнения (1) и (2) к явной форме Коши и выполним подстановку. Система уравнений примет вид:

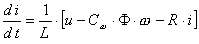	(5)
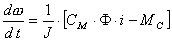	(6)
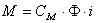	(7)
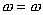	(8)

Последнее уравнение есть отражение того факта, что переменная состояния является также и выходной переменной.

Введем "машинные" переменные. Входные переменные: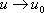 , . . 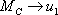Выходные переменные: 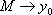, . , 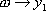Переменные состояния: , .

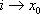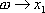Тогда уравнения (5) - (8) примут вид:

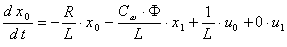	(9)
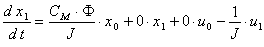	(10)
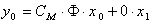	(11)
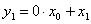	(12)

Перепишем систему уравнений в матричной форме:

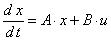	(13)
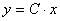	(14)

где

,

,

.

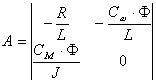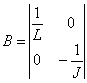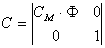Отметим, что в получившейся системе уравнений входные переменные не участвуют в формировании выходных переменных (матрица обхода D - отсутствует) и, следовательно, параметр sizes.DirFeedthrough, определяемый при инициализации S-функции должен быть задан равным нулю.

Пример S-функции для ДПТ НВ

Для создания S-функции для ДПТ НВ за основу взят файл примера модели непрерывной системы csfunc.m . Принципиальные отличия нового файла от образца сводятся к следующему:

1. Для расчета матриц уравнений пространства состояния A, В и С используются параметры передаваемые в S-функцию через окно диалога блока S-function. Эти параметры (L,R,J,Cm,Cw,Fi) записываются в конце списка параметров в заголовке S-функции : function [sys,x0,str,ts] = dpt_sfunc_1(t,x,u,flag,L,R,J,Cm,Cw,Fi)

2. Для исключения одинаковых (повторяющихся) вычислений расчет матриц A, В и С выполняется в методе mdlInitializeSizes. Для этого параметры блока (L,R,J,Cm,Cw,Fi) передаются в метод mdlInitializeSizes через его заголовок: [sys,x0,str,ts] = mdlInitializeSizes(L,R,J,Cm,Cw,Fi) Поскольку инициализация модели происходит лишь один раз, то и расчет матриц A, В и С будет выполнен также один раз, что значительно повысит скорость моделирования.

3. Передача рассчитанных в mdlInitializeSizes матриц выполняется с помощью глобальных переменных. Для этого объявления вида: global A B C; выполнены в теле S-функции, методе mdlInitializeSizes (где выполняется расчет этих матриц), а также методах mdlDerivatives и mdlOutputs (где эти матрицы используются для расчетов).

4. Поскольку в уравнения пространства-состояния матрица D отсутствует (входные переменные не участвуют в формировании выходных переменных), то параметр sizes.DirFeedthrough в методе mdlInitializeSizes задан равным нулю.

Ниже приводится текст S-функции dpt_sfunc_1 (файл dpt_sfunc_1.m):

function [sys,x0,str,ts] = dpt_sfunc_1(t,x,u,flag,L,R,J,Cm,Cw,Fi)% DPT_SFUNC_1 Пример S-функции для моделирования двигателя постоянного тока% независимого возбуждения.%% В примере выполняется моделирование с помощью уравнений% пространства-состояния:% x' = Ax + Bu% y = Cx + Du%% Copyright 2002, Chernykh ILya% $Revision: 1.8% Автор: Черных И.В.%% Параметры S-функции, передаваемые через окно диалога блока S-function:%% L - Индуктивность цепи якоря % R - Активное сопротивление цепи якоря % J - Момент инерции% Cm - Коэффициент связи между моментом и током% Cw - Коэффициент связи между потоком и скоростью вращения вала% Fi - Поток, создаваемый обмоткой возбуждения%global A B C; % Объявление глобальными переменных, необходимых для % расчетов внутри функций mdlDerivatives и mdlOutputs . % Сами матрицы расчитываются в методе mdlInitializeSizes . switch flag, % В зависимости от значения переменной flag происходит % вызов того или иного метода: %===============%% Инициализация %%===============% case 0, [sys,x0,str,ts]=mdlInitializeSizes(L,R,J,Cm,Cw,Fi); %====================%% Расчет производных %%====================% case 1, sys=mdlDerivatives(t,x,u); %===========================================%% Расчет значений вектора выходных сигналов %%===========================================% case 3, sys=mdlOutputs(t,x,u); %=========================================%% Неиcпользуемые значения переменной flag %%=========================================% case { 2, 4, 9 }, sys = []; %======================================%% Неизвестное значение переменной flag %%======================================% otherwise error(['Unhandled flag = ',num2str(flag)]); end% Окончание dpt_sfunc_1 %===============================================================%% mdlInitializeSizes %% Функция инициализации %% Расчет начальных условий, значений вектора шагов модельного %% времени,размерности матриц %%===============================================================% function [sys,x0,str,ts]=mdlInitializeSizes(L,R,J,Cm,Cw,Fi) sizes = simsizes; sizes.NumContStates = 2; % Число непрерывных переменных состояния % В данном случае этот параметр равен 2 % (ток якоря и скорость вращения вала). sizes.NumDiscStates = 0; % Число дискретных переменных состояния % В данном случае этот параметр равен 0, % поскольку модель непрерывная. sizes.NumOutputs = 2; % Число выходных переменных (размерность выходного % вектора). В данном случае этот параметр равен 2 % (скорость вращения и момент на валу). sizes.NumInputs = 2; % Число входных переменных (размерность входного % вектора). В данном случае этот параметр равен 2 % (напряжение на обмотке якоря и момент % сопротивления). sizes.DirFeedthrough = 0; % Прямой проход. Значение параметра равно нулю, % поскольку матрица обхода D - отсутствует (входные % переменные не участвуют в формировании выходных % переменных). sizes.NumSampleTimes = 1; % Размерность вектора модельного времени. sys = simsizes(sizes); x0 = zeros(2,1); % Задание вектора начальных значений переменных % состояния. Начальные условия нулевые. str = []; % Зарезервированный параметр ts = [0 0]; % Матрица из двух колонок, задающая шаг модельного % времени и смещение. % Далее в функцию mdlInitializeSizes добавлены операторы для% вычисления матриц A, B и C уравнений пространства состояния% модели двигателя постоянного тока global A B C; % Объявление глобальными переменных, необходимых для % расчетов внутри функций mdlDerivatives и mdlOutputs. % Расчет матриц А,В и С:%A=[-R/L -Cw*Fi/L Cm*Fi/J 0 ];%B=[1/L 0 0 -1/J];%C=[Cm*Fi 0 0 1];% Окончание mdlInitializeSizes %========================================================================%%mdlDerivatives %% Функция для расчета значений производных вектора состояния непрерывной %% части системы %%========================================================================% function sys=mdlDerivatives(t,x,u)%global A B; % Объявление глобальными переменных, необходимых для % расчетов внутри метода.sys = A*x + B*u; % Окончание mdlDerivatives %========================================================% % mdlOutputs %% Функция для расчета значений вектора выходных сигналов %%========================================================% function sys=mdlOutputs(t,x,u) global C; % Объявление глобальными переменных, необходимых для % расчетов внутри метода.sys = C*x; % Окончание mdlOutputs

На рис.16.10 показаны модели двигателя постоянного тока на базе S-функции и с использованием стандартных блоков. Результаты расчета для обеих моделей идентичны. Окно диалога блока S-function изображено на рис. 16.11.

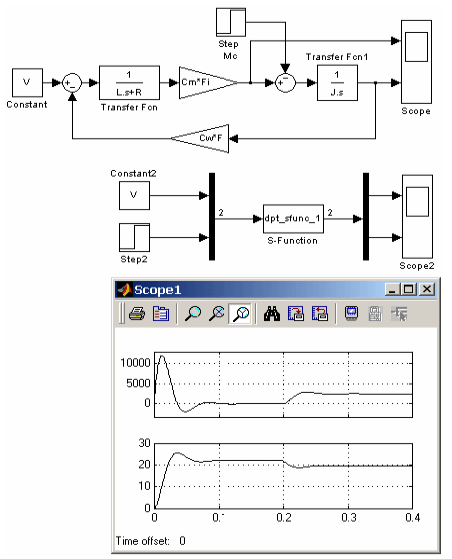Рис. 16.10 Модели ДПТ НВ

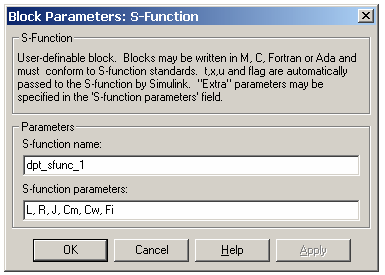Рис. 16.11 Окно диалога блока S-function

[Скачать пример]