Математическая логика и теория алгоритмов.

2.1. ЛОГИЧЕСКИЕ ОПЕРАЦИИ. ТАБЛИЦЫ ИСТИННОСТИ.

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание).

Высказывания А и В равносильны тогда и только тогда, когда истинностные значения А и В совпадают ( ).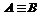

Таблица истинности – таблица, описывающая логическую операцию (или функцию), в ней перечислены все значения логической операции для всех возможных значений аргументов.

Логические операции над высказываниями.

1. Отрицание. 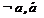. Не а. Унарная операция.

a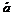

2. Конъюнкция. 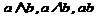. a И b.

a	b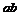

3. Дизъюнкция. 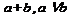. a ИЛИ b.

a	b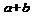

4. Импликация. 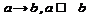. ЕСЛИ a, ТО b. a – посылка, b – заключение.

a	b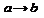

5. Эквиваленция. 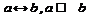. ТОГДА И ТОЛЬКО ТОГДА

a	b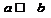

Если х делится на 4, то x делится на 2.

А: х делится на 4.

B: х делится на 2.

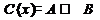
Формулы.

1. Снятие импликации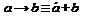

2. Снятие эквиваленции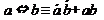

3. Переместительный (коммуникативный) закон ,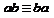

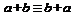
4. Сочетательный (ассоциативный) закон ,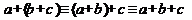

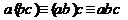
5. Распределительный (дистрибутивный) закон , .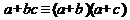

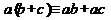6. Законы Де Моргана ,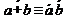

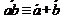
7. Законы поглощения , .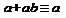

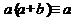8. Законы идемпотентности , .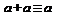

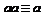9. Законы нуля и единицы , , ,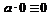

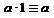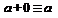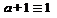
10. Закон исключающего третьего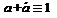

11. Закон противоречия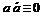

12.Закон двойного отрицания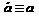

2.2. ЛОГИКА ВЫСКАЗЫВАНИ И ПРЕДИКАТОВ.

Логическое высказывание – связанное повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание). В логике высказываний нас интересует не содержание, а истинностное значение высказываний (0 – Ложь, 1 – Истина).

Высказывания А и В равносильны тогда и только тогда, когда истинностные значения А и В совпадают ( ).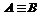

Основные операции над логическими высказываниями: (см. вопрос 2.1).

Логика предикатов – логическая система, средствами которой можно исследовать структуру высказываний.

Предикат – свойство объекта (отношения между объектами). Быть чётным, быть простым, делиться, быть больше.

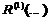– унарный.

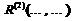– бинарный.

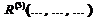– трёхместный.

Предикат – функция, высказывательные переменные которой принимают значения из некоторого множества 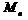, а сама функция принимает значения {0; 1}.

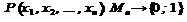
Для задания предиката должно быть задано:

1. Область определения 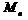, состоящая из множества предметных переменных.

2. Множество 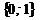– область значений предиката.

3. Правило, по которому каждому элементу из множества 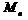ставится в соответствие элемент из множества .

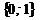Способы задания предиката.

1. Графический.

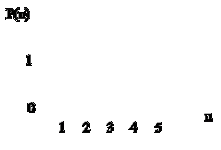
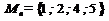
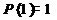
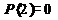
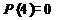
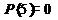
2. Табличный

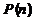3. Словесный

Предикат 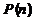выполняется при 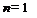и не выполняется во всех остальных точках x области определения.

4. Формульный (аналитический).

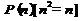
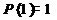
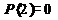
В логике предикатов для образования предложений можно использовать те же логические операции, что и в логике высказываний, т.е. дизъюнкцию, конъюнкцию, эквиваленцию, в результате получаются новые предикаты.

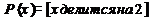
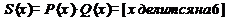
Кванторы.

1. Квантор общности. 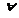. Пусть 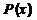– некоторый предикат, под выражением 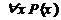будем подразумевать высказывание, истинное когда 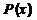истина для любого 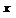из множества 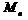и ложное в противоположном случае.

2. Квантор существования. 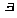. Пусть 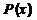– некоторый предикат, под выражением 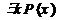будем подразумевать высказывание, истинное когда существует элемент из множества 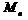, для которого 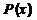истинно и ложное в противоположном случае. 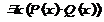. Существует такое x, которое кратно 2 и кратно 3.

Операции, уменьшающие местность предиката.

1. Фиксация значений переменной.

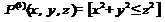
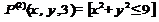
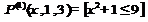
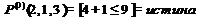
2. Операция связывания квантором

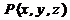
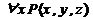
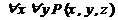
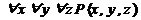
Обобщение логических операций с помощью квантора.

Пусть 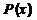– одноместный предикат, который определён на конечном множестве 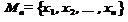. . 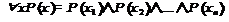Квантор общности определяет операцию конъюнкция.

Квантор существования обобщает операцию дизъюнкция.

Основные равносильности алгебры предикатов, содержащие кванторы.

1. Законы де Моргана. 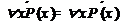, 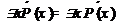(перенос отрицания).

2. Перестановка одноимённых кванторов (коммунитативные законы). , .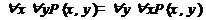

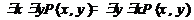3. Дистрибутивные законы. ,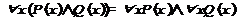

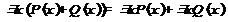
4. Законы ограничения действия кванторов , , , .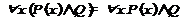

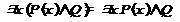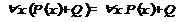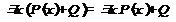Все законы, которые работают в алгебре высказываний, переносятся в алгебру предикатов.

2.3. ИНТУИТИВНОЕ И ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ АЛГОРИТМА.

Алгоритм – эффективная процедура, однозначно приводящая к результату.

Основные требования к алгоритму:

· Каждый алгоритм должен иметь данные: входные, выходные, промежуточные

· Данные для своего размещения требуют памяти внутренней и внешней

· Алгоритм состоит из отдельных элементарных шагов, количество которых конечно

· Последовательность шагов алгоритма детерминирована, т.е. после каждого шага либо указывается какой шаг делать дальше либо дается команда остановки

· Результативность – остановка после конечного числа шагов, с указанием того, что считать результатом

Алгоритмическая модель – формализация понятия алгоритма, она является универсальной, т.е. допускается описание любых алгоритмов.

Основные типы алгоритмических моделей:

1. Рекурсивные функции – вычисление и числовые функции

2. Машина Тьюринга – в основе лежит представление об алгоритме как некотором детерминированном устройстве, способном выполнить в каждый отдельный момент времени лишь примитивные операции

3. Каноническая система Поста и нормальные алгоритмы Маркова – происходит преобразование слов в произвольных алфавитах, в которых элементарные операции – это подстановки, т.е. замены части слова другим словом.

Пример: Машина Тьюринга

Машина Тьюринга состоит из 3-х частей:

1) Устройство управления, которое может находиться в одном из следующих состояний: Q = {q₁, q₂, …, q_n}.

2) Лента, которая разбита на ячейки, в каждой из которых может быть записан один из символов конечного алфавита A = {a₁, a₂, …, a_n}.

3) Устройство обращения к ленте, которая представляет из себя считывающую и пишущую головку. В каждый момент времени она обозревает ячейку ленты и в зависимости от символа на ленте и состоянию устройств управления, записывает в ячейку символ, который может быть пустым, т.е. стирает содержимое, сдвигается на ячейку влево или вправо, или остается на месте. После этого устройство управления переходит в новое состояние или остается в старом.

Среди состояний устройства управлений выделяют начальное – q₁ (оно существует перед началом работы) и выделяется заключительное состояние – q_z, после этого состояния машина Тьюринга останавливается.

Три способа описания:

1. Система команд

2. Таблица переходов: строки таблицы – состояния, столбцы – входные символы

3.Блок – схемы (диаграмма переходов)

2.4. ТЕОРИЯ СЛОЖНОСТИ В ТЕОРИИ АЛГОРИТМОВ.

В информатике, теория сложности вычислений является разделом теории вычислений, изучающим стоимость работы. Стоимость обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения проблемы, тогда как пространство определяется объёмом памяти или места на носителе данных.

Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.

Временная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения задачи. Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае.

Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное её значение бессмысленно. Дело в том, что точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций или операций на машине Тьюринга).

По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объёме используемой памяти.

Классы сложности.

Классами сложности – множества вычислительных задач, примерно одинаковых по сложности вычисления.

1. Класс P (от англ. polynomial) – класс алгоритмов, работающих за полиноминальное время, время работы не существенно зависит от размера входных данных. Стандартные алгоритмы целочисленного сложения, перемножения матриц и др.

2. Класс NP (от англ. non-deterministic polynomial) – класс алгоритмов, время работы которых существенно зависит от размера входных данных; в то же время, если предоставить алгоритму некоторые дополнительные сведения (сертификат решения), то он сможет достаточно быстро решить задачу. Задача выполнимости булевых формул: узнать по данной булевой формуле, существует ли набор входящих в неё переменных, обращающий её в 1. Сертификат — такой набор. Существование целочисленного решения у заданной системы линейных неравенств. Сертификат — решение.

3.Класс BPP (от англ. bounded-error, probabilistic, polynomial) – класс алгоритмов, быстро (за полиномиальное время) вычислимых и дающих ответ с высокой вероятностью (причём, жертвуя временем, можно добиться сколь угодно высокой точности ответа). Решение СЛАУ методом половинного деления, методом хорд и др.

ОРГАНИЗАЦИЯ ЭВМ И СИСТЕМ.

3.1. Принцип программного управления

Такое определение подчеркивает, что в основу ЭВМ положен принцип программного управления. Один из способов его реализации был предложен в 1945 г. американским математиком Дж. фон Нейманом, и с тех пор неймановский принцип программного управления используется в качестве основного принципа построения ЭВМ. Этот принцип состоит в следующем:

• информация кодируется в двоичной форме и разделяется на единицы (элементы) информации — слова;
• разнотипные слова информации различаются по способу использования, но не способами кодирования;
• слова информации размещаются в ячейках памяти машины и идентифицируются номерами ячеек, которые называются адресами слов;
• алгоритм представляется в форме последовательности управляющих слов — команд, которые определяют наименование операции и слова информации, участвующие в операции. Алгоритм, представленный в терминах машинных команд, называется программой;
• выполнение вычислений, предписанных алгоритмом, сводится к последовательному выполнению команд в порядке, однозначно определяемом программой. Первой выполняется команда, заданная пусковым адресом программы. Обычно это адрес первой команды программы. Адрес следующей команды однозначно определяется в процессе выполнения текущей команды и может быть либо адресом следующей по порядку команды, либо адресом любой другой команды. Процесс вычислений продолжается до тех пор, пока не будет выполнена команда, предписывающая прекращение вычислений.

Выборка программы из памяти осуществляется с помощью счетчика команд. Процессор начинает работу после того, как программа записана в память ЭВМ, а в счетчик команд записан адрес первой команды программы. Счётчик команд процессора последовательно увеличивает хранимый в нем адрес очередной команды на длину команды.

Работу процессора можно описать следующим циклом: чтение команды из памяти по адресу, записанному в СК, увеличение СК на длину прочитанной команды , выполнение прочитанной команды.

А так как команды программы расположены в памяти друг за другом, то тем самым организуется выборка цепочки команд из последовательно расположенных ячеек памяти. Если же нужно после выполнения команды перейти не к следующей, а к какой-то другой, используются командыусловного илибезусловного перехода, которые заносят в счетчик команд номер ячейки памяти, содержащей следующую команду. Выборка команд из памяти прекращается после достижения и выполнения команды «стоп».

Таким образом,процессор исполняет программу автоматически, команду за командой,без вмешательства человека.

3.2. Структуры ЭВМ и вычислительных систем.

Вычислительный процесс должен быть предварительно представлен для ЭВМ в виде программы — последовательности инструкций (команд), записанных в порядке выполнения. В процессе выполнения программы ЭВМ выбирает очередную команду, расшифровывает ее, определяет, какие действия и над какими операндами следует выполнить. Эту функцию осуществляет УУ. Оно же помещает выбранные из ЗУ операнды в АЛУ, где они и обрабатываются. Само АЛУ работает под управлением УУ.

Обрабатываемые данные и выполняемая программа должны находиться в запоминающем устройстве — памяти ЭВМ, куда они вводятся через устройство ввода. Данные, которые хранятся на внешних носителях, доступны программе через устройства ввода\вывода.

Достоинства и недостатки архитектуры вычислительных машин и систем изначально зависят от способа соединения компонентов. При самом общем подходе можно говорить о двух основных типах структур вычислительных машин и двух типах структур вычислительных систем.