Оптимизация геометрических параметров балок

Сечение коробчатой или двутавровой балки имеет как минимум четыре параметра: 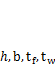(рис. 13.1, б, д, считаем, что ),а несимметричные сечения — еще больше. Поскольку уравнений, которые можно использо­вать для их определения, всегда меньше, то существует множество комбинаций значений этих параметров, кото­рые удовлетворяют условиям работоспособности. Следо­вательно, можно найти комбинацию параметров, наилуч­шую по некоему дополнительному критерию, выполнение которого не обязательно, но желательно. Зависимость это­го дополнительного критерия от параметров конструкции называется целевой функцией. Математический процесс отыскания такого решения, которое дает экстремальное значение целевой функции, называется оптимизацией. При оптимизации параметров сечения балки целевой функци­ей может являться зависимость массы балки от ее высо­ты. Значение высоты, соответствующее минимальной мас­се, называется оптимальным. При этом следует понимать, что решение, оптимальное по массе, не обязательно будет оптимальным по себестоимости, так как существенное зна­чение имеет и трудоемкость изготовления.

Погонная масса балки выражается формулой 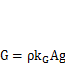(п. 6.3). Приняв допущение о том, что конструктивный ко­эффициент не зависит от габаритных размеров сечения, условие минимальной массы можем заменить усло­вием минимальной площади сечения. Рассмотрим два ва­рианта оптимизации сечения коробчатой балки, исполь­зуя: в первом случае условия прочности и минимальной массы, во втором — условия жесткости и минимальной массы. Будем считать, что балка загружается изгибом толь­ко в одной плоскости или изгибающий момент в другой плоскости настолько мал, что в предварительных расче­тах им можно пренебречь.

1. Балка должна удовлетворять условию прочности

(13.20)

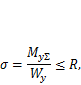
где — максимальный изгибающий момент в балке от эксплуатационных нагрузок выбранной комбинации II рас­четного случая (п. 6.1); _y— момент сопротивления сече­ния балки; R— предельное напряжение по условию проч­ности: в СРДН R= [ ], в СРПС 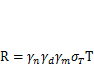(п- 1-5.2).

Условие минимальной площади сечения имеет вид dA/dh= 0. Поставим задачу определить значение высоты балки h_os,обеспечивающее минимальную площадь сечения.

Из уравнений (13.20) найдем минимально необходимое значение момента сопротивления 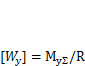.Приняв 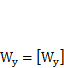и подставив сюда формулу для момента сопро­тивления сечения балки из (13.8), найдем площадь пояса: 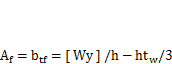.Подставим ее в выражение для пло­щади сечения балки:

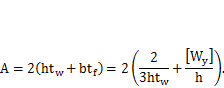
Из условия 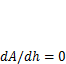найдем оптимальную высоту балки

(13.21)

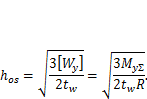
Таким образом, задав толщину стенки из конструктивных или технологических соображений, по формуле (13.21) можем найти оптимальную высоту коробчатой балки. В аналогичном выражении для балки двутаврового се­чения с двумя осями симметрии в знаменателе отсутствует множитель 2. Отступления от оптимальной высоты в пределах -25...+40 % приводят к увеличению площади расчетного сечения не более чем на 5 %. Оптимальная высота балки при необходимости может быть скорректи­рована по условию жесткости или из конструктивных со­ображений, по условиям компоновки механизмов либо ра­бочих органов.

2. В ряде случаев определяющим критерием при проек­тировании балки является не условие прочности, а усло­вие жесткости (8.1). В таких случаях полезно иметь мето­дику оценки оптимальной высоты балки с учетом этого критерия.

В общем виде выражение для вычисления прогиба балки (8.2) можно записать как 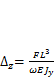Используяусловие жесткости (8.1) со знаком равенства, можем найти минимально необходимый момент инерции балки:

(13.22)

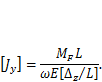
Здесь — максимальный изгибающий момент в балке от переменной нагрузки (например, веса тележки с грузом в мостовых кранах). Для схем, представленных на рис. 8.1, согласно (8.2) значения момента и коэффициента вычисляются по формулам:

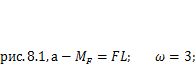
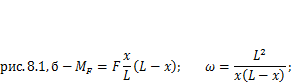
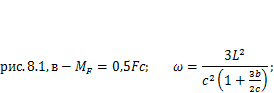
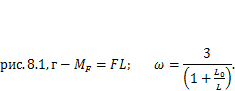
Подставив в равенство 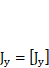выражение для (13.7),найдем площадь сечения пояса

(13.23)

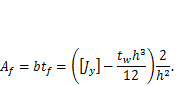
Подставив (13.22) и (13.23) в выражение для площади сечения 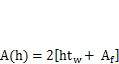, как и в предыдущем случае, продифференцируем его и из условия dA/dh= 0 найдем оптимальную высоту балки

(13.24)

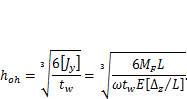
Это выражение позволяет определить оптимальную вы­соту коробчатой балки с моментом инерции 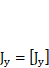и толщиной стенки .Для балки двутаврового сечения с двумя осями симметрии в числителе множитель 6 следует заменить на 12. Отступления от оптимальной высоты в пределах ±20 % приводят к увеличению площади рас­четного сечения примерно на 5 %.

График зависимости площадиА от высоты балки имеет довольно пологий минимум, и все же на начальной стадии проектирования основных несущих элементов не следует пренебрегать аналитическими оценками параметров, по­скольку они дают некоторые исходные значения. В даль­нейшем они могут быть скорректированы из конструктив­ных соображений, но позволят быстрее найти качествен­ный результат. Оптимальная высота ,как правило, по­лучается больше, чем . Может также оказаться, что сечению высотой соответствует недопустимо тонкий пояс. В этом случае следует найти рациональное значение высоты балки в районе 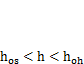,при котором получится разумное сечение пояса и будут выполнены условия прочности и жесткости.

Оптимизация параметров сечения при двух комбинаци­ях нагрузок может быть выполнена численно в среде Mathcad(форма 13.2).

Ездовые балки

Ездовыми называют балки, несущие подвижную нагрузку. Такой нагрузкой могут быть подвесные тали, грузовые или сбрасывающие тележки, вагонетки и пр. Особенность проектирования ездовых балок связана с обеспечением прочности и долговечности узла, воспринимающего мест­ное давление от ходовых колес. Это объясняется тем, что, во-первых, в таком узле возникает дополнительное мест­ное поле напряжений, а во-вторых, количество циклов из­менения этих напряжений за срок службы конструкции обычно превышает количество циклов работы машины, так как за один цикл работы через сечение балки прохо­дит несколько колес и не один раз.

В основном используют три типа ездовых балок. Балки с катанием по нижнему поясу (рис. 13.18, а, б), коробча

тые балки с рельсом посередине пояса (рис. 13.18, в) и балки с рельсом над стенкой, коробчатые или двутавро­вые (рис. 13.18, г, д). Общая компоновка балки произво­дится на основании результатов расчета на прочность и жесткость от общего изгиба. Дополнительные расчеты на прочность и сопротивление усталости производятся для узлов, воспринимающих местные нагрузки от колес.